解方程
求方程的解的過程
使方程左右兩邊相等的未知數的值,叫做方程的解。求方程的解的過程叫做解方程。必須含有未知數等式的等式才叫方程。等式不一定是方程,方程一定是等式。
1.含有未知數的等式叫方程,也可以說是含有未知數的等式是方程。
2.使等式成立的未知數的值,稱為方程的解,或方程的根。
3.解方程就是求出方程中所有未知數的值的過程。
4.方程一定是等式,等式不一定是方程。不含未知數的等式不是方程。
5.驗證:一般解方程之後,需要進行驗證。驗證就是將解得的未知數的值代入原方程,看看方程兩邊是否相等。如果相等,那麼所求得的值就是方程的解。
6.注意事項:寫“解”字,等號對齊,檢驗。
7.方程依靠等式各部分的關係,和加減乘除各部分的關係(加數+加數=和,和-其中一個加數=另一個加數,差+減數=被減數,被減數-減數=差,被減數-差=減數,因數×因數=積,積÷一個因數=另一個因數,被除數÷除數=商,被除數÷商=除數,商×除數=被除數)
⒈估演演算法:剛學解方程時的入門方法。直接估計方程的解,然後代入原方程驗證。
⒉應用等式的性質進行解方程。
⒊合併同類項:使方程變形為單項式
⒋移項:將含未知數的項移到左邊,常數項移到右邊
例如:
解:
⒌去括弧:運用去括弧法則,將方程中的括弧去掉。
解:
6.公式法:有一些方程,已經研究出解的一般形式,成為固定的公式,可以直接利用公式。可解的多元高次的方程一般都有公式可循。
7.函數圖像法:利用方程的解為兩個以上關聯函數圖像的交點的幾何意義求解。
方程是正向思維。
⑴有分母先去分母
⑵有括弧就去括弧
⑶需要移項就進行移項
⑷合併同類項
⑸係數化為1求得未知數的值
⑹開頭要寫“解”
例如:
解:
——————————
解:
——————————
(只取π小數點后兩位)
解這道題首先要知道等於幾,,只取3.14,
解:
不過,不一定放在方程左邊,或一個方程式子里有兩個,這樣就要用數學中的簡便計算方法去解決它了。有些式子右邊有,為了簡便算,可以調換位置。
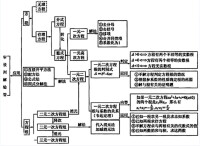
一元二次方程
⒈直接開平方法:直接開平方法就是用直接開平方求解一元二次方程的方法。
用直接開平方法解形如的方程,其解為.
例1.解方程⑴⑵
分析:⑴此方程顯然用直接開平方法好做,⑵方程左邊是完全平方式,右邊=11>0,所以此方程也可用直接開平方法解。
⑴解:∴∴∴∴
⑵解:;∴∴∴∴原方程的解為,
2.配方法:用配方法解方程
先將常數c移到方程右邊:
將二次項係數化為1:
方程兩邊分別加上一次項係數的一半的平方:
方程左邊成為一個完全平方式:;
當時,;
∴(這就是求根公式)
例2.用配方法解方程
解:將常數項移到方程右邊
將二次項係數化為1:
方程兩邊都加上一次項係數一半的平方:
配方:
直接開平方得:
∴
∴原方程的解為,.
3.公式法:把一元二次方程化成一般形式,然後計算判別式的值,當時,把各項係數a,b,c的值代入求根公式就可得到方程的根。
例3.用公式法解方程
解:將方程化為一般形式:∴,,∴∴原方程的解為x?=,x?=.
4.因式分解法:把方程變形為一邊是零,把另一邊的二次三項式分解成兩個一次因式的積的形式,讓兩個一次因式分別等於零,得到兩個一元一次方程,解這兩個一元一次方程所得到的根,就是原方程的兩個根。這種解一元二次方程的方法叫做因式分解法。
例4.用因式分解法解下列方程:
⑴⑵⑶(選學)⑷(選學)
⑴解:化簡整理得(方程左邊為二次三項式,右邊為零)(方程左邊分解因式)∴或(轉化成兩個一元一次方程)∴,是原方程的解。
⑵解:(用提公因式法將方程左邊分解因式)∴或(轉化成兩個一元一次方程)∴,x2=-是原方程的解。注意:有些同學做這種題目時容易丟掉x=0這個解,應記住一元二次方程有兩個解。
⑶解:(十字相乘分解因式時要特別注意符號不要出錯)∴或∴x1=,x2=-是原方程的解。
⑷解:(∵4可分解為2·2,∴此題可用因式分解法)∴,是原方程的解。
小結:一般解一元二次方程,最常用的方法還是因式分解法,在應用因式分解法時,一般要先將方程寫成一般形式,同時應使二次項係數化為正數。
直接開平方法是最基本的方法。
公式法和配方法是最重要的方法。公式法適用於任何一元二次方程(有人稱之為萬能法),在使用公式法時,一定要把原方程化成一般形式,以便確定係數,而且在用公式前應先計算判別式的值,以便判斷方程是否有解。
配方法是推導公式的工具,掌握公式法后就可以直接用公式法解一元二次方程了,所以一般不用配方法解一元二次方程。
就是關於立方的方程
一元三次方程的求根公式用通常的演繹思維是作不出來的,用類似解一元二次方程的求根公式的配方法只能將型如的標準型一元三次方程形式化為的特殊型。
一元三次方程的求解公式的解法只能用歸納思維得到,即根據一元一次方程、一元二次方程及特殊的高次方程的求根公式的形式歸納出一元三次方程的求根公式的形式。歸納出來的形如的一元三次方程的求根公式的形式應該為型,即為兩個開立方之和。歸納出了一元三次方程求根公式的形式,下一步的工作就是求出開立方裡面的內容,也就是用p和q表示A和B。方法如下:
⑴將兩邊同時立方可以得到
⑵
⑶由於,所以⑵可化為
,移項可得
⑷,和一元三次方程和特殊型作比較,可知
⑸,,化簡得
⑹,
⑺這樣其實就將一元三次方程的求根公式化為了一元二次方程的求根公式問題,因為A和B可以看作是一元二次方程的兩個根,而⑹則是關於形如的一元二次方程兩個根的韋達定理,即
⑻,
⑼對比⑹和⑻,可令,,,
⑽由於型為的一元二次方程求根公式為
可化為
⑾
將⑼中的,,,代入⑾可得
⑿
⒀將A,B代入得
⒁
式⒁只是一元三方程的一個實根解,按韋達定理一元三次方程應該有三個根,不過按韋達定理一元三次方程只要求出了其中一個根,另兩個根就容易求出了。
就是x的y次方好複雜的說塔塔利亞發現的一元三次方程的解法一元三次方程的一般形式是
如果作一個橫坐標平移,那麼我們就可以把方程的二次項消去。所以我們只要考慮形如的三次方程。
假設方程的解x可以寫成的形式,這裡a和b是待定的參數。
代入方程,我們就有
整理得到
由二次方程理論可知,一定可以適當選取a和b,使得在的同時,
。這樣上式就成為
兩邊各乘以,就得到
由可知
這是一個關於的二次方程,所以可以解得a。進而可解出b和根x。
一般形式中的三次項。所以只要考慮下面形式的一元四次方程:
關鍵在於要利用參數把等式的兩邊配成完全平方形式。考慮一個參數
a,我們有
等式右邊是完全平方式當且僅當它的判別式為0,即
這是一個關於a的三次方程,利用上面一元三次方程的解法,我們可以
解出參數a。這樣原方程兩邊都是完全平方式,開方后就是一個關於x
的一元二次方程,於是就可以解出原方程的根x。
最後,對於5次及以上的一元高次方程沒有通用的代數解法(即通過各項係數經過有限次四則運算和乘方和開方運算),這稱為阿貝耳定理。
⒈根據問題變未知數
⒉圍繞未知數,尋找問題中的等量關係
⒊利用等量關係列方程
⒋解方程,並作答
