反應級數

在水質自然凈化的機制，探討瞬間反應最著名的研究，是以Michaelis-Menten理論來特定微生物分解的污染質的反應，而微生物分解只有酵素參與。

化學反應的速率方程中各物濃度的指數稱為各物的分級數，所有指數的總和稱為反應總級數，用n表示。如HI合成反應速率方程 為(r為速率，k為速率常數，[ ]代表濃度），表明反應對和的分級數均為1，總級數。反應對級數是由實驗測定的；n可為正、負整數、零或分數。複雜反應，其速率方程不具有簡單的濃度乘積形式者，沒有簡單的級數。

在化學反應的速率方程中，各物濃度項的指數之代數和就稱為該反應的級數(order of reaction)，用n表示。

反應速率方程可表示為:反應速率v速率等於速率常數k與反應物濃度的係數次方的乘積（與生成物無關）。

反應物濃度的次方為該反應物的反應級數或分級數，如反應物A的級數是α，反應物D的級數是β，各反應級數的加和α+β就為該反應的反應級數。反應級數越大，表示濃度對反應速率影響越大。

基元反應 有

故對CO是1級反應；對是1級反應；該反應為2級反應。2級反應k 的量綱：。

（鏈式反應機理）對H2 是1級反應，對 是級反應，反應為級反應。

2級反應——反應速率與反應物濃度無關。

4.4.2 零級反應

反應 A → B 是零級反應有：，得：；

相當於 型直線方程；作c — t曲線，得一直線，其斜率的負值是速率常數k，單位是(L·mol-1 )-1 ·s-1

4.4.3 一級反應

設某個一級反應為：A → B，有，得即，亦相當於型直線方程； lgcA － t呈線性關係，直線斜率為。k 的單位：s-1。

半衰期：即反應進行一半所需的時間。T = t1/2是反應物消耗了一半的時間，稱為反應的半衰期。

當時，對於 ，，稱為半衰期， 可由下式求得：

由得：

即有：

4.4.4 二級反應

A → B為二級反應，有，可得即，亦是型直線方程，作圖，則直線斜率為，截距為，k 的單位：(L·mol-1)1·s-1。

4.4.5 三級反應

A → B為三級反應，有即，得：積分得：，可見呈線性關係。k 單位是(L·mol-1)2·s-1。

可見分別以作圖，圖形呈直線時，分別表示反應是零、一、二、三級反應。

一般而言，基元反應中反應物的級數與其計量係數一致；非基元反應則可能不同，其反應級數都是實驗測定的，而且可能因實驗條件改變而發生變化。例如，蔗糖的水解是二級反應，但是當反應體系中水的量很大時，反應前後體系中水的量可認為未改變，則此反應變現為一級反應。

在不同級數的速率方程中，速率常數k的單位不一樣，一般為L·mol·s，n為反應的反應級數。

基元反應和簡單反應的反應級數n可以是整數一、二、三級（只有少數反應為三級），而複雜反應的反應級數n也可以是分數、負數和零級（光化反應、表面催化反應一般是零級）。負數級表示增加該物質的濃度反而使反應速率下降。但反應速率方程不具有簡單的濃度乘積形式者，反應級數的概念就失去了意義。 

一級反應

定義：凡是反應速率只與物質濃度的一次方成正比者，稱為一級反應（first order reaction）。

五氧化二氮的分解反應：

反應的速率方程為：

可以看出，此反應是一個一級反應。

對上式做定積分，，式中c0是初始濃度，c為反應到t時刻的濃度。

由此可知，當反應物消耗一半時，有

可以看出，一級反應的半衰期與反應的速率常數k成反比，而與反應物的起始濃度無關，這也是一級反應的一個特徵。

二級反應

定義：反應速率和物質濃度的二次方成正比者，稱為二級反應（second order reaction）。

其速率方程：

故對CO是1級反應；對NO2是1級反應；該反應為2級反應。2級反應k的量綱：mol·dm·s。

三級反應

定義：反應速率和物質濃度的三次方成正比者，稱為三級反應（third order reaction）。

三級反應為數不多，在氣相反應中僅知有五個反應是屬於三級反應，而且都與NO有關。這五個反應是：兩個分子的NO和一個分子的，，，，D2反應。即

零級反應

定義：反應速率與物質濃度無關者稱為零級反應（zeroth order reaction）。

反應總級數為零的反應並不多，已知的零級反應中最多的是表面催化反應。例如，氨在金屬鎢上的分解反應：

由於反應只在催化劑表面進行，反應速率只與表面狀態有關。若金屬表面已被吸附的所飽和，再增加NH3的濃度對反應速率不再有影響，此時反應對呈零級反應。

在測定反應級數的實驗中，為了排除產物濃度的干擾，通常是測初速度。為了研究某一反應物濃度與反應速度的函數關係，常常將其他反應物的濃度固定后再確定該反應物的反應級數。

反應級數的測定方法包括兩類：積分法和微分法，前者包括嘗試法、作圖法和半衰期法，後者又包括孤立法。下面介紹作圖法和積分法兩種：

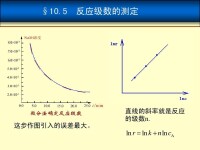
關於微分法。將速率方程取對數 ，則 線性相關，斜率為n。具體步驟為，在曲線上取若干個濃度點，並作切線。計算每點處切線的斜率 ，作 的圖或線性回歸求出n。

關於積分法。積分法是將c~t數據分別已知的動力學方程積分式中，如零級反應是，一級反應是，二級反應等，判斷何者更合適，這種方法需要逐個嘗試，計算量較大 。