冪律分佈
冪律分佈
冪律分佈是指某個具有分佈性質的變數,且其分佈密度函數是冪函數(由於分佈密度函數必然滿足“歸一律”,所以這裡的冪函數,一般規定小於負1)的分佈。
統計物理學家習慣於把服從冪律分佈的現象稱為無標度現象,即,系統中個體的尺度相差懸殊,缺乏一個優選的規模。可以說,凡有生命的地方,有進化,有競爭的地方都會出現不同程度的無標度現象。
自然界與社會生活中存在各種各樣性質迥異的冪律分佈現象,因而對它們的研究具有廣泛而深遠的意義。當樣本數據較多時,變數x的概率密度函數:f(x)~x^(-α-1)。
假設變數x服從參數為 的冪律分佈,則其概率密度函數可以表示為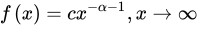
冪律分佈
其互補累積分佈函數(complementary cumulative distribution)為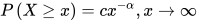
冪律分佈
自然界與社會生活中,許多科學家感興趣的事件往往都有一個典型的規模,個體的尺度在這一特徵尺度附近變化很小。比如說人的身高,中國成年男子的身高絕大多數都在平均值1.70m左右。當然,地域不同這一數值會有一定的變化,但無論怎樣,我們從未在大街上見過身高低於10cm的“小矮人”,或高於10m的“巨人”。如果我們以身高為橫坐標,以取得此身高的人數或概率為縱坐標,可繪出一條鐘形分佈曲線,這種曲線兩邊衰減得極快;類似這樣以一個平均值就能表徵出整個群體特性的分佈,我們稱之為正態分佈。另外一個我們要注意的是最高的人與最矮的人的身高之比,根據吉尼斯世界紀錄,世界上最高的人與最矮的人(均已去世)的身高分別是2. 72m和0. 57m,二者之比為4. 8,這個數值並不是很大,我們將在下文中證實。
對於另一些分佈,像國家GDP或個人收入的分佈,情況就大不一樣了,個體的尺度可以在很寬的範圍內變化,這種波動往往可以跨越多個數量級。比如根據世界銀行的統計,最富有的國家—美國,其2003年GDP高達10,881,609, 000,000美元(一個天文數字),而數據顯示同年GDP最低的國家—西非島國聖多美和普林西比,只有54,000,000美元,二者之比高達201511.3。個人收入分佈亦是如此,想想世界首富比爾·蓋茨那高達465億美元的個人資產就清楚了。國家或城市人口的分佈也會出現類似的情形。據世界銀行的統計, 2003年人口最多的國家—中國,總人口數多達1, 288, 400,000,而數據顯示同年人口最少的國家—西太平洋上的帛琉群島,人口數僅為20,000(不及中國一個普通縣城的人口數),二者之比有64420之多。
以收入值或國家總人口數為橫坐標,以不低於該收入值的人數(概率)或國家數目(概率)為縱坐標,可繪出一條向右偏斜得很厲害,拖著長長“尾巴”的概率分佈曲線,它與鐘形的泊松分佈曲線有顯著的不同。這種“長尾”分佈表明,絕大多數個體的尺度很小,而只有少數個體的尺度相當大,像國家人口,全世界有224個國家和地區,只有11個國家的人口數超過一億。
對“長尾”分佈研究做出重要貢獻的是Zipf和Pareto,雖然他們並不是這種分佈的最早發現者。1932年,哈佛大學的語言學專家Zipf在研究英文單詞出現的頻率時,發現如果把單詞出現的頻率按由大到小的順序排列,則每個單詞出現的頻率與它的排名序號的常數次冪存在簡單的反比關係:
P(r) ~r^-α
這種分佈就稱為Zipf定律,它表明在英語單詞中,只有極少數的詞被經常使用,而絕大多數詞很少被使用。實際上,包括漢語在內的許多國家的語言都有這種特點。物理世界在相當程度上是具有惰性的,動態過程總能找到能量消耗最少的途徑,人類的語言經過千萬年的演化,最終也具有了這種特性,詞頻的差異有助於使用較少的辭彙表達儘可能多的語義,符合“最小努力原則”.分形幾何學的創始人Mandelbrot對Zipf定律進行了修訂,增加了幾個參數,使其更符合實際的情形。
19世紀的義大利經濟學家Pareto研究了個人收入的統計分佈,發現少數人的收入要遠多於大多數人的收入,提出了著名的80/20法則,即20%的人口佔據了80%的社會財富。個人收入X不小於某個特定值x的概率與x的常數次冪亦存在簡單的反比關係:P [X ≥x ]~x - k ,此式即為Pareto定律(帕累托定律)。
Zipf定律與Pareto定律都是簡單的冪函數,我們稱之為冪律分佈;還有其他形式的冪律分佈,像名次-規模分佈、規模-概率分佈,這四種形式在數學上是等價的,其通式可寫成,其中x,y是正的隨機變數,c,r均為大於零的常數. 這種分佈的共性是絕大多數事件的規模很小,而只有少數事件的規模相當大。對上式兩邊取對數,可知lny與lnx滿足線性關係lny=lnc-rlnx,也即在雙對數坐標下,冪律分佈表現為一條斜率為冪指數的負數的直線,這一線性關係是判斷給定的實例中隨機變數是否滿足冪律的依據。
判斷兩個隨機變數是否滿足線性關係,可以求解兩者之間的相關係數;利用一元線性回歸模型和最小二乘法,可得lny對lnx的經驗回歸直線方程,從而得到y與x之間的冪律關係式。在雙對數坐標下的圖形,由於某些因素的影響,前半部分的線性特性並不是很強,而在後半部分,則近乎為一直線,其斜率的負數就是冪指數。
實際上,冪律分佈廣泛存在於物理學、地球與行星科學、計算機科學、生物學、生態學、人口統計學與社會科學、經濟與金融學等眾多領域中,且表現形式多種多樣。
在自然界與日常生活中,包括地震規模大小的分佈(古登堡2里希特定律)、月球表面上月坑直徑的分佈、行星間碎片大小的分佈、太陽耀斑強度的分佈、計算機文件大小的分佈、戰爭規模的分佈、人類語言中單詞頻率的分佈、大多數國家姓氏的分佈、科學家撰寫的論文數的分佈、論文被引用的次數的分佈、網頁被點擊次數的分佈、書籍及唱片的銷售冊數或張數的分佈、每類生物中物種數的分佈、甚至電影所獲得的奧斯卡獎項數的分佈等,都是典型的冪律分佈。
1:股票流通市值的冪分佈:
僅取A股市場的100家股票,按流通市值大小排序,擬合的相關程度99.6%,其冪指數為0.897。
2:A股市場每股收益的冪分佈
1000家股票擬合的冪分佈函數曲線,擬合的相關程度93.7%,其冪指數約為0.53。
3:新疆風城油田的實際數據
抽油機作為耗電“老虎”,其工程指標為產液單耗,即從井每產一噸液耗多少度電,描述抽油機自身效率的技術指標為系統效率。二者的關係呈冪律分佈關係,這一發現對於我們工程技術或油田管理人員進行提高系統效率,無疑具有很大的指導意義:即抓住20%的低效井進行治理改造,就可取得80%的提高效果。
為了解釋冪律分佈的形成原因,科學家們提出了幾種機制,包括增長與優先連接、自組織臨界、HOT理論、滲流模型及一些隨機過程等。
Barabási與Albert針對複雜網路中普遍存在的冪律分佈現象,提出了網路動態演化的BA模型,他們解釋,成長性和優先連接性是無標度網路度分佈呈現冪律的兩個最根本的原因。所謂成長性是指網路節點數的增加,像Internet中自治系統或路由器的添加,以及WWW中網站或網頁的增加等,優先連接性是指新加入的節點總是優先選擇與度值較高的節點相連,比如,新網站總是優先選擇人們經常訪問的網站作為超鏈接。隨著時間的演進,網路會逐漸呈現出一種“富者愈富,貧者愈貧”的現象。社會學家所說的“馬太效應”。“優先連接”並不適用於所有出現冪律分佈的情況,即便是對於某些無標度網路,用它解釋冪律的成因也顯得很不合理。以生態系統中的食物鏈為例,認為被捕食者最有可能被獵物廣泛的雜食性捕食者吃掉,確實是一件很荒唐的事。還有像Internet、航空網等網路,流量或容量的限制可以在一定程度上抑制優先連接性,電影演員的合作網路中,節點(演員)的衰老或隱退也能起到類似的作用。
自組織臨界理論認為,由大量相互作用的成分組成的系統會自然地向自組織臨界態發展;當系統達到這種狀態時,即使是很小的干擾事件也可能引起系統發生一系列災變。
著名的“沙堆模型”形象地說明了自組織臨界態的形成和特點:
設想在一平台上緩緩地添加沙粒,一個沙堆逐漸形成。開始時,由於沙堆平矮,新添加的沙粒落下后不會滑得很遠。但是,隨著沙堆高度的增加,其坡度也不斷增加,沙崩的規模也相應增大,但這些沙崩仍然是局部性的。到一定時候,沙堆的坡度會達到一個臨界值,這時,新添加一粒沙子(代表來自外界的微小干擾)就可能引起小到一粒或數粒沙子,大到涉及整個沙堆表面所有沙粒的沙崩。這時的沙堆系統處於“自組織臨界態”,有趣的是,臨界態時沙崩的大小與其出現的頻率呈冪律關係。
冪律分佈是自組織臨界系統在混沌邊緣,即從穩態過渡到混沌態的一個標誌,利用它可以預測這類系統的相位及相變。自組織臨界理論可以解釋諸如火山爆發、山體滑坡、岩層形成、日輝耀斑、物種滅絕、交通阻塞、以及金融市場中泡沫崩潰的冪律分佈現象。這種理論的啟示是小事件和大事件可能有相同的起因,這為地震、恐龍滅絕、森林火災等複雜大系統的突變提供了新的解釋。以恐龍滅絕為例,古生物學家經過對化石的研究指出,這一重大事件不是經歷了數萬年或者幾年,而是在20多天的突變中“一朝覆滅”的。恐龍的滅絕可以被看作是處於臨界狀態下的生態系統發生的一次“大雪崩”
另一種解釋冪律分佈形成原因的重要理論是HOT。該理論由加州大學聖巴巴拉分校的Jean Carlson以及加州理工學院的John Doyle提出。他們宣稱,對於由許多子系統連結成的複雜系統,不管是自然演化還是人為設計的,當該系統可以有效地容忍某些不確定因素時(具強健性),將對其他未被考慮到的不確定因素變得更敏感。也就是說,強健性和敏感度具有相互遞換的效果。這裡的不確定因素包含系統內部的不確定因素以及外在環境的干擾。以生態系統為例,如果它可以容忍氣溫、濕度、養分等巨幅變化,那麼這生態系統卻可能無法容忍一些意料之外的小干擾,如基因突變、外來族群遷入、或新的病毒,這些干擾可能會造成生態環境的巨大改變。當一複雜系統處於HOT狀態時,該系統將滿足冪律,也就是說,全局性的優化過程可導致冪律分佈:具有特徵尺度的輸入經過一個全局性的系統“產量”優化過程后,可產生具有冪律分佈特性的輸出。全局性優化在生態系統、航空航天與汽車系統、林業系統、網際網路、交通運輸及電力系統中具有廣泛的應用,HOT理論可以解釋上述系統中出現的冪律分佈現象,比如可以解釋林業系統中火災規模所呈現的冪律分佈。
