graph theory
graph theory
graph theory
中文名:圖論
圖論:英文名:Graph Theory,它是數學的一個分支。它以圖為研究對象。圖論中的圖是由若干給定的點及連接兩點的線所構成的圖形,這種圖形通常用來描述某些事物之間的某種特定關係,用點代表事物,用連接兩點的線表示相應兩個事物間具有某種關係。
圖論本身是應用數學的一部分,因此,歷史上圖論曾經被好多位數學家各自獨立地建立起來。
關於圖論的文字記載最早出現在歐拉1736年的論著中,他所考慮的原始問題有很強的實際背景。後來,德國自然科學家基希霍夫對於電網路的研究導致他發現了圖論的基本概念和定理;英國數學家凱萊為了計數有機化學中的同分異構而考慮到樹;英國數學家哈密頓提出了一個與圖論有關的難題;不久又出現了著名的四色猜想,這些工作都促進了圖論的產生和發展。在20世紀內,圖論中又有大量的新發現,並被應用到許多領域。
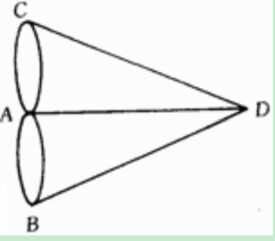
圖論起源於著名的柯尼斯堡七橋的問題。18世紀,在柯尼斯堡的普萊格爾河上有七座橋將河中的島及島與河岸連接起來,如圖1所示,表示陸地:問題是要從這四塊陸地中任何一塊開始,通過每一座橋正好一次,再回到起點。然而無數次的嘗試都沒有成功。歐拉在1736年解決了這個問題,他用抽象分析法將這個問題化為第一個圖論問題,即把每一塊陸地用一個點來代替,將每一座橋用連接相應的兩個點的一條線來代替,從而相當於得到一個“圖”(如圖2),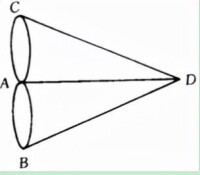 歐拉證明了這個問題沒有解,並且推廣了這個問題,給出了對於一個給定的圖可以按某種方式走遍(即一筆畫)的判定法則。這項工作使歐拉成為圖論(及拓撲學)的創始人。
歐拉證明了這個問題沒有解,並且推廣了這個問題,給出了對於一個給定的圖可以按某種方式走遍(即一筆畫)的判定法則。這項工作使歐拉成為圖論(及拓撲學)的創始人。

graph theory
1847年,德國學者基希霍夫在研究物理問題時建立了樹的理論。他用一類線性方程組來描述一個電網路的每一條支路中和環繞每一個迴路的電流。他像數學家一樣抽象地思考問題:用一個只由點和線組成的相應的組合結構來代替原來的電網路,而並不指明每條線所代表的電器元件的種類。事實上,他把每個電網路用一個基本圖來代替。為了解相應的方程組,他用一種結構方法指出,只要考慮一個圖的任何一個“生成樹”所決定的那些獨立圈就夠了。他的方法現已成為圖論中的標準方法。
圖3表示一個電網路N及基希霍夫為它設計的基本圖G和一個生成樹T。
1857年,英國數學家凱萊從事計數有給定的碳原子數n的飽和碳氫化合物 的同分異構物(如圖4所示)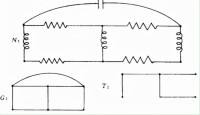 ,獨立地提出了樹的概念。凱萊把這個問題抽象地敘述為:求有P個點的樹的數目,其中每個點的度等於1或4,樹上的點對應一個氫原子或一個碳原子。凱萊的工作是圖的計數理論的起源。法國數學家若爾當在1869年作為一個純數學對象獨立地發現了樹,他並不知道樹與現代的化學學說有關。
,獨立地提出了樹的概念。凱萊把這個問題抽象地敘述為:求有P個點的樹的數目,其中每個點的度等於1或4,樹上的點對應一個氫原子或一個碳原子。凱萊的工作是圖的計數理論的起源。法國數學家若爾當在1869年作為一個純數學對象獨立地發現了樹,他並不知道樹與現代的化學學說有關。

graph theory
graph theory
1859年,英國數學家哈密頓發明了一種遊戲:用一個規則的實心十二面體,它的20個頂點標出世界著名的20個城市,要求遊戲者找一條沿著各邊通過每個頂點剛好一次的閉迴路,即“繞行世界”一周,如圖5所示。用圖論的語言來說,遊戲的目的是在十二面體的圖中找出一個生成圈。這個問題後來就叫做哈密頓問題。由於運籌學、計算機科學和編碼理論中的很多問題都可以化為哈密頓問題,從而引起廣泛的注意和研究。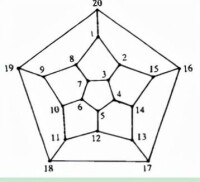

graph theory
在圖論的歷史中,還有一個最著名的問題——四色猜想。這個猜想說,在一個平面或球面上的任何地圖能夠只用四種顏色來著色,使得沒有兩個相鄰的國家有相同的顏色。每個國家必須由一個單連通域構成,而兩個國家相鄰是指它們有一段公共的邊界,而不僅僅只有一個公共點。四色猜想有一段有趣的歷史(見四色問題)。每個地圖可以導出一個圖,其中國家都是點,當相應的兩個國家相鄰時這兩個點用一條線來連接。所以四色猜想是圖論中的一個問題。它對圖的著色理論、平面圖理論、代數拓撲圖論等分支的發展起到推動作用。
20世紀以來,圖論不斷地發展和完善,並獲得廣泛的應用。1936年,德國社會心理學家萊溫把圖論應用於心理學研究。他提出,一個人的“生活空間”可以用一張平面地圖來代表,其中各個區域代表一個人的各種活動。他所處理的實際上是圖,其觀點影響了當時的一批心理學家。他們提出了圖的一種心理學解釋,其中點代表人,而線代表人與人之間的關係,括愛、恨、交往與支配等。他們對圖論有一些獨到的發現。1960年,荷蘭—美國物理學家烏倫貝克用圖論來研究統計力學,他以點來代表分子,兩個點間的連線表示分子間的相互作用。在楊振寧和李政道的工作中也有類似的解釋,他們以點表示歐氏空間中的小立方體,每一個立方體可能被一個分子佔有或不被分子佔有,兩個點的連線則表示兩個空間都被佔有。圖論還被應用於概率論中的馬爾可夫鏈的研究。例如,南斯拉夫—美國數學家弗勒引進了有向圖:點代表事件,有向線表示兩個事件直接相繼有正的概率;有向圖的一種類似的表示法還出現在數值分析的矩陣求逆和特徵值計算之中,美國數學家瓦爾加在1962年建立的一種對方陣構造有向圖的方法與處理馬爾可夫鏈的方法相類似。在線性規劃和運籌學的各領域中,也利用圖論的方法來研究網路上流的形式,1962年以來已有許多工作。在純粹數學中,圖論被用來研究拓撲學中的單純復形,美國數學家維布倫在20世紀20-30年代就做出了先驅性的貢獻。他把一個圖定義為維數等於1或0的一個復形,1維單形是一條線,只由點組成的復形是0維的。除了這些特殊情形外,每一個圖都是一個1維復形。正因為這個原因,在1936年出現的第一本圖論的書(柯尼希著)的副標題是“線復形的組合拓撲學”。
書 名:
1.圖論 Graph theory 第3版
作 者: (德)迪斯特爾 著
出 版 社:世界圖書出版公司
出版時間: 2008-3-1 字 數:版次: 1 頁 數: 410 印刷時間: 2008-3-1 開 本: 16開 印次: 1 紙 張:膠版紙
I S B N : 9787506291859
所屬分類:圖書 >> 自然科學 >> 數學 >> 代數 數論 組合理論
內容簡介:Many authors begin their preface by confidently describing how their book arose. We started this project so long ago, and our memories are so weak, that we could not do this truthfully. Others begin by stating why they decided to write. Thanks to Freud, we know that unconscious reasons can be as important as conscious ones, and so this seems impossible, too. Moreover, the real question that should be addressed is why the reader should struggle with this text.
2.代數圖論:
作者:Chris Godsi Gordon Royle
·出版社:世界圖書出版公司
·頁碼:439 頁
·出版日期:2004年04月
·ISBN:7506266180
·條形碼:9787506266185
·版本:第1版
·裝幀:平裝
·開本:24開 Pages Per Sheet
3.圖論及其應用 J.A.邦迪 U.S.R.