濾子基
濾子基
濾子基(filter base)生成濾子的一類集族。
在數學中,濾子是偏序集合的特殊子集。經常使用的特殊情況是:要考慮的有序集合只是某個集合的冪集,並用集合包含來排序。濾子出現在序理論和格理論中,還可以在它們所起源的拓撲學中找到。濾子的對偶概念是理想。
濾子是昂利·嘉當在1937年發明的並隨後在尼古拉·布爾巴基的書《Topologie Générale》中作為對E. H. Moore和H. L. Smith在1922年發明的網的概念的替代。
濾子和 濾子基的最一般的形式是定義在一般的偏序集上的。
偏序集合 (P,≤)的子集F稱為 濾子基,若F滿足:
• F非空。
• ∀x, y ∈ F,∃z ∈ F,使z ≤ x且z ≤ y。
若F同時還滿足:
• F是上閉的:∀x ∈ F,y ∈ P,x ≤ y ⇒ y ∈ F。
則稱F是 濾子。
偏序集P的濾子F稱為 真濾子,若F≠P。
濾子基
濾子基
濾子基
濾子基
濾子基
包含給定元素 的最小的濾子是 主濾子。稱為該濾子的 主元素。的主濾子是:給出,並記為。
濾子的序對偶(交換≥和≤,∧和∨)概念是理想;由於濾子和理想在概念上的序對偶性,關於濾子的討論通常可以與理想的討論相關聯。關於濾子的其它信息(如 極大濾子,素濾子)參見理想。關於 超濾子有專門的條目。
濾子最初只是為格定義的。在這種情況下,濾子可以被特徵化為如下等價陳述:
格 (P,≤)的非空子集F是濾子,當且僅當它是對有限交(下確界)運算封閉的上閉集合。
即,對於所有在F中的x,y,x∧y也在F中。
濾子的一個特殊情況是定義在集合上的濾子。假定一個集合S,偏序⊆可以通過子集包含定義在冪集 P(S)上,把 ( P(S),⊆)變成了一個格。定義S上的 濾子F為 P(S)的有如下性質的子集:
1.S∈F(F非空)
2.∅ ∉F(F為真子集)
3.若A∈F且B∈F,則A∩B∈F(F對有限交封閉)
4.若A∈F且A⊆B,則B∈F中,對於所有B⊆S。(F是上閉集合)
前三個性質蘊涵了 集合上的濾子有有限交集性質。通過這個定義在集合上的濾子是真濾子。為此有時叫做 集合上的真濾子;但是,只要集合上下文是明顯的,短名字就足夠了。
濾子基是 P(S)的帶有如下性質的子集B:
1.B的任何兩個集合的交集包含B的一個集合
2.B是非空的並且空集不在B中
濾子基B可以通過把包含B的一個集合的 P(S)的所有集合包括在內而變成(真)濾子。所以結果的濾子基經常被稱為是生成或擴張自濾子基B。所有濾子更加是濾子基,所以經過濾子基到濾子的過程可以被看做某種補全。
如果B和C是在S上的兩個濾子基,要說C細於(finer than)B(或者C是B的精細),意味著對於每個B∈B,有一個C∈C使得C⊆B。
• 對於濾子基B和C,如果B細於C且C細於B,則B和C被稱為等價濾子基。
• 對於濾子基A,B和C,如果A細於B且B細於C,則A細於C。
給定 P(S)的一個子集T,我們可以問是否存在一個最小的濾子F包含T。這樣一個濾子存在,當且僅當T的子集的有限交集是非空的。我們稱T為F的 子基,並稱F生成自T。F可以通過採納T的所有有限交集來構造,它就是F的濾子基。
• 最簡單的濾子的例子是包括S的一個特定非空子集C的S的所有子集的集合。這種濾子叫做C生成的主濾子。
• 在無限集合S上Frechet濾子是S的有有限補元的所有子集的集合。
• 在集合X上的一致空間是在X×X上的濾子。
• 可以使用Rasiowa-Sikorski引理建立在偏序集合內的濾子,這經常用於力迫。
濾子基
濾子基
濾子基
濾子基
集合 被叫做自然數序列 的尾濾子基。尾濾子基由任何網使用構造 得到。所以,所有的網都生成一個濾子基(並因此是濾子)。因為所有序列都是網,這對所有序列也成立。
對於在集合S上的任何濾子F,如下定義的集合函數
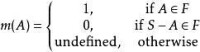
濾子基
濾子基
在拓撲學和數學分析中,濾子被用來定義收斂,類似於序列在度量空間空間中所扮演的角色。
一個序列通常用作為全序集合來索引。因此,在第一可數空間中的極限可以被序列所描述。但是如果,空間不是第一可數的,則必須使用網或濾子。網推廣了序列的概念,通過簡單的要求索引集合是有向集合。濾子可以被認為是從多個網建立的集合。因為,濾子的極限和網的極限二者在概念上同於序列的極限。
使用濾子的好處是很多結果的證明可以不使用選擇公理。
鄰域基
選取拓撲空間T和一個點x∈T。
• 選取N是在T的點x上的鄰域濾子。這意味著N是點x的所有拓撲鄰域的集合。可以驗證N是個濾子。鄰域系統是鄰域濾子的另一個名字。
• 要說N是在T的x上的鄰域基,就意味著對於所有V∈N,存在N∈N使得N⊆V。注意所有鄰域基都是濾子基。
收斂濾子基
選取拓撲空間T和一個點x∈T。
• 要說濾子基B收斂到x,指示為B→x,就意味著對於所有x的鄰域U,有B∈B使得B⊆U。在這種情況下,x叫做B的極限點而B叫做收斂濾子基。注意這裡用的術語“極限點”是“極限”概念到濾子基的推廣;在某些上下文中,術語“極限點”用於下面解說的簇點,並以此區別於術語“極限”。
• 對於所有x的鄰域基N,有N→x。
• 如果N是p的鄰域基而C是在T上的濾子基,則C→x當且僅當C細於N。
• 對於X⊆T,要說p是X在T中極限點,就意味著對於T中的p的每個鄰域U,有U∩(A- {p})≠∅。
• 對於X⊆T,p是X在T中的極限點,當且僅當存在在A- {p}上的濾子基B使得B→p。
聚集
選取拓撲空間T和點x∈T。
• 要說x是B在T上的聚集點,就意味著對於每個B∈B和對於x在T中的每個鄰域U,有B∩U≠∅。在這種情況下,B被被稱為聚集於點x。
• B的下極限是B的所有聚集點的集合的下確界。
• B的上極限是B的所有聚集點的集合的上確界。
• B是收斂濾子基,當且僅當它的下極限和上極限一致;在這種情況下它們所一致於的值是這個濾子基的極限。
• 對於濾子基B使得B→x,極限點x也是聚集點。
• 對於濾子基B有著聚集點x,x不必然是極限點。
• 對於濾子基B聚集於點x,有一個濾子基C細於會聚到x的濾子基B。
• 對於濾子基B,集合∩{cl(B):B∈B}是所有B的聚集點的集合(注意:cl(B)是B的閉包)。假定T是偏序集合。
拓撲空間的性質
選取拓撲空間T。
• T是豪斯多夫空間,當且僅當對於所有在T上的濾子基B,B→p並且B→q蘊涵p=q(就是說,所有濾子(基)有最多一個極限點)。
• T是緊緻空間,當且僅當所有在X上的濾子基聚集。
• T是緊緻空間,當且僅當所有在X上的濾子基是收斂濾子基的子集。
• T是緊緻空間,當且僅當所有在X上的超濾子會聚。
拓撲空間上的函數
濾子基
濾子基
選取拓撲空間X和Y和子集E⊆X。選取E上的濾子基B和函數。B在f下的像f[B]是集合。像f[B]形成了在Y上的濾子基。
濾子基
濾子基
f連續於x,當且僅當 蘊涵。
選取度量空間X帶有度量d。
• 要說濾子基B在X上是柯西的,就意味著對於每個實數ε>0,有B∈B使得B的度量直徑小於ε。
• 選取 (x)是度量空間X中的序列。(x)是柯西序列,當且僅當形如{ {x,x,...}:n∈ {1,2,3,...} }的濾子基是柯西的 [2]。
濾子基
濾子基
濾子基
濾子基
給定一致空間X,在X上的濾子F被稱為 柯西濾子,如果對於所有周圍(entourage)U,有著 帶有 對於所有。在度量空間中,這選取形式 F為柯西的,如果對於所有。X被稱為是完備的,如果所有柯西濾子會聚。反過來說,在一致空間上所有收斂濾子是柯西濾子。此外,所有柯西濾子的聚集點是極限點。
緊緻一致空間是完備的:在緊緻空間中每個濾子都有聚集點,並且如果濾子是柯西的,這種聚集點就是極限點。進一步的,一致空間是緊緻的當且僅當它是完備的和完全有界的。