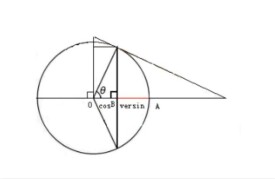
正矢

現在基本不用的三角函數中一種。

歷史上用過下面兩個函數: 正矢 余矢 。

三角函數（trigonometric function），亦稱圓函數，是正弦、餘弦、正切、餘切、正割、餘割等函數的總稱。在平面上直角坐標系Oxy中，與x軸正向夾角為α的動徑上取點P，P的坐標是，則正弦函數，餘弦函數正切函數，餘切函數，正割函數，餘割函數。歷史上還用過正矢函數，余矢函數等等。

這8種函數在1631年徐光啟等人編譯的《大測》中已齊備。正弦最早被看作圓內圓心角所對的弦長，公元前2世紀古希臘天文學家希帕霍斯就製造過這種弦表，公元2世紀托勒密又造了0°～90°每隔半度的正弦表。5世紀時印度最早引入正弦概念，還給出正弦函數表，記載於《蘇利耶曆數書》（約400年）中。該書還出現了正矢函數，現在已很少使用它了。約510年印度數學家阿那波多考慮了餘弦概念，傳到歐洲後有多種名稱，17世紀后才統一。正切和餘切函數是由日影的測量而引起的，9世紀的阿拉伯計算家哈巴什首次編製了一個正切、餘切表。10世紀的艾布·瓦法又單獨編製了第一個正切表。哈巴什還首先提出正割和餘割概念，艾布·瓦法正式使用。到1551年奧地利數學家、天文學家雷蒂庫斯在《三角學準則》中收入正弦、餘弦、正切、餘切、正割、餘割6種函數，並附有正割表。他還首次用直角三角形的邊長之比定義三角函數。1748年歐拉第一次以函數線與半徑的比值定義三角函數，令圓半徑為1，並創用許多三角函數符號。至此現代形式的三角函數開始通行，並不斷發展至今。

正矢函數y關於θ正矢值的函數

余矢函數y關於θ余矢值的函數