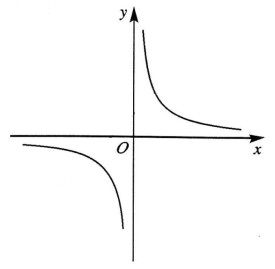
雙曲正弦函數

雙曲函數（hyperbolic function）可藉助指數函數定義Sinh_cosh_tanh雙曲正弦

sh z=(e^z-e^(-z))/2⑴

雙曲餘弦

ch z=(e^z+e^(-z))/2⑵

雙曲正切

th z=sh z/ch z=(e^z-e^(-z))/(e^z+e^(-z))⑶

雙曲餘切

cth z=ch z/sh z=(e^z+e^(-z))/(e^z-e^(-z))⑷

雙曲正割

sch z=1/ch z⑸

雙曲餘割

xh(z)=1/sh z⑹

其中，指數函數（exponentialCsch_sech_cothfunction）可由無窮級數定義

e^z=1+z/1！+z^2/2！+z^3/3！+z^4/4！+…+z^n/n！+…⑺

雙曲函數的反函數（inverse hyperbolic function）分別記為ar sh z、ar ch z、ar th z等。

在數學中，雙曲函數類似於常見的三角函數（也叫圓函數）。基本雙曲函數是雙曲正弦“sinh”，雙曲餘弦“cosh”，從它們導出雙曲正切“tanh”等。也類似於三角函數的推導。反函數是反雙曲正弦“arsinh”（也叫做“arcsinh”或“asinh”）以此類推。

雙曲函數出現於某些重要的線性微分方程的解中，譬如說定義懸鏈線和拉普拉斯方程。

雙曲函數接受實數值作為叫做雙曲角的自變數。在複分析中，它們簡單的是指數函數的有理函數，並因此是完整的。射線出原點交雙曲線x^2-y^2=1於點(cosh a,sinh a），這裡的a被稱為雙曲角，是這條射線、它關於x軸的鏡像和雙曲線之間的面積。定義

雙曲函數（Hyperbolic Function）包括下列六種函數：

sinh/雙曲正弦：sinh(x)=[e^x-e^(-x)]/2

cosh/雙曲餘弦：cosh(x)=[e^x+e^(-x)]/2

tanh/雙曲正切：tanh(x)=sinh(x)/cosh(x)=[e^x-e^(-x)]/[e^x+e^(-x)]

coth/雙曲餘切：coth(x)=cosh(x)/sinh(x)=[e^x+e^(-x)]/[e^(x)-e^(-x)]

sech/雙曲正割：sech(x)=1/cosh(x)=2/[e^x+e^(-x)]

csch/雙曲餘割：csch(x)=1/sinh(x)=2/[e^x-e^(-x)]

其中，

e是自然對數的底

e≈2.71828 18284 59045...=1/0!+1/1!+1/2!+1/3!+1/4!+1/5!...+1/n!+...

e^x表示e的x次冪，展開成無窮冪級數是：

e^x=x^0/0!+x^1/1!+x^2/2!+x^3/3!+x^4/4!+x^5/5!...+x^n/n!+...

如同點(cost,sint)定義一個圓，點(cosh t,sinh t)定義了右半直角雙曲線x^2 y^2=1。這基於了很容易驗證的恆等式

cosh^2(t)-sinh^2(t)=1

和性質t>0對於所有的t。

參數t不是圓角而是雙曲角，它表示在x軸和連接原點和雙曲線上的點(cosh t,sinh t)的直線之間的面積的兩倍。

函數cosh x是關於y軸對稱的偶函數。

函數sinh x是奇函數，就是說-sinh x=sinh(-x)且sinh 0=0。

實變雙曲函數

y=sh(x).定義域：R.值域：R.奇函數。函數圖像為過原點並且穿越Ⅰ，Ⅲ象限的嚴格單調遞增曲線，當x->+∞時是（1/2）e^x的等價無窮大。函數圖像關於原點對稱。

y=ch(x).定義域：R.值域：[1,+∞）.偶函數。函數圖像是懸鏈線，最低點是（0,1），在Ⅰ象限部分是嚴格單調遞增曲線，當x->+∞時是（1/2）e^x的等價無窮大。函數圖像關於y軸對稱。

y=th(x).定義域：R.值域：（-1,1）.奇函數。函數圖像為過原點並且穿越Ⅰ，Ⅲ象限的嚴格單調遞增曲線。其圖像被限制在兩漸近線y=1和y=-1之間.lim[x->+∞，tanh(x)=1],lim[x->-∞，tanh(x)=-1]。

y=cth(x).定義域：{x|x≠0}.值域：{x||x|>1}.奇函數。

y=sch(x).定義域：R.值域：（0,1].偶函數。最高點是（0,1），函數在（0,+∞）嚴格單調遞減.x軸是其漸近線.lim[x->；∞，sech(x)]=0.

y=xh(x).定義域：{x|x≠0}.值域：{x|x≠0}.奇函數。函數圖像分為兩支，分別在Ⅰ，Ⅲ象限，函數在（-∞，0）和（0，+∞）分別單調遞減。垂直漸近線為y軸，兩水平漸近線為x軸.lim[x->；∞，csch(x)]=0.

雙曲函數名稱的變更：sh也叫sinh,ch也叫cosh,th也叫tanh，cth也叫coth，sch也叫sech，xh也叫csch。

定義

雙曲正弦：sh(z)=[e^z-e^(-z)]/2

雙曲餘弦：ch(z)=[e^z+e^(-z)]/2

性質

解析性：shz,chz是全平面的解析函數

周期性：shz,chz是周期函數，周期為2πi，這是完全不同於實變函數中的性質

反雙曲函數是雙曲函數的反函數。它們的定義為：

arcsh(x)=ln[x+sqrt(x^2+1）]

arcch(x)=ln[x+sqrt(x^2-1）]

arcth(x)=ln[sqrt（1-x^2）/（1-x)]=ln[（1+x)/（1-x)]/2

arccth(x)=ln[sqrt(x^2-1）/(x-1）]=ln[(x+1）/(x-1）]/2

arcsch(x)=±ln[1+sqrt（1-x^2）/x]

arcxh(x)=ln[1-sqrt（1+x^2）/x]，如果x<0

ln[1+sqrt（1+x^2）/x]，如果x>0

其中，

sqrt為square root的縮寫，即平方根

雙曲函數與三角函數有如下的關係：

*sinh x=-i*sin(i*x)

*cosh x=cos(i*x)

*tanh x=-i*tan(i*x)

*coth x=i*cot(i*x)

*sech x=sec(i*x)

*csch x=i*csc(i*x)

i為虛數單位，即i*i=-1

與雙曲函數有關的恆等式如下：

ch^2(x)-sh^2(x)=1

cth^2(x)-xh^2(x)=1

th^2(x)+sch^2(x)=1

加法公式

sinh(x+y)=sinh(x)*cosh(y)+cosh(x)*sinh(y)

cosh(x+y)=cosh(x)*cosh(y)+sinh(x)*sinh(y)

tanh(x+y)=[tanh(x)+tanh(y)]/[1+tanh(x)*tanh(y)]

coth(x+y)=（1+coth(x)*coth(y))/(coth(x)+coth(y))

減法公式

sinh(x-y)=sinh(x)*cosh(y)-cosh(x)*sinh(y)

cosh(x-y)=cosh(x)*cosh(y)-sinh(x)*sinh(y)

tanh(x-y)=[tanh(x)-tanh(y)]/[1-tanh(x)*tanh(y)]

coth(x-y)=（1-coth(x)*coth(y))/(coth(x)-coth(y))

二倍角公式

sinh（2x)=2*sinh(x)*cosh(x)

cosh（2x)=cosh^2(x)+sinh^2(x)=2*cosh^2(x)-1=2*sinh^2(x)+1

tanh（2x)=2tanh(x)/（1+tanh^2(x))

coth（2x)=（1+coth^2(x))/2coth(x)

三倍角公式

sinh（3x)=3sinh(x)+4sinh^3(x)

cosh（3x)=4cosh^3(x)-3cosh(x)

半形公式

cosh^2(x/2）=(cosh(x)+1）/2

sinh^2(x/2）=(cosh(x)-1）/2

tanh(x/2）=(cosh(x)-1）/sinh(x)=sinh(x)/(cosh(x)+1）

coth(x/2）=sinh(x)/(coth(x)-1）=(coth(x)+1）/sinh(x)

德莫佛公式

（cosh(x）±sinh(x))^n=cosh(nx)±sinh(nx)

雙曲函數的恆等式都在圓三角函數有相應的公式。Osborn's rule指出：將圓三角函數恆等式中，圓函數轉成相應的雙曲函數，有兩個sinh的積時（包括coth^2(x),tanh^2(x),csch^2(x),sinh(x)*sinh(y））則轉換正負號，則可得到相應的雙曲函數恆等式。如

三倍角公式

sin（3*x)=3*sin(x)+4*sin^3(x)

sinh（3*x)=3*sinh(x)+4*sinh^3(x)

雙曲正弦函數在是凸函數，在是凹函數

證明：根據函數凹凸性的判定定理：設f(x)在[a,b]上連續，在(a,b)內具有一階和二階導數，那麼：

（1）若在（a,b）內，，則f(x)在[a,b]上的圖形是凹的

（2）若在（a,b）內，，則f(x)在[a,b]上的圖形是凸的

根據雙曲函數的導數公式，求得雙曲正弦函數的二階導數 為：

可見，雙曲正弦函數的二階導數仍然是雙曲正弦函數（它本身），而根據雙曲正弦函數的單調性，且sinh0=0。可知當x>0時，sinhx的二階導數大於0。x<0時，sinhx的二階導數小於0，則可得出上述結論。

（sinh(x))'=cosh(x)

（cosh(x))'=sinh(x)

（tanh(x))'=sech^2(x)

（coth(x))'=-csch^2(x)

（sech(x))'=sech(x)tanh(x)

（csch(x))'=-csch(x)coth(x)

（arcsinh(x))'=1/sqrt(x^2+1）

（arccosh(x))'=1/sqrt(x^2-1）(x>1）

（arctanh(x))'=1/（1-x^2）(|x|<1）

（arccoth(x))'=1/（1-x^2）(|x|>1）

∫sinh(x)dx=cosh(x)+c

∫cosh(x)dx=sinh(x)+c

∫sech^2(x)dx=tanh(x)+c

∫csch^2(x)dx=-coth(x)+c

∫sech(x)tanh(x)dx=-sech(x)+c

∫csch(x)coth(x)dx=-csch(x)+c

∫tanh(x)dx=ln(cosh(x))+c

∫coth(x)dx=ln|sinh(x)|+c

∫sech(x)dx=arctan(sinh(x))+c=2arctan(e^x)+c1=2arctan(tanh(x/2））+c2

∫csch(x)dx=ln|coth(x)-csch(x)+c=ln|tanh(x/2）|+c

∫[1/sqrt(x^2+1）]dx=arcsinh(x)+c=ln(x+sqrt(x^2+1））+c

∫[1/sqrt(x^2-1）]dx=sgn(x)arccosh|x|+c=ln|x+sqrt(x^2-1）|+c

（sgn是符號函數.sgn(x)=x/|x|,x≠0;sgn(x)=0,x=0)

sinh(z)=z+z^3/3!+z^5/5!+z^7/7!+...+z^（2k-1）/（2k-1）！+... (z∈C)

cosh(z)=1+z^2/2!+z^4/4!+z^6/6!+...+z^（2k)/（2k)!+... (z∈C)

arcsinh(z)=z-（1/6）z^3+（3/40）z^5-（5/112）z^7+...+(-1）^k[（2k-1）！！/（2k)!!][z^（2k+1）/（2k+1）]+... (|z|<1）

arctanh(z)=z+z^3/3+z^5/5+z^7/7+...+z^（2k-1）/（2k-1）+... (|z|<1）

雙曲函數並非單純是數學家頭腦中的抽象，在物理學眾多領域可找到豐富的實際應用實例。

阻尼落體

在空氣中由靜止開始下落的小石塊既受重力的作用又受到阻力的作用。設小石塊的質量為m，速度為v，重力加速度為g，所受空氣阻力假定與v2正比，阻尼係數為μ。設初始時刻小石塊靜止。求其小石塊運動速度與時間的關係。

解：

小石塊遵循的運動方程為

mdv/dt=mg―μv2⑻

這是Riccati方程，它可以精確求解。

依標準變換方式，設

v=（m/μ）（z′/z）⑼

代入⑻式，再作化簡，有

z''―（gμ/m)z=0⑽

⑽式的通解是

z=C1exp（√gμ/m t）+C2exp（－√gμ/m t）⑾

其中，C1和C2是任意常數。

由於小石塊在初始時刻是靜止的，初始條件為

v（0）=0⑿

這等價於

z′（0）=0⒀

因此，容易定出

C2=－C1⒁

將⒁式代入⑾式，再將⑾式代入⑼式，就可得

滿足初始條件的解

v=√mg/μtanh（√μg/m t)⒂

我們可以作一下定性的分析。小石塊初始時刻靜止。因此，隨著時間增加，開始時小石塊速度較小，小石塊所受的阻力影響較小，此時，小石塊與不受阻力的自由落體運動情況相類似，小石塊加速度幾乎是常數。反映在圖1中，起始段t和v的關係是直線。當小石塊速度很大時，重力相對於阻力來說可以忽略，阻力快速增加到很大的數值，導致小石塊的速度幾乎不再增加。此時，小石塊加速度接近零，v幾乎不隨時間而變化。從圖1中可以看到，一段時間后，v相不多是一平行於t軸的直線。

導線電容

真空中兩條圓柱形無窮長平行直導線，橫截面的半徑分別為R1和R2，中心線相距為d(d>R1+R2）。試求它們間單位長度的電容。

解：

設這兩條導線都帶電，單位長度的電荷量分別是為λ和―λ。

我們可以用電像法精確求解。電像法的思路是：

由於在靜電平衡情況時，導線是等勢體，因而我們可設想用偶極線來取代這兩條圓柱形帶電導線，適當地選擇偶極線的位置，使它們所產生的兩個等勢面恰好與原來兩導線的表面重合。這樣就滿足了邊界條件。這裡採用的偶極線是兩條無窮長的均勻帶電平行直線，它們單位長度的電荷量也分別為λ和―λ。這偶極線便是原來兩帶電導線的電像。於是就可以計算電勢，從而求出電容來。為此先求偶極線的等勢面。

以偶極線所在的平面為z-x平面，取笛卡兒坐標系，使偶極線對稱地處在z軸的兩側，它們到z軸的距離都是a。如圖2所示。這偶極線所產生的電勢便為

φ=φ1+φ2

=（λ/2πε0）In（r1′/r1）+（―λ/2πε0）In（r2′/r2）

=（λ/2πε0）In[（r2/r1）（r1′/r2′）]⒃

y

P

r2 r1

R2―λ+λR1 x

O

a a

a2 a1

圖2：帶電導線與其鏡像

式中r1′和r2′分別是偶極線λ和―λ到某個電勢參考點的距離。為方便起見，我們取z軸上的電勢為零，這樣，r1′=r2′=a，於是，⒃式便化為

φ=（λ/2πε0）In（r2/r1）⒄

由於對稱性，平行於z軸的任何一條直線都是偶極線的等勢線。所以，我們只須考慮z-y平面內任意一點P（z，y）的電勢即可。於是

φ=（λ/4πε0）In{[（x2+a2）+y2]/[（x2―a2）+y2]}⒅

故偶極線的等勢面方程便為

[（x2+a2）+y2]/[（x2―a2）+y2]=k2⒆

式中

k2=e4πε0φ/λ⒇

令

c=[（k2+1）/（k2―1）]a（21）

則⒆式可化為

（x―c）2+y2=[4k2/（k2―1）2]a 2（22）

這表明，偶極線的等勢面都是軸線平行於z軸的圓柱面，它們的軸線都在z軸上z=c處，其橫截面的半徑為

R=∣2k/（k2―1）∣a（23）

這個結果啟示，我們可以找到偶極線的兩個等勢面，使它們分別與原來兩導線的表面重合。這隻要下列等式成立就可以了：

a1=∣c1∣=[（k12+1）/（k12―1）]a（24）

R1=∣2k1/（k12―1）∣a（25）

a2=∣c2∣=[（k22+1）/（k22―1）]a（26）

R2=∣2k2/（k22―1）∣a（27）

d=a1+a2（28）

由（24）至（27）式得

a12―R12=a2=a22―R22（29）

原來兩導線表面的方程是

R1：（x―a1）2+y2=R12（30）

R2：（x+a2）2+y2=R22（31）

利用（29）式，可以把（30）和（31）式分別化為

x2+y2+a2=2a1 x（32）

x2+y2+a2=―2a2 x（33）

利用（32）和（33）兩式，由⒅式得出，半徑為R1和R2的兩導線的電勢分別為

φ1=（λ/4πε0）In[（a1+a）/（a1―a）]（34）

φ2=―（λ/4πε0）In[（a2+a）/（a2―a）]（35）

於是兩導線的電勢差便為

U=φ1+φ2=（λ/2πε0）In[（a1+a）（a2―a）/R1R2]（36）

用已知的量消去未知數，可以得出

U=（λ/2πε0）In[（d2―R12―R2）/2R1R2+√[（d2―R12―R2）/2R1R2]2―1]（37）

最後得出原來兩導線為l一段的電容為

C=Q/U=2πε0l/In[（d2―R12―R22）/2R1R2+√[（d2―R12―R22）/2R1R2]2―1]（38）

單位長度的電容為

c=2πε0/In[（d2―R12―R22）/2R1R2+√[（d2―R12―R22）/2R1R2]2―1]（39）

利用反兩曲餘弦關係式

archx=In[（x+√x2―1）]（40）

對本題的精確解表示作簡潔表示

c=2πε0/arch[（d2―R12―R22）/2R1R2]（41）

最後一式可以在一般手冊上查到。

粒子運動

一電荷量為q、靜質量為m0的粒子從原點出發，在一均勻電場E中運動，E=Eez沿z軸方向，粒子的初速度沿y軸方向，試證明此粒子的軌跡為

x=（W0/qE）[cosh（qEy/p0c）―1]（42）

式中p0是粒子出發時動量的值，W0是它出發時的能量。

解：

帶有電荷量q的粒子在電磁場E和B中的相對論性的運動方程為

dp/dt=q（E+v×B）（43）

式中v是粒子的速度，p是粒子的動量

p=mv=mv0/√1－v2/c2（44）

本題運動方程的分量表示式為

dpx=qE

dpy=0

dpz=0（45）

解之，有

px=qEt+C1

py=C2

pz=C3（46）

代入t=0時初始條件

px（0）=0

py（0）=p0

pz（0）=0（47）

定出積分常數后，可知

px=qEt

py=p0

pz=0（48）

粒子的能量為

W=mc2

=√p2c2+m02c4

=√（px2+py2+pz2）c2+m02c4

=√q2E2 c2t2+W02（49）

因dx/dt=qEt/m=qEc2t/√q2E2 c2t2+W02（50）

積分得

x=∫[qEc2t/√q2E2 c2t2+W02]dt

=[√q2E2 c2t2+W02－W02]/qE（51）

又由（48）式得

dy/dt=p0/m=p0c2/√q2E2 c2t2+W02（52）

積分得

y=∫[p0c2/√q2E2 c2t2+W02]dt

=（p0c/qE）arsh（qEct/W0）（53）

或（qEct/W0）=sinh（qEy/p0c）（54）

在（51）式和（54）式中消去t，有

x=（W0/qE）[√1+sinh2（qEy/p0c）－1]（55）

利用恆等變換公式

cosh2x―sinh2x=1（56）

（55）式可以寫成

x=（W0/qE）[cosh2（qEy/p0c）－1]（57）

（57）式是一種懸鏈線。

圖3：勻強電場中粒子的懸鏈線運動軌跡

討論：

因雙曲餘弦泰勒級數展開式是

cosh（x）=1+x2/2!+x4/4!+x6/6!+……（58）

當v/c→0時，保留前2項，得

x=（qE/2m v02）y2（59）

（59）式是拋物線軌跡。《普通物理學》教材用經典牛頓力學求解，普遍會給有這個結果。這表示，非相對論確是相對論在v/c→0時的極限。或者說，（59）式成立的條件是v/c<<1，這也是牛頓力學的適用範圍。

如著名的KdV（Korteweg-de Vries）方程的形式為

ux+uux+βuxxx=0（60）[2]

它是非線性的頻散方程，其中β是頻散係數。用雙曲函數展開法求其某些特殊精確解。

解：

考慮其行波解

u（x，t）=φ（ξ）（61）

其中，

ξ=kx－ωt+ξ0（62）

KdV方程成為

－ωφξ+kφφξ+k3βφξξξ=0（63）

記

f=1/（coshξ+r），g=sinhξ/（coshξ+r）（64）

嘗試

φ=a0+a1f+a2g（65）

注意存在關係式

df/dξ=－fg

dg/dξ=1－g2－rg

g2=1－2rf+（r2－1）f2（66）

將（65）式代入（63）式，並在（66）式的幫助下使所得方程中各項只含有f和g的冪次項，且g的冪次項不大於1。合併f和g的同次冪項並取其係數為零，就得到方程（63）對應的非線性代數方程組

－6βk3b1（r2－1）2=0,

－6βk3a1（r2－1）=0,

－2kb1（r2－1）（－6βk2r+a1）=0,

－k（－6βk2r a1+a12－b12+b12r2）=0,

b1（4βk3+ka0－ka0r2+3ka1 r－7βk3 r2+cr2－c）=0,

ωa1+kb12 r－βk3 a1－ka0a1=0,

－b1（ka1+ωr－βk3r－ka0r）=0（67）

用計算機代數系統Maple對此超定方程組進行運算，可求得k≠0，ω≠0時的一個非平凡精確解

φ=（ω－βk3）/k+6βk2/（coshξ+1）=0（68）

其中，k、ω、ξ0為任意常數。

（68）式是孤波解，圖4繪出了其函數圖像形狀（作圖時取了β=1/6 k2，ω=βk3）。

圖4：KdV方程的孤波解

從以上的討論中可知，無論是在經典或近代的物理學內容中，還是在正在發展中的物理學內容中，雙曲函數起著不可或缺的重要作用。

懸鏈線

形如y=a cosh(x/a)(a為常數）的函數的圖象又叫懸鏈線，可以由柔軟的繩子得到，有點象拋物線，但其實兩者差距很大。據說萊布尼茲（Leibniz）於1690年最先解出懸鏈線方程，惠更斯（Huygens）和伯努利兄弟（Jacob Bernoulli,Johann Bernoulli）隨其後。惠更斯在1691年把懸鏈線命名為catenary.懸鏈線與拋物線有這樣的關係：懸鏈線是直線上滾動的拋物線的焦點的運動軌跡。懸鏈線的頂點的漸開線是曳物線（tractrix).這條曳物線的漸進線稱為懸鏈線的準線，懸鏈線繞準線旋轉形成的曲面叫做懸鏈面.

設最低點A處受水平向左的拉力H，右懸掛點處表示為C點，在AC弧線區段任意取一段設為B點，則B受一個斜向上的拉力T，設T和水平方向夾角為θ，繩子的質量為m，受力分析有：Tsinθ=mg；Tcosθ=H，tanθ=dy/dx=mg/H，mg=ρs，，其中s是右段AB繩子的長度，ρ是繩子線重量密度，代入得微分方程dy/dx=ρs/H；利用弧長公式ds=√（1+dy^2/dx^2）*dx；所以s=∫√（1+dy^2/dx^2）*dx;所以把s帶入微分方程得dy/dx=ρ∫√（1+dy^2/dx^2）*dx/H;.....⑴對於⑴設p=dy/dx微分處理得p'=ρ/H*√（1+p^2）......⑵p'=dp/dx;對⑵分離常量求積分∫dp/√（1+p^2）=∫ρ/H*dx得ln[p+√（1+p^2）]=ρx/H+C，即asinhp（反雙曲正弦）=ρx/H+C當x=0時，dy/dx=p=0；帶入得C=0；整理得asinhp=ρx/H另祥解：（ln[p+√（1+p^2）]=ρx/H）；p=sh（ρx/H)（1+p^2=e^（2ρx/H)-2pe^（ρx/H)+p^2）；（p=[e^（ρx/H)-e^(-ρx/H)]/2=dy/dx）；y=ch（ρx/H)*H/ρ（y=H/（2ρ）*[e^（ρx/H)+e^(-ρx/H)]）；令a=H/ρ：y=a*cosh(x/a)（y=a[e^(x/a)+e^(-x/a)]/⑵=a*cosh(x/a））。