雙軸晶體具有兩個光軸的晶體,其折射率橢球為三軸橢球體。屬於三斜晶系、單斜晶系和正交晶系的晶體都是光學雙軸晶體。
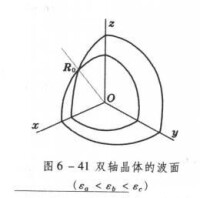
雙軸晶體的波面
根據電磁理論可以算出,雙軸晶體的波面(射線面)具有如圖所示的複雜形式。它在三個坐標面上的剖面都由一個圓和一個橢圓組成。在這些圖中x、y 、z軸是按ε、ε、ε增大的順序選取的,在zx平面的每個
象限內兩層波面相交於一點R,
波面在此處形成一個“酒窩”。當光線沿OR方向傳播時,各光束的射線速度相同。OR方向叫做晶體的射線軸。為了在
射線面的圖中尋找光軸的方向,只需在zx剖面圖中作圓和橢圓的公切線,令它與圓的切點為N,ON方向稱為晶體的光軸,因為當波法線 k沿此方向時,各光束的相速相同。可以看出,在z軸兩側各有一條光軸和射線軸,故
晶體具有兩條光軸和兩條射線軸。
光在晶體中傳播時,在不平行於光軸方向上,由於
e光和o光傳播速度不同,而出現兩個不同折射率的光的像,這種現象叫做
雙折射現象。雙折射現象有兩類,單軸晶體和雙軸晶體。
雙軸晶體的三個主介電係數都不相等,即ε≠ε≠ε,因而n≠n≠n。通常主介電係數按ε< ε<ε取值。這類晶體之所以叫雙軸晶體,是因為它有兩個光軸,當光沿該二光軸方向傳播時,其相應的二特許線偏振
光波的傳播速度(或折射率)相等。由波法線菲涅耳方程式可以證明,雙軸晶體的兩個光軸都在xOx平面內,並且與x軸的夾角分別為β和-β。對於β小於45°的晶體,叫正雙軸晶體,β大於45°的晶體,叫負雙軸晶體。由這兩個光軸構成的平面叫
光軸面。
由
電磁場理論已知,
介電常數ε是表徵
介質電學特性的參量。由
固體物理學知道,不同晶體的結構具有不同的空間
對稱性,自然界中存在的晶體按其空間對稱性的不同,分為七大
晶系:
立方晶系;
四方晶系;六方晶系;三方晶系;正方晶系;單斜晶系;三斜晶系。由於它們的對稱性不同,所以在主軸坐標系中介電張量的獨立分量數目不同,各晶系的介電張量矩陣形式如表所示。由該表可見,
三斜、單斜和正交晶系中,主介電係數ε≠ε≠ε,這幾類晶體在光學上稱為雙軸晶體;三方、四方、六方晶系中,主介電係數ε=ε≠ε,這幾類晶體在光學上稱為單軸品體;立方晶系在光學上是各向同性的,ε=ε=ε。
1832年,
英國科學家
哈密頓預言,當波矢 K與雙軸晶體一個光軸重合時,傳播的光能將分佈在空心錐面上,出射光即為錐面光束,則在橫截平面上觀察可見到一個光環。這種現象後來被人所證實,但是170多年來這種現象只是作為光波動說的一種典型例證,而在實踐上卻沒有獲得應用。20世紀末期,我國的一些科技工作者對錐折射現象進行了深入研究,不僅獲得了大張角的激光錐面光束,而且實現了錐光控制,可以進行激光圓錐掃描,為錐折射現象的應用奠定了技術基礎。
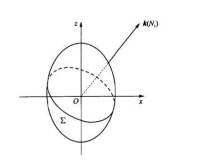
光波沿雙軸晶體的一個光軸傳播
下面詳細研究為什麼會產生錐折射現象以及怎樣產生錐折射。如圖所示為雙軸晶體的 折射率橢球,設單位光波矢k與雙軸晶體一個光軸N重合,過折射率橢球中心O做波矢 k的垂面,則與折射率橢球的交線是一個圓;設此圓為∑,因差電位移矢量 D與波矢 k垂直,所以必然在∑平面上。當∑是橢圓截痕時,其長、短軸方向為允許的電位移D,所以一般有兩個電位移與同一
波矢 k相對應;而現在的情況即∑是一葉圓,長、短軸無法確定,所以有無數個 D矢量與同一波矢 k相對應,無數個 D矢量對應無數個 E矢量,從而決定光線S是無數的,可以證明這無數條S光線分佈在一個錐面上。
見下圖,平面A上的O點為光波入射點,在晶體內的光波矢 k與光軸N重合;平面π為 k的垂面,直線AB為平面Λ和平面π的交線,Q點為 k在平面π上的垂足,根據光波在非均勻介質中的普遍傳播規律 D⊥ k,所以有
kD+ kD+ kD= 0
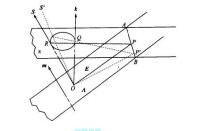
雙軸晶體的錐折射光線傳播圖
而雙軸晶體的光軸取主軸
坐標系時在Oxz平面上,所以 k也在Oxz平面上,即是k為零。利用電位移與電場矢量的關係式D=εE,D=εE,於是得到
kεE+ kεE= 0
令矢量m=kεa+ kεc,式中,a、c為x、z方向的單位矢量,則有
mE+ mE = 0
上面的錐折射是在晶體內部,稱為內錐形折射。如果用平行晶體薄片做實驗,
晶片表面與一個光軸垂直,從薄片的出射光經出射面再次產生折射,便形成圓筒光束。若晶片的入射面採用會聚光入射,在晶片出射面可產生圓錐面光束,稱為外錐折射。早期用天然雙軸晶體做錐形折射實驗,得到的
錐角較小,目前用人工雙軸晶體,比如KNbO,可以得到20°以上的全錐角;通過晶體的電光效應或幾何光學方法可以實現錐角的控制,製成
圓錐掃描器。雙軸晶體的錐折射應用雖然目前還未被人們所重視,但是隨著人造優質雙軸晶體的發展和激光技術的講瘩,錐折射現象有可能在制導和隱身測距方面得到應用。



