黎曼函數
一個特殊函數
黎曼函數(Riemann function)是一個特殊函數,由德國數學家黎曼發現提出,黎曼函數定義在[0,1]上,其基本定義是:R(x)=1/q,當x=p/q(p,q都屬於正整數,p/q為既約真分數);R(x)=0,當x=0,1和(0,1)內的無理數。
徠黎曼函數在高等數學中被廣泛應用,在很多情況下可以作為反例來驗證某些函數方面的待證命題。
函數可積性的勒貝格判據指出,一個有界函數是黎曼可積的,當且僅當它的所有不連續點組成的集合測度為0。黎曼函數的不連續點集合即為有理數集,是可數的,故其測度為0,所以由勒貝格判據,它是黎曼可積的。
定義在區間上的函數:
當 (都屬於正整數,為既約真分數)時,;
當 和無理數時,
稱為黎曼函數
從黎曼函數的定義可知,它具有如下一些特徵:
(1)黎曼函數是區間上的有界函數,其上確界是,下確界是 0 ,其值域只有一個,聚點是0,它也是數列的極限值,其中為自然數
(2)黎曼函數在有理點的圖象關於直線對稱
(3)對於,使得 的區間 中的有理數只有有限多個
定理:黎曼函數在區間內的極限處處為0。
證明:對任意,任給正數,考慮除 以外所有黎曼函數的函數值大於等於的點,因為黎曼函數的正數值都是的形式(),且對每個,函數值等於的點都是有限的,所以除以外所有函數值大於等於的點也是有限的。設這些點,連同0、1,與 的最小距離為,則 的半徑為的去心鄰域中所有點函數值均在中,從而黎曼函數在時的極限為0。
推論:黎曼函數在內的無理點處處連續,有理點處處不連續。
推論:黎曼函數在區間上是黎曼可積的(實際上,黎曼函數在上的積分為0)
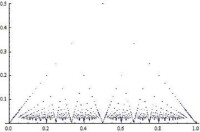
黎曼函數
從黎曼函數的圖像中可以看出,函數值比較大的點是很稀疏的,隨著函數值的減小,點在橫向和縱向上都變得越來越密集。
根據圖像的特點,黎曼函數有時也被稱為爆米花函數、雨滴函數。
如果x為任意無理數,;
如果() ,即為任意非零有理數,;
如果,。
這樣定義的黎曼函數上的所有無理點處處連續,有理點處處不連續。

黎曼函數
1847年,黎曼轉到柏林大學學習,成為雅可比、狄利克萊、施泰納、艾森斯坦的學生。1849年重回哥廷根大學攻讀博士學位,成為高斯晚年的學生。
1851年,黎曼獲得數學博士學位;1854年被聘為哥廷根大學的編外講師;1857年晉陞為副教授;1859年接替去世的狄利克雷被聘為教授。
因長年的貧困和勞累,黎曼在1862年婚後不到一個月就開始患胸膜炎和肺結核,其後四年的大部分時間在義大利治病療養。1866年7月20日病逝於義大利,終年39歲。
黎曼是世界數學史上最具獨創精神的數學家之一。黎曼的著作不多,但卻異常深刻,極富於對概念的創造與想象。黎曼在其短暫的一生中為數學的眾多領域作了許多奠基性、創造性的工作,為世界數學建立了豐功偉績。
19世紀數學最獨特的創造是複變函數理論的創立,它是18世紀人們對複數及複函數理論研究的延續。1850年以前,柯西、雅可比、高斯、阿貝爾、維爾斯特拉斯已對單值解析函數的理論進行了系統的研究,而對於多值函數僅有柯西和皮瑟有些孤立的結論。
1851年,黎曼在高斯的指導下完成題為《單複變函數的一般理論的基礎》的博士論文,後來又在《數學雜誌》上發表了四篇重要文章,對其博士論文中思想的做了進一步的闡述,一方面總結前人關於單值解析函數的成果,並用新的工具予以處理,同時創立多值解析函數的理論基礎,並由此為幾個不同方向的進展鋪平了道路。
柯西、黎曼和維爾斯特拉斯是公認的複變函數論的主要奠基人,而且後來證明在處理複函數理論的方法上黎曼的方法是本質的,柯西和黎曼的思想被融合起來,維爾斯特拉斯的思想可以從柯西—黎曼的觀點推導出來。
在黎曼對多值函數的處理中,最關鍵的是他引入了被後人稱“黎曼面”的概念。通過黎曼面給多值函數以幾何直觀,且在黎曼面上表示的多值函數是單值的。他在黎曼面上引入支點、橫剖線、定義連通性,開展對函數性質的研究獲得一系列成果。
經黎曼處理的複函數,單值函數是多值函數的待例,他把單值函數的一些已知結論推廣到多值函數中,尤其他按連通性對函數分類的方法,極大地推動了拓撲學的初期發展。他研究了阿貝爾函數和阿貝爾積分及阿貝爾積分的反演,得到著名的黎曼—羅赫定理,首創的雙有理變換構成19世紀後期發展起來的代數幾何的主要內容。
黎曼為完善其博士論文,在結束時給出其函數論在保形映射的幾個應用,將高斯在1825年關於平面到平面的保形映射的結論推廣到任意黎曼面上,並在文字的結尾給出著名的黎曼映射定理。
黎曼對數學最重要的貢獻還在於幾何方面,他開創的高維抽象幾何的研究,處理幾何問題的方法和手段是幾何史上一場深刻的革命,他建立了一種全新的後來以其名字命名的幾何體系,對現代幾何乃至數學和科學各分支的發展都產生了巨大的影響。
1854年,黎曼為了取得哥廷根大學編外講師的資格,對全體教員作了一次演講,該演講在其逝世后的兩年(1868年)以《關於作為幾何學基礎的假設》為題出版。演講中,他對所有已知的幾何,包括剛剛誕生的非歐幾何之一的雙曲幾何作了縱貫古今的概要,並提出一種新的幾何體系,後人稱為黎曼幾何。
為競爭巴黎科學院的獎金,黎曼在1861年寫了一篇關於熱傳導的徠文章,這篇文章後來被稱為他的“巴黎之作”。文中對他1854年的文章作了技術性的加工,進一步闡明其幾何思想。該文在他死後收集在1876年他的《文集》中。
黎曼主要研究幾何空間的局部性質,他採用的是微分幾何的途徑,這同在歐幾里得幾何中或者在高斯、波爾約和羅巴切夫斯基的非歐幾何中把空間作為一個整體進行考慮是對立的。黎曼擺脫高斯等前人把幾何對象局限在三維歐幾里得空間的曲線和曲面的束縛,從維度出發,建立了更一般的抽象幾何空間。
黎曼引入流形和微分流形的概念,把維空間稱為一個流形,維流形中的一個點可以用個可變參數的一組特定值來表示,而所有這些點的全體構成流形本身,這個可變參數稱為流形的坐標,而且是可微分的,當坐標連續變化時,對應的點就遍歷這個流形。
黎曼仿照傳統的微分幾何定義流形上兩點之間的距離、流形上的曲線、曲線之間的夾角。並以這些概念為基礎,展開對維流形幾何性質的研究。在維流形上他也定義類似於高斯在研究一般曲面時刻劃曲面彎曲程度的曲率。他證明他在維流形上維數等於三時,歐幾里得空間的情形與高斯等人得到的結果是一致的,因而黎曼幾何是傳統微分幾何的推廣。
黎曼發展了高斯關於一張曲面本身就是一個空間的幾何思想,開展對維流形內蘊性質的研究。黎曼的研究導致另一種非歐幾何——橢圓幾何學的誕生。
在黎曼看來,有三種不同的幾何學。它們的差別在於通過給定一點做關於定直線所作平行線的條數。如果只能作一條平行線,即為熟知的歐幾里得幾何學;如果一條都不能作,則為橢圓幾何學;如果存在一組平行線,就得到第三種幾何學,即羅巴切夫斯基幾何學。黎曼因此繼羅巴切夫斯基以後發展了空間的理論,使得一千多年來關於歐幾里得平行公理的討論宣告結束。他斷言,客觀空間是一種特殊的流形,預見具有某種特定性質的流形的存在性。這些逐漸被後人一一予以證實。
由於黎曼考慮的對象是任意維數的幾何空間,對複雜的客觀空間有更深層的實用價值。所以在高維幾何中,由於多變數微分的複雜性,黎曼採取了一些異於前人的手段使表述更簡潔,並最終導致張量、外微分及聯絡等現代幾何工具的誕生。愛因斯坦就是成功地以黎曼幾何為工具,才將廣義相對論幾何化。現在,黎曼幾何已成為現代理論物理必備的數學基礎。
黎曼除對幾何和複變函數方面的開拓性工作以外,還以其對19世紀初興起的完善微積分理論的傑出貢獻載入史冊。
18世紀末到19世紀初,數學界開始關心數學最龐大的分支——微積分在概念和證明中表現出的不嚴密性。波爾查諾、柯西、阿貝爾、狄利克萊進而到維爾斯特拉斯,都以全力的投入到分析的嚴密化工作中。黎曼由於在柏林大學從師狄利克萊研究數學,且對柯西和阿貝爾的工作有深入的了解,因而對微積分理論有其獨到的見解。
1854年黎曼為取得哥廷根大學編外講師的資格,需要他遞交一篇反映他學術水平的論文。他交出的是《關於利用三角級數表示一個函數的可能性的》文章。這是一篇內容豐富、思想深刻的傑作,對完善分析理論產生深遠的影響。
柯西曾證明連續函數必定是可積的,黎曼指出可積函數不一定是連續的。關於連續與可微性的關係上,柯西和他那個時代的幾乎所有的數學家都相信,而且在後來50年中許多教科書都“證明”連續函數一定是可微的。黎曼給出了一個連續而不可微的著名反例,最終講清連續與可微的關係。
黎曼建立了如現在微積分教科書所講的黎曼積分的概念,給出了這種積分存在的必要充分條件。
黎曼用自己獨特的方法研究傅立葉級數,推廣了保證博里葉展開式成立的狄利克萊條件,即關於三角級數收斂的黎曼條件,得出關於三角級數收斂、可積的一系列定理。他還證明:可以把任一條件收斂的級數的項適當重排,使新級數收斂於任何指定的和或者發散。
19世紀數論中的一個重要發展是由狄利克萊開創的解析方法和解析成果的導入,而黎曼開創了用複數解析函數研究數論問題的先例,取得跨世紀的成果。
1859年,黎曼發表了《在給定大小之下的素數個數》的論文。這是一篇不到十頁的內容極其深到的論文,他將素數的分佈的問題歸結為函數的問題,現在稱為黎曼函數。黎曼證明了函數的一些重要性質,並簡要地斷言了其它的性質而未予證明。
在黎曼死後的一百多年中,世界上許多最優秀的數學家盡了最大的努力想證明他的這些斷言,並在作出這些努力的過程中為分析創立了新的內容豐富的新分支。如今,除了他的一個斷言外,其餘都按黎曼所期望的那樣得到了解決。
那個未解決的問題現稱為“黎曼猜想”,即:在帶形區域中的一切零點都位於去這條線上(希爾伯特23個問題中的第8個問題),這個問題迄今沒有人證明。對於某些其它的域,布爾巴基學派的成員已證明相應的黎曼猜想。數論中很多問題的解決有賴於這個猜想的解決。黎曼的這一工作既是對解析數論理論的貢獻,也極大地豐富了複變函數論的內容。
在黎曼博士論文發表以前,已有一些組合拓撲的零散結果,其中著名的如歐拉關於閉凸多面體的頂點、棱、面數關係的歐拉定理。還有一些看起來簡單又長期得不到解決的問題:如哥尼斯堡七橋問題、四色問題,這些促使了人們對組合拓撲學(當時被人們稱為位置幾何學或位置分析學)的研究。但拓撲研究的最大推動力來自黎曼的複變函數論的工作。
黎曼在1851年他的博士論文中,以及在他的阿貝爾函數的研究里都強調說,要研究函數,就不可避免地需要位置分析學的一些定理。按現代拓撲學術語來說,黎曼事實上已經對閉曲面按虧格分類。值得提到的是,在其學位論文中,他說到某些函數的全體組成(空間點的)連通閉區域的思想是最早的泛函思想。
比薩大學的數學教授貝蒂曾在義大利與黎曼相會,黎曼由於當時病魔纏身,自身已無能力繼續發展其思想,把方法傳授給了貝蒂。貝蒂把黎曼面的拓撲分類推廣到高維圖形的連通性,並在拓撲學的其他領域作出傑出的貢獻。黎曼是當之無愧的組合拓撲的先期開拓者。
19世紀後半葉,人們對黎曼研究阿貝爾積分和阿貝爾函數所創造的雙有理變換的方法產生極大的興趣。當時他們把代數不變數和雙有理變換的研究稱為代數幾何。
黎曼在1857年的論文中認為,所有能彼此雙有理變換的方程(或曲面)屬於同一類,它們有相同的虧格。黎曼把常量的個數叫做“類模數”,常量在雙有理變換下是不變數。“類模數”的概念是現在“參模”的特殊情況,研究參模上的結構是現代最熱門的領域之一。
著名的代數幾何學家克萊布希後來到哥廷根大學擔任數學教授,他進一步熟悉了黎曼的工作,並對黎曼的工作給予新的發展。雖然黎曼英年早逝,但世人公認,研究曲線的雙有理變換的第一個大的步驟是由黎曼的工作引起的。
在數學物理、微分方程等其他領域的豐碩成果
黎曼不但對純數學作出了劃時代的貢獻,他也十分關心物理及數學與物理世界的關係,他寫了一些關於熱、光、磁、氣體理論、流體力學及聲學方面的有關論文。他是對衝擊波作數學處理的第一個人,他試圖將引力與光統一起來,並研究人耳的數學結構。他將物理問題抽象出的常微分方程、偏微分方程進行定論研究得到一系列豐碩成果。
黎曼在1857年的論文《對可用高斯級數表示的函數的理論的補充》,及同年寫的一個沒有發表而後收集在其全集中的一個片斷中,他處理了超幾何微分方程和討論帶代數係數的階線性微分方程。這是關於微分方程奇點理論的重要文獻。
19世紀後半期,許多數學家花了很多精力研究黎曼問題,然而都失敗了,直到1905年希爾伯特和Kellogg藉助當時已經發展了的積分方程理論,才第一次給出完全解。
黎曼在常微分方程理論中自守函數的研究上也有建樹,在他的1858~1859年關於超幾何級數的講義和1867年發表的關於極小正曲面的一篇遺著中,他建立了為研究二階線性微分方程而引進的自守函數理論,即現在通稱的黎曼——許瓦茲定理。
在偏微分方程的理論和應用上,黎曼在1858年~1859年論文中,創造性的提出解波動方程初值問題的新方法,簡化了許多物理問題的難度;他還推廣了格林定理;對關於微分方程解的存在性的狄里克萊原理作了傑出的工作。
黎曼在物理學中使用的偏微分方程的講義,後來由韋伯以《數學物理的微分方程》編輯出版,這是一本歷史名著。
不過,黎曼的創造性工作當時未能得到數學界的一致公認,一方面由於他的思想過於深邃,當時人們難以理解,如無自由移動概念非常曲率的黎曼空間就很難為人接受,直到廣義相對論出現才平息了指責;另一方面也由於他的部分工作不夠嚴謹,如在論證黎曼映射定理和黎曼—羅赫定理時,濫用了狄利克雷原理,曾經引起了很大的爭議。
黎曼的工作直接影響了19世紀後半期的數學發展,許多傑出的數學家重新論證黎曼斷言過的定理,在黎曼思想的影響下數學許多分支取得了輝煌成就。
