色線

流線的定義

流線（stream line）是表示某一瞬時流體各點流動趨勢的曲線，曲線上任一點的切線方向與該點的流速方向重合。圖3-1為流線譜中顯示的流線形狀。

流線的作法：

在流場中任取一點，

繪出某時刻通過該點的流體質點的流速矢量u1，再畫出距1點很近的2點在同一時刻通過該處的流體質點的流速矢量u2…，如此繼續下去，得一折線1234 …，若各點無限接近，其極限就是某時刻的流線。

流線是歐拉法分析流動的重要概念。

流線的性質

a.同一時刻的不同流線，不能相交。

因為根據流線定義，在交點的液體質點的流速向量應同時與這兩條流線相切，即一個質點不可能同時有兩個速度向量。

b.流線不能是折線，而是一條光滑的曲線。

因為流體是連續介質，各運動要素是空間的連續函數。

c.流線簇的疏密反映了速度的大小（流線密集的地方流速大，稀疏的地方流速小）。

因為對不可壓縮流體，元流的流速與其過水斷面面積成反比。

色線

又稱脈線，是源於一點的很多流體質點在同一瞬時的連線。

例如：為顯示流動在同一點投放示蹤染色體的線，以及香煙線都是色線。

1.層流與紊流

亦稱片流，是指流體質點不互相混雜，流體質點作有條不紊的有序的直線運動。

特點：

（1）有序性。

（2）水頭損失與流速的一次方成正比。

（3）在流速較小且雷諾數Re較小時發生。

層流遵循牛頓內摩擦定律，粘性抑制或約束質點作橫向運動。

亦稱湍流，是指隨流速增大，流層逐漸不穩定，質點相互混摻，流體質點沿很不規則的路徑運動。

特點：

（1）無序性、隨機性、有旋性、混合性。

（2）水頭損失與流速的1.75~2次方成正比。

（3）在流速較大且雷諾數較大時發生。

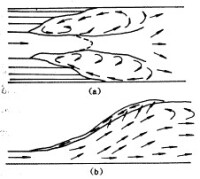
紊流是工程實踐中最常見的一種流動，如圖3-9，紊流微團不僅有橫向脈動，而且有相對於流體總運動的反向運動，紊流中質點運動要素具有隨機性，流速的大小方向隨機變化，沒有兩個流體質點可以沿著同樣的、甚至相似的路徑運動。紊流就是壓力表指針不斷擺動的原因。

2.恆定流與非恆定流

恆定流（steady flow）：又稱定常流，是指流場中的流體流動，空間點上各水力運動要素均不隨時間而變化。

嚴格的恆定流只可能發生在層流，在紊流中，由於流動的無序，其流速或壓強總有脈動，但若取時間平均流速（時均流速），若其不隨時間變化，則認為該紊流為恆定流。

非恆定流

在非恆定流情況下，流線的位置隨時間而變；流線與跡線不重合。

在恆定流情況下，流線的位置不隨時間而變，且與跡線重合。

3.均勻流與非均勻流

均勻流——流線是平行直線的流動

均勻流中各過水斷面上的流速分布圖沿程不變，過水斷面是平面，沿程各過水斷面的形狀和大小都保持一樣。例：等直徑直管中的液流或者斷面形狀和水深不變的長直渠道中的水流都是均勻流。

非均勻流——流線不是平行直線的流動

非均勻流中流場中相應點的流速大小或方向或同時二者沿程改變，即沿流程方向速度分佈不均。例：流體在收縮管、擴散管或彎管中的流動。（非均勻流又可分為急變流和漸變流）

4.漸變流與急變流

非均勻流中如流動變化緩慢，流線的曲率很小接近平行，過流斷面上的壓力基本上是靜壓分佈者為漸變流(gradually varied flow)，否則為急變流。

漸變流——沿程逐漸改變的流動。

特徵：流線之間的夾角很小即流線幾乎是平行的，同時流線的曲率半徑又很大（即流線幾乎是直線），其極限是均勻流，過水斷面可看作是平面。漸變流的加速度很小，慣性力也很小，可以忽略不計。

急變流——沿程急劇改變的流動。

特徵：流線間夾角很大或曲率半徑較小或二者兼而有之，流線是曲線，過水斷面不是一個平面。急變流的加速度較大，因而慣性力不可忽略。

一元流(one-dimensional flow):流體在一個方向流動最為顯著，其餘兩個方向的流動可忽略不計，即流動流體的運動要素是一個空間坐標的函數。若考慮流道（管道或渠道）中實際液體運動要素的斷面平均值，則運動要素只是曲線坐標s的函數，這種流動屬於一元流動。

二元流(two-dimensional flow):流體主要表現在兩個方向的流動，而第三個方向的流動可忽略不計，即流動流體的運動要素是二個空間坐標（不限於直角坐標）函數。

三元流

三元流（three-dimensional flow):流動流體的運動要素是三個空間坐標函數。例如水在斷面形狀與大小沿程變化的天然河道中流動，水對船的繞流等等，這種流動屬於三元流動。

拉格朗日方法（lagrangian method）是以流場中每一流體質點作為描述對象的方法，它以流體個別質點隨時間的運動為基礎，通過綜合足夠多的質點（即質點系）運動求得整個流動。——質點系法

（a,b,c）為t=t0起始時刻質點所在的空間位置坐標，稱為拉格朗日數。所以，任何質點在空間的位置（x,y,z）都可看作是（a,b,c）和時間t的函數

（1）（a,b,c）=const , t為變數，可以得出某個指定質點在任意時刻所處的位置。

（2）（a,b,c）為變數,t=const，可以得出某一瞬間不同質點在空間的分佈情況。

由於流體質點的運動軌跡非常複雜，而實用上也無須知道個別質點的運動情況，所以除了少數情況（如波浪運動）外，在工程流體力學中很少採用。

歐拉法（euler method）是以流體質點流經流場中各空間點的運動即以流場作為描述對象研究流動的方法。——流場法。

它不直接追究質點的運動過程，而是以充滿運動液體質點的空間——流場為對象。研究各時刻質點在流場中的變化規律。將個別流體質點運動過程置之不理，而固守於流場各空間點。通過觀察在流動空間中的每一個空間點上運動要素隨時間的變化，把足夠多的空間點綜合起來而得出的整個流體的運動情況。

（1）時變加速度（當地加速度）（local acceleration）——流動過程中流體由於速度隨時間變化而引起的加速度；

（2）位變加速度（遷移加速度）（connective acceleration）——流動過程中流體由於速度隨位置變化而引起的加速度。