積分學
研究積分性質的學科
目錄
積分學的最基本的概念是關於一元函數的定積分與不定積分。蘊含在定積分概念中的基本思想是通過有限逼近無限。因此極限方法就成為建立積分學嚴格理論的基本方法。定積分定義比較完整地概括了積分思想，也比較深刻地揭示了概念的實質。然而這樣定義的積分，除非是在某些極為特殊的情況下，很難直接地用於實際的計算。通常的辦法是先計算被積函數的不定積分，再利用牛頓-萊布尼茨公式算出它的定積分值。不過，即使是對於初等函數，計算不定積分的問題也不能完全地得到解決，因為初等函數的不定積分未必仍然是初等函數。所以不得不考慮進行積分的近似計算並且相應地引進一些非初等函數的新函數。所有這一切使得積分的計算成為很突出的問題。
定積分 促成定積分概念形成的一個問題是幾何方面的計算平面上的曲邊形面積。這個問題相當古老。儘管面積概念自古就已被直觀地、經驗地理解著，卻缺乏一般可行的計算方法。如阿基米德等古希臘數學家，用所謂“窮竭法”算出了圓、弓形與拋物線弓形的面積。中國古代數學家劉徽創造了所謂“割圓術”，他從圓內接正六邊形起算，令邊數成倍地增加，再逐個算出正六邊形，正十二邊形，正二十四邊形……的面積，然後用這一串面積序列來逼近圓面積。不過，古代關於計算面積的樸素思想遠未達到形成面積概念的境界。他們只完成了一些特殊的曲邊形面積的計算。直到17世紀，I.牛頓、G.W.萊布尼茨才明確地提出了面積計算的普遍方法。
曲邊梯形的面積 是指區間上的非負連續函數ƒ(x)與x軸及直線圍成的一塊面積。由於曲線形總是用有限個這種圖形組成的，因而計算它的面積是一個基本問題。首先可以把曲邊梯形的面積S 劃分成一些小曲邊梯形的面積 ΔSi之和（圖1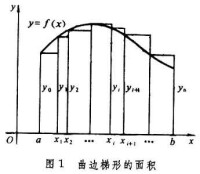
）：，再用小矩形的面積來代替每一塊小面積ΔS表示各個小矩形面積之和，它與的劃分來實現的，如果令λ為最大的區間長度，即那麼曲邊梯形面積就有極限表示：
積分學
促使定積分概念產生的另一類問題是物理學方面的求變化過程中的積累量。例如，變速運動在一段時間內行進的路程，變力使物體運動一段路程所作的功等等。計算的方法仍然是將所求的量（路程l或功W）劃分為“無窮小量”之和，並用均勻變化過程的計算方法來近似計算 ΔЛi或Δwi。如果ΔЛi是時間間隔中物體運動的路程，則可用在此時間間隔內的勻速運動所行進的路程
來近似地代替ΔЛi，其中 可以是物體在ti-1到ti之間任何時刻的速度。如果Δwi是變力F(s)在小段路程間隔上所作的功，則可用在此小段路程上常力作功來近似代替Δwi,其中可以是物體在路程si-1 到si之間任何一點處所受的力。這時和式
與所求的量l、W 的差別，將隨“無窮小量”劃分的細密程度的增高而愈來愈小。由於所謂“無窮小量” ΔЛi或Δwi是通過對區間的劃分來實現的，若令λ為最大的小區間長度，那麼所求的量是
無論計算曲邊梯形面積還是變速運動的路程或變力所作的功，都是對一個函數在一個確定的區間上，求出其內在的一個確定的數值(S,l或W)，而且方法是共同的：都是在對區間進行分划的基礎上構造出一個特殊形式的和，然後求出其極限值。對一個抽象的定義在某個區間上的函數ƒ(x)，也可用同樣的方法尋求它內在的某個確定的數值，而被稱之為函數ƒ(x)在區間上的定積分。下面敘述的是誕生於19世紀的嚴格的定積分概念，它基於A.-L.柯西對連續函數的積分的研究以及（G.F.）B.黎曼關於某種不連續函數的積分的研究。
定積分的定義 設函數ƒ(x)定義在區間上，在這區間上順序插入任意若干分點：
從而把區間分劃為n個子區間，在每個子區間上任取一點ξi並作和式
令λ表示分划的最大的子區間的長度。如果當λ→0時，和式σ趨於某一個確定的極限I,則稱這極限I為函數ƒ(x)在區間上的定積分或黎曼積分，記為
這時又說函數ƒ(x)在區間上是黎曼可積的。
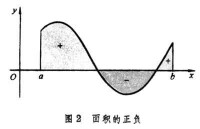
當上的連續函數時，積分有著明顯的幾何意義，它表示由曲線所圍成的曲邊梯形的面積（圖1）。至於一般的函數，如果規定x軸下面的曲邊形的面積是負的，則積分給出了如圖2中幾部分“有向”面積的代數和。
積分學
而對於被積函數是線性的，即
式中α，β為常數；並且當 時，成立
此外，還有分別關於被積函數與積分區間的中值定理：
第一中值定理 對於區間上一個連續函數ƒ(x)與一個不變號的可積函數φ(x)，一定存在該區間上一點ξ，使得
第二中值定理 對於區間上一個單調函數ƒ(x)與一個可積函數g(x),一定存在該區間上一點ξ,使得
黎曼可積函數類 根據定積分的定義可以判斷，凡無界函數都不是黎曼可積的。全體黎曼可積的有界函數組成的函數類稱為黎曼可積函數類。區間上的有界函數ƒ(x)黎曼可積的充分必要條件是
式中 分別是區間上ƒ(x)的上、下確界。這個充分必要條件刻畫了黎曼可積函數類僅由那些不連續的範圍不甚廣的有界函數所組成。以上結論又可以確切地敘述為：黎曼積分存在的一個充分必要條件是被積函數在積分區間上有界，並且其不連續點能夠被一些區間所覆蓋，而這些區間的總長度可以任意小。
定積分概念可以推廣到廣義積分、含參變數積分、多元函數在相應的高維區域上的積分(見多元微積分學)等。近代尤其重要的推廣是對黎曼積分的定義加以改造而構成勒貝格積分的概念。勒貝格以他關於點集的測度概念為基礎，建立的這一新的積分理論擴充了黎曼可積函數類，克服了黎曼積分在極限運算方面存在的局限性，使有關極限與積分交換次序的理論變得非常簡明（見勒貝格積分）。
不定積分 某些實際問題的解決常常歸結到尋求一個函數，使它以某一個已知函數為導數。例如，研究一個質點的非勻速直線運動，如果知道的是它在各個時刻的瞬時速度υ (t),要想獲得該質點所在的位置對時間的依賴關係，便歸結到尋求一個函數s(t)，使它的導數恰等於υ(t)。一般地說，對於給定函數ƒ(x), 求出一個或一族（如果運算結果不惟一）函數，使其導數為ƒ(x)的運算稱為積分ƒ(x)。因此，如果積分ƒ(x)的結果是F(x)，則微分F(x)的結果便是ƒ(x)，所以積分是微分的逆運算。
原函數 如果函數F（x）的導數是函數ƒ（x），即，則稱F(x)為ƒ(x)的一個原函數。ƒ(x)的原函數不是惟一的。例如F(x)加上任意常數后，其導數仍然是ƒ(x)。因此重要的事情是弄清楚，ƒ(x)的全體原函數有什麼樣的結構，或者說需要弄清楚ƒ(x)的任何兩個原函數之間的關係。如果F(x)與G(x)都是ƒ(x)的原函數，對函數在某一任意區間上應用微分中值定理可得F(x)-G(x)呏常數，這說明了一個函數的任意兩個原函數之間至多只能相差一個常數。
不定積分與原函數 函數ƒ(x) 的不定積分指的是ƒ(x)的全體原函數，記為。如果已知ƒ(x)的一個原函數F(x)，則有
式中C可以是任意常數。
積分法 求函數的不定積分的一些基本法則。基於積分與微分的互逆關係，將微分公式倒轉順序，便立刻得到一些簡單的積分公式：
相應於複合函數微分法的積分方法是換元積分法。若新舊變數間的關係是是連續函數，則
例如，令，則
令，則
換元積分法擴大了積分公式的使用範圍。
相應於乘積微分公式的積分方法是分部積分法：
求不定積分比求導數要困難得多，即使一些簡單的初等函數，它們的不定積分也不一定能用初等函數的有限形式表達出來。例如等都是“積不出來”的。但這些不定積分仍然可以用其他形式表明自身作為原函數的存在性。
微分和積分的關係 以計算面積為背景的積分運算，從誕生的時候起，就顯示了與微分運算的密切聯繫。牛頓和萊布尼茨首先在幾何上發現了這個事實。如果ƒ(x)是區間上的連續函數，由曲線與x軸及α與x二點的縱坐標線圍成的圖形的面積（圖3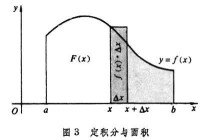
）可以用積分表示。它是x的函數，記作F(x)。當x有一個改變數 Δx，面積F(x) 相應地有一個改變數ΔF(x)。幾何上可以看出，表示ΔF(x)的主要部分的一小塊矩形面積可以是 。對這一事實採用微分的符號來表示，就是
積分學
在此基礎上，得到了聯繫微分與積分的重要定理。
微積分學基本定理 如果函數在區間上連續，則在區間內可微，而且
這就是說，對於任何一個連續函數都有一個可以直接從定積分得到的原函數:因此對於的任意一個原函數，也就總可以表示為比較G(x)在的不同形式，就得到了真正實現定積分計算的公式：
牛頓－萊布尼茨公式這個公式說明在ƒ(x)的一個原函數可以求得的先決條件下（許多情況確實如此），定積分的計算可以轉化為求這個原函數G(x)在兩點的函數值的差。這比直接使用定義去求和、取極限來計算定積分顯然要容易得多。這個公式是微積分學基本定理的直接推論。微積分學基本定理的重要性就在於它把微分與積分從概念上和計算上同時聯繫起來，而成為微積分學形成的理論基礎。
定積分的計算 基於牛頓-萊布尼茨公式，通常應用的方法有換元法和分部積分法。
① 換元法
這裡要求的條件是:ƒ(x)在區間上連續;φ(t)在區間上連續並且適合;φ ′(t)在區間上處處存在並且可積。
② 分部積分法
這裡要求的條件是函數u′，υ′在區間上處處存在並且可積。
定積分的近似計算 由於不少函數的原函數不是初等函數，有些即使是初等函數，其函數值也不一定容易計算，所以在實際計算這些函數的定積分時，往往要考慮通過被積函數來近似計算。近似計算方法的基本思想是：對被積函數進行適當的分划、求和，用有限和來代替積分的真值，並且同時給出這種代替的誤差估計。普通的數值積分方法有：
① 矩形法
其誤差,其中M是在區間上的最大值。
②梯形法
其誤差，其中M是|在區間上的最大值。 ③拋物線法
其誤差,其中M是在區間上的最大值。上述近似公式稱為辛普森公式。
以上三個近似公式中的是等分區間的分點，稱為步長，拋物線法中的n應是偶數。
廣義積分 黎曼積分只是在被積函數有界且積分區間為有窮的限制下定義的。但在應用中有時需要取消這些限制。這就導致廣義積分概念的產生。廣義積分包括無窮積分與瑕積分兩種。
無窮積分 即積分區間為無窮的積分，被定義為正常的黎曼積分的極限：
這裡的條件是ƒ(x)可積及所涉及的極限存在。這時也說相應的無窮積分是收斂的，否則就說是發散的。
瑕積分 相應於函數ƒ(x)在區間的某一端點或某一內點с 附近為無界的情形（該點便稱為函數的瑕點），有
這裡條件也是ƒ(x)可積且所涉及的極限存在。這時也說相應的瑕積分是收斂的，否則就說是發散的。假如函數ƒ(x)在區間上有有限多個瑕點，則可以把這些瑕點當做分點，分別考察ƒ(x)在各個子區間上的瑕積分的收斂性，如果它們都是收斂的，就規定它們的和為原區間上的瑕積分。
廣義積分的收斂性定義與無窮級數的收斂性定義有許多相似之處。例如在無窮積分中，的地位恰如無窮級數中的部分和一樣。符號也如一樣，即表示積分本身，在積分收斂時又表示積分值。在無窮積分與瑕積分中也有絕對收斂與條件收斂的概念以及相應的判別法，這些判別法在原則上也與無窮級數中的那些判別法一致（見級數）。
柯西主值柯西曾結合物理意義提出了積分主值的概念，它的定義是：
積分學
在廣義積分收斂時，積分值等於柯西主值。不過，在廣義積分發散時，柯西主值卻可能存在。例如：
；
。
含參變數積分 黎曼積分與廣義積分的建立，可以提供一種確定並且研究函數的新方法。
假設ƒ(x,t)是一個定義在平面矩形區域上的二元連續函數，考慮它對x在區間【α,b】上的積分，在積分過程中被積函數所依賴的變數t始終保持某一個固定的值。這個積分稱為含參變數t的積分。由於積分值依賴於t而惟一確定，由此可以定義t的一個函數
。
雖然在大多數情況下，這樣確定的函數不是初等函數，但由於它具有定積分的特定形式，仍然可以用來研究這些函數的分析性質。例如，當函數ƒ(x,t)在R 上二元連續時，函數在區間上連續，並且
。
當被積函數ƒ(x，t)關於參變數t的偏導數在R上存在並且連續時，則φ(t)在區間(α ,β)內可微，並且
。
結合廣義積分，可以建立函數含參變數廣義積分。例如，具有無窮上限的含參變數廣義積分，如果對t在其取值區間上的一切參變數值，相應的積分都收斂，則可確定函數
。
相應於函數項級數理論中“一致收斂”的重要概念，含參變數廣義積分對參變數的一致收斂的概念也具有重要意義。
如果對於任意的，存在Aε，當時，對於區間［α ,β］上的一切參量t，不等式
都成立，這時就說含參變數廣義積分在t的區間［α ,β］上一致收斂。
使用一致收斂概念來研究函數φ(t)的分析性質，可得到與含參變數的黎曼積分相似的結論：當函數ƒ(x,t)在區域上二元連續，積分在區間上一致收斂時，函數在區間上連續，並且
。
當ƒ(x,t)在區域x≥α，上二元連續並且具有連續偏導數，同時積分在區間上一致收斂時，函數φ(t)在這個區間上可微，並且
。
對於積分下限為－∞或積分上、下限都為無窮的含參變數的廣義積分和被積函數無界的含參變數的瑕積分，也有類似的結論。
Γ函數是利用含參變數的廣義積分確定一個非初等函數的重要例子。這積分當且僅當s>0時收斂；並且在區間α ≤s≤β上一致收斂，其中α與β為任意兩個正數 。因此函數 Г(s)在任何s>0處都連續。Г函數的一個基本性質是
。
根據這一性質可得到n!的表達式
。
斯特林公式上述表達式由於其中積分對於任何實數都有意義，可用來定義任何一個實數的“階乘”n!，並推導關於一個很大的數階乘的近似估計
。
這個公式被稱為斯特林公式。