方中通
方中通
方中通(1634~1698),字位伯,號陪翁。安徽桐城人(今桐城城關風儀里),明翰林方以智次子。清初著名數學家、天文學家和著作家。哲學家方以智的次子。
他“五歲就傅,九歲入都”。但因李自成攻破北京和清兵入關,“旋遭喪亂,困頓流離”,並曾一度改換姓名,14歲才回到桐城故鄉。以後在方以智隱居五嶺,並屢遭清兵搜捕而到處藏匿期間,方中通差不多隨父一起東奔西走。方以智去世后,他經人介紹,隨佟偉夫到廣東恩平教書十數年,直到垂老。因受家學影響,方中通從小喜愛數學,天文學。先從湯聖弘(六合人、精天文曆法)學習郭守敬《授時歷》,后經薛風祚介紹在南京認識西歐傳教士穆尼閣(1611~1656,波蘭人,首先將對數傳入中國者),並向他學習西方數學知識。
方中通的主要著作是《數度衍》24卷,附1卷,這是他在28歲以前10年間努力的結果。順治十八年(1661年)他在辛丑《數度衍》成一詩中說:”自笑十年忘寢食,寧誇兩手畫方圓”書成之後,他還和學術界友人們不斷地討論書中的問題,加以修改和補訂。此中情況,他在《數度衍》卷首前說得明白:“校閱諸子,不能悉載,同學象數而辯難討論者,則惟揭於子宣(通曆算著《寫天新語》),梅子定九(即梅文鼎),薛子儀甫(清初歷算家著《天步真原》等),湯子聖弘,遊子六(通曆算著《天經或向前後集》),丘子邦士(善算)六君子居多,今皆各有著述為方內所珍重,通謹書其姓氏以志不忘耳。”這裡提到的6個人,都是清初的歷算家,《疇人傳》均有傳可見,《數度衍》雖是方中通所著,但卻包含了諸多學者的思想和論述,是集體研討的產物。康熙二十六年(1687407年),《數度衍》在恩州刊行。《數度衍》篇幅大,內容多。其中卷首《幾何約》1卷(原有3卷,但因“重學解”的原稿被火燒掉了,只剩1卷),是徐光啟譯《幾何原本》前6卷的節本。其它大部分內容則取材於《同文算指》(明李之藻譯本)和《崇禎曆書》,介紹了西方的筆算(納白爾)。籌算和尺算。又在卷十一“少廣”之六內介紹了“倍加隔位合數法”,實則講的是對數。這在中國學者著作中,是第一次論及對數的。關於中國演演算法,則包括在《周髀算經》、《演演算法統宗》和明朝顧應祥的《測圓算術》等書範圍內。
除了球面三角以外,《數度衍》幾乎包羅了當時剛傳入的所有西算知識以及當時所能見及的中算知識,可以稱得上是一部數學上的百科全書。在清初算書奇缺的情況下,它的刊行,無疑對於民間數學知識的傳習,起了積極的影響。
除《數度衍》外,方中通還有多種著作。如《音切衍》2卷、《篆隸辯叢》2卷、《心字宗續編》4卷以及詩文集《陪集》和續集若干卷。另有《周易深淺說》、《四藝略》、《揭方問答》等書稿在康熙二十五年火災中被燒.《數度衍》涉及古今中外知識,“方圓縱橫,窮極其變”,堪稱數學大全。在這本書里他還論及了“對數”,是中國探討“對數”第一人。《數度衍》首卷是“幾何約”,內容是明徐光啟翻譯的《幾何原本》前六卷的節本。這是方中通接觸西方數學之後的著作。另有“珠算”“筆算”“籌算”“尺算”諸法。揭暄是方中通父親方以智的弟子,亦明算術,與之論難日輪大小、光肥影瘦(光的衍射)之故,及古今歲差之不同,別錄為一書,即《揭方問答》。其著作尚有《音韻切衍》、《篆隸辨從》、《心學宗續編》、《陪翁集》等傳世。
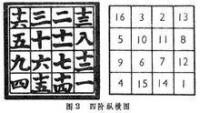
九九圖說
