直線方程
一種數學方程
從平面解析幾何的角度來看,平面上的直線就是由平面直角坐標系中的一個二元一次方程所表示的圖形。求兩條直線的交點,只需把這兩個二元一次方程聯立求解,當這個聯立方程組無解時,兩直線平行;有無窮多解時,兩直線重合;只有一解時,兩直線相交於一點。常用直線向上方向與 X 軸正向的 夾角(叫直線的傾斜角)或該角的正切(稱直線的斜率)來表示平面上直線(對於X軸)的傾斜程度。可以通過斜率來判斷兩條直線是否互相平行或互相垂直,也可計算它們的交角。
直線與某個坐標軸的交點在該坐標軸上的坐標,稱為直線在該坐標軸上的截距。直線在平面上的位置,由它的斜率和一個截距完全確定。在空間,兩個平面相交時,交線為一條直線。因此,在空間直角坐標系中,用兩個表示平面的三元一次方程聯立,作為它們相交所得直線的方程。
空間直線的方向用一個與該直線平行的非零向量來表示,該向量稱為這條直線的一個方向向量。直線在空間中的位置,由它經過的空間一點及它的一個方向向量完全確定。在歐幾里得幾何學中,直線只是一個直觀的幾何對象。在建立歐幾里得幾何學的公理體系時,直線與點、平面等都是不加定義的,它們之間的關係則由所給公理刻畫。
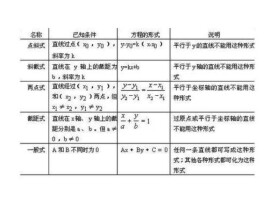
1:一般式:【適用於所有直線】
,
橫截距
縱截距
2:點斜式: 【適用於不垂直於x軸的直線】
表示斜率為k,且過的直線
3:截距式:【適用於不過原點或不垂直於x軸、y軸的直線】
表示與x軸、y軸相交,且x軸截距為a,y軸截距為b的直線
4:斜截式【適用於不垂直於x軸的直線】
表示斜率為k且y軸截距為b的直線
5:兩點式:【適用於不垂直於x軸、y軸的直線】
表示過和的直線
6:交點式:【適用於任何直線】
表示過直線與直線的交點的直線
7:點平式:【適用於任何直線】
表示過點且與直線平行的直線
過原點向直線做一條的垂線段,該垂線段所在直線的傾斜角為α,p是該線段的長度
9:點向式:【適用於任何直線】
表示過點且方向向量為的直線
10:法向式:【適用於任何直線】
表示過點且與向量(a,b)垂直的直線。
點P到直線Ι:的距離
兩平行線之間距離
若兩平行直線的方程分別為:
則
這兩條平行直線間的距離d為:
⑴點關於點對稱的點:
⑵點(x0,y0)關於直線對稱的點:
,
⑶直線關於點對稱的直線:
⑷直線1關於不平行的直線2對稱:定點法、動點法、角平分線法
⑴兩點的對稱點:①求中點坐標
⑵兩點的對稱軸:①求中點坐標②求線段斜率③求與線段垂直的對稱軸斜率④點斜式
⑶兩條平行線的對稱軸:①設P(x,y)在對稱軸上②設方程
⑷兩條相交且不垂直的直線的對稱軸:①角平分線斜率公式②③求交點④點斜式
⑴已知一條直線,與另一條直線相交所成角度為α。
各種不同形式的直線方程的局限性:
(1)點斜式和斜截式都不能表示斜率不存在的直線;
(2)兩點式不能表示與坐標軸平行的直線;
(3)截距式不能表示與坐標軸平行或過原點的直線;
(4)直線方程的一般式中係數A、B不能同時為零。
在自然界和人類社會的各種現象中,同一過程中的變數之間往往存在著一定的關係 .這種關係通常可以分為兩類,一類是在微積分中已經詳細研究過的函數關係,稱為確定性關係;另一類是相關關係,稱為非確定性關係 .研究相關關係的一個有力工具就是回歸分析,它是數理統計的一個重要分支,已經廣泛應用於經濟管理、決策分析、以及自然科學和社會科學等許多研究領域 .回歸分析包括建立回歸直線方程以及利用回歸直線方程進行預測和控制。但是,如果變數不具有近似的線性關係,或者說變數不線性相關,那麼建立的回歸直線方程也失去其價值,預測和控制問題根本就沒有意義。
數理統計中的回歸分析通常是通過所給的樣本數據畫出散點圖,利用最小二乘法估計回歸係數,建立回歸直線方程;通過 F檢驗法、t檢驗法或相關係數檢驗法來檢驗回歸直線方程的顯著性,進而對回歸分析進行預測和控制。如果從相關係數的意義、性質以及相關係數與回歸係數之間的關係入手求回歸直線方程,就省去了畫散點圖,也省去了回歸直線方程的顯著性檢驗,更保證了建立的回歸直線方程有價值,根據相關係數也便於求出回歸係數,進而求出回歸直線方程。
若直線與直線
1. 當時, 相交
2., 平行
3., 重合
4., 垂直
直線:和直線:如果有交點P,
則P的坐標(x,y)為方程組
的解
利用矩陣的旋轉變換,我們可以得出以下的結論:
對於直線l,
①當斜率存在時,直線 繞點 逆時針旋轉α得到的解析式為:
特殊地,當繞的點為原點時,得到的解析式為:
特殊地,當時,得到的解析式為:
特殊地,當,且繞的點為原點時,得到的解析式為:
②當斜率不存在時,直線 繞點 逆時針旋轉α得到的解析式為:
特殊地,當繞的點是原點時,得到的解析式為: