約翰·佩卓
約翰·佩卓
約翰·佩卓(John P. Perdew),美國物理學家,美國科學院院士,國際量子分子科學院院士,天普大學教授。主要研究方向為理論凝聚態物理和量子化學,特別是在密度泛函理論方面作出了卓越的貢獻,這也使他成為世界上被引用率最高的物理學家之一。
John Perdew於1943年8月30日出生於馬里蘭州西部,並在一個叫Cumberland的小城市長大,其父親Paul Perdew和母親Elma Carr Perdew都是教師。在Allegany高中時期,良好的數學課程教會了他“總有方法能夠證明一些事情”的道理。在National Merit Scholarship的獎學金資助下,John Perdew就讀於賓西法尼亞的Gettysburg學院,在那裡他聽到了Richard Mara的精彩課程,這也使他毫不懷疑物理的直覺和數學清晰度可以充分結合成一門學科:物理。
1965-1971年,John在Cornell大學攻讀博士學位。對於大部分年輕人而言,那是一個騷亂的年代;而對John而言也是充滿挑戰性的幾年,他不僅要通過博士學位課程,還要為選定博士論文題目而耗費精力,——為此花了沮喪的幾年時間。在此期間他的論文導師John Wilkins和老師Neil Ashcroft以及David Mermin將其逐漸引入了固體理論領域。在John攻讀博士期間,他們所做的固體體系電子結構計算主要還是沿用Hartree近似,有些其他的物理學家和化學家已經開始試圖探索局域密度或Slater Xα近似了,但在信息傳輸困難的時代,John並沒有獲知這方面的信息。
1965年,Walter Kohn(沃爾特·科恩)和L. J. Sham(沈呂九)首次提出了後來著名的密度泛函理論(Walter Kohn後來因此而獲得了1998年諾貝爾化學獎),而John第一看到這些信息已經是他做博士后的時候了,那是1971-1974年在加拿大的Toronto跟隨Sy Vsoko進行博士后研究期間。
1974-1977年John在Rutgers大學跟隨David Langreth做第二期博士后研究。這時候他確信DFT是一個很精彩的理論,可以基於此做一些提高性的改進和成功的應用。1970年代末,在物理學領域找工作是非常難的,在博士后的後幾年,John每年向外發出數百封求職信,但大部分連面試機會都沒有。作為理論物理出身的人,他當時甚至申請了New Orleans的Tulane大學里一個實驗物理的職位。1977年他被Tulane大學僱用,原因是學校雇一個實驗物理學家的花費太高!

約翰·佩卓
2013年,John Perdew搬到了費城的Temple大學,擔任Laura H. Carnell榮譽教授,並任材料理論中心的創立主任。
John Perdew是世界上被引用率最高的物理學家之一,從2017年的Google Scholar Citations數據來看,他擁有超過23萬次的論文引用,並且仍以每年接近兩萬次的速度增長,H因子為103.一項調查表明,他很可能是1981-2010年間被引用次數最高的物理學家。在300多篇論文中,1996年發表於Physical Review Letters上的關於PBE泛函的文章單篇引用率在8萬次以上,這也是1996-2010年間被引率最高的物理文章。總體來看,Perdew有5篇文章位列過去30年間最高被引的10篇物理學論文。
2003年,國際量子分子科學院院士
2007年,杜蘭大學科學與工程學院傑出研究獎
2009 年,美國化學會Journal of Chemical Theory and Computation雜誌為祝賀Perdew 65歲生日推出專刊
2009 年,杜蘭大學校長獎:傑出學術貢獻及研究生教學
2011年,美國科學院院士
2012年,Materials Theory Award from the Materials Research Society
2015年,John Scott Award
2015年,Alexander von Humboldt Professorship
2015年,布達佩斯技術與經濟大學榮譽博士
John Perdew最廣為人知的學術貢獻是在密度泛函理論(DFT)領域,他首次接觸DFT是在多倫多大學和羅格斯大學做博士後期間,那時DFT還未被廣泛應用,因此他也是這個領域的早期開拓者之一。他使密度泛函在實際計算中可以更加精確,從而在量子化學、材料科學乃至地質學的科學計算中得到廣泛應用。
他的重要貢獻包括:交換相關能中的精確絕熱連接形式,導數不連續性及其對能隙的貢獻,線性標度及其對泛函的精確限制條件,密度泛函的自相互作用修正,非經驗的廣義梯度校正近似(GGA),非經驗的meta-GGA泛函。
Perdew將DFT的泛函劃分為一系列階梯,提出了Jacob階梯方案,用來設計並提高泛函對交換相關能的描述精度。他在2000年的一次國際量化會的DFT專題會上首次提出了這個概念,用以描述五代泛函形式,之後被DFT領域內的其它研究者廣泛採用。
Perdew到天普大學後繼續從事DFT方面的研究,設計了更好的meta-GGA泛函並提高了泛函對強關聯體系及弱關聯體系(范德華力)的描述。
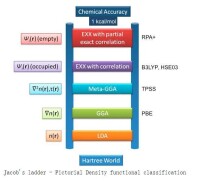
Jacob階梯
Jocob階梯的地面是Hartree理論,是一個非常不精確的方法,既無電子交換能(exchange)也無相關能(correlation). Hartree方法在當今理論化學和物理計算中應用已經很少了。
處於Jacob 階梯最低階的泛函是“局域自旋密度近似”(local spin density approximation, LSDA或LDA). 比如Vosko-Wilk-Nusair (VWN)系列泛函以及1981年John Perdew與Alex Zunger合作提出的Perdew-Zunger (PZ). LDA是對交換相關泛函的最簡單的近似,儘管如此卻比預想的要精確,不過一般來講它會低估原子的基態能量、電離能而高估結合能。LDA對小體系分子效果會差,隨著體系增大效果會變好,應用於密度起伏較小的體系是比較合適的。有的看法認為LDA之所以出乎意料的準確可能是因為它存在一些不足恰好抵消了一些其它錯誤,比如:低估了交換能而又高估了相關能,所以交換相關能恰好達到一個較合適的值。
Jacob 階梯第二階為廣義梯度校正(GGA). 在20世界80年代後期,相繼出現了此種包含電子密度梯度修正的交換相關泛函,這種方法有時也被稱為非局域方法,主要分為兩支流派:第一類更注重經驗性擬合,代表人物是Axel D. Becke;第二類是以John Perdew為代表的更注重從量子力學基本原理推導得來的交換相關泛函。GGA泛函的效果比局域泛函有顯著提高,能給出更好的總能量、原子化能、結構能差以及能壘;不同於LDA傾向於使成鍵效果過強的情況,GGA傾向於高估鍵長(以及晶格常數)。GGA能比較準確地計算共價鍵、離子鍵、金屬體系,但對分子間相互作用的范德華力無能力為,不過近些年來DFT中已經可以加入范德華修正了,Perdew到Temple大學后也與Jianwei Sun合作發展了新的可以描述分子間弱鍵相互作用的新泛函。John Perdew在GGA方面的主要貢獻有:在1991-1992年,與Yue Wang (Perdew的博士生)提出了PW91泛函;1996年與博士后Kieron Burke及Matthias Ernzerhof提出了著名的PBE泛函,該泛函是目前固體結構計算中使用最廣泛的交換相關泛函形式。2008年,Perdew修改了部分PBE參數,讓其更適合固體結構計算,這個泛函稱為PBEsol (PBE for solids).PBEsol可以給出更精確的晶格參數及表面能,對很多固體體系效果很好,鑒於它是對PBE的一個參數改進,所以那些擁有PBE功能的程序都可以很容易地實現PBEsol功能,只需要修改μ和β兩個參數即可。
Jacob階梯第三階泛函統稱為Meta-GGA, 是一種半定域泛函。Meta-GGA在GGA基礎上,將電子動能密度引入泛函形式中,電子動能密度包含了Kohn-Sham佔據軌道的導數。在2003年Jianmin Tao (John Perdew的博士生), John Perdew, Viktor N. Staroverov以及Gustavo E. Scuseria提出了一種較為理想的Meta-GGA泛函TPSS,獲得了廣泛應用。2009年,為了進一步獲得更準確的晶格常數等性質,在TPSS基礎上,Perdew等進一步對TPSS做了改造,得到了RevTPSS (revised TPSS),RevTPSS計算得到的基態幾何結構性質十分的準確,結合能誤差也很小。
Jacob 階梯第四階稱為雜化泛函(Hybird Functional). 它包含了傳統GGA的交換相關部分,同時按一定比例摻雜了Hartree-Fock中的交換部分,因為Hartree-Fock對交換能的計算是精確的。雜化泛函在計算很多分子性質時較GGA有了很大提高,因此在量子化學(尤其是涉及有機化學的計算)中很受歡迎,最典型的雜化泛函是廣泛應用於量子化學計算的B3LYP, 佔據了1990-2006年間量子化學計算中80%的比例;雜化泛函在固體物理中沒有那麼成功,因為基於平面波的固體程序計算精確交換能時會有困難。很多雜化泛函採用了PBE的相關能部分,最著名的有PBE0.
Jacob階梯最高階屬於RPA (Random Phase Approximation)範疇。RPA的概念最早來源於上世紀50年代的量子電動力學(QED)理論,後來逐漸被引入到計算物理及量子化學領域,它可以通過絕熱連接漲落耗散(Adiabatic-connection fluctuation dissipation, ACFD)理論被引入到DFT中。儘管在化學及材料科學中可以擁有非常好的計算效果,但RPA受限於它龐大的計算量,在實際程序中的計算標度增長率一般是O(N)到O(N)量級。
我比John早一年到Tulane大學任教,第一次見到他是在1977年他來求職面試的時候。也許是Walter Kohn對密度泛函理論的預見性吧,那年他來訪問物理系,也因此而預見了(或者說導致了?)John的出現。我來Tulane工作是為了研究密度泛函(DFT),因此也非常慶幸John最後被留下了,我們倆的辦公室在同一層上,相距50英尺。
那個年代,對於來自兩個很小的系裡的人來說,發展密度泛函理論基礎的勝算率幾乎是零。我們頻繁地開一些雖然非正式但是卻很有激情的研討會,成員們也常去聽John所講授的精彩而透徹的密度泛函課。也許是因為我們對這個領域非常沉迷,亦或者說是因為我倆那時都是系裡資歷很淺的職工的原因吧,閑暇時整個五樓上只有我們倆人。我至今還清楚地記得30年前我走進他辦公室跟他分享我第一篇密度泛函理論成果時的情景,他總是在那裡,能夠跟你分享喜悅,能夠給出非常有見地的意見,從不吝嗇出點子。
在那篇著名的Perdew-Zunger自相互作用修正的工作(Phys. ReV. B 1981, 23, 5048)發表幾年後,有一次John非常興奮地跑到我這來說,他得到了一些非常有前景的結果:一個對交換孔的梯度展開的實空間截斷(Phys. ReV. Lett. 1985, 55, 1665). 這個工作修正了二階梯度展開近似(GEA)的一些收斂問題。緊接著,一個關於相關能的文章(Phys. ReV. B 1986, 33, 8822)也做出來了。這兩篇文章奠定了John進入GGA(廣義梯度校正)領域的基礎,我相信GGA這個名詞應該是他創造出來的。——當然,現在做理論計算的人都知道後來的事了。(Mel Levy –杜蘭大學榮休教授,杜克大學訪問教授,國際量子分子科學院院士)

John Perdew與Michael L. Klein
1993年9月,我到Tulane來做John的博士后,那個年代搞凝聚態理論幾乎比70年代更難,我當時已經做了4年博士后了,還一直處在撿別人做剩下的東西的狀態。儘管沒有DFT這塊的經驗,John還是給了我這個工作機會,也令我永遠無比感激。
John當時也有一兩個研究生,不過很長一段時間,我一直是他的第一個博后。他一直很努力地專註於發展DFT:設計新泛函,尋找新的精確條件,解釋失敗原因,發表對論文的錯誤更正,等等等。他的研究組很小,所以能每天都見到我,一般是午飯以及之後的咖啡時間,而每天我幾乎都會問一些很蠢的問題,還經常重複問三四次,但是每天他都無比耐心地給我解釋,甚至還很享受這個過程。三個月後我算是開竅了,問題解決了,結果相當好。
那時候DFT還是個很模糊的學科,只有一小部分忠實信徒在研究,雖然每年三月的美國物理學年會上都會有一個DFT分會場,但都是沒座位的那種屋,DFT的用戶們每次都希望能拿到一些新泛函,但基本都空手而歸。DFT的死忠粉們一般會在那天晚上聚個餐,擠在一張桌子上拚命聊,那會兒經費也不好申,很多人都是自掏腰包來開會的。John當時剛發展了一種廣義梯度校正(GGA)泛函,叫PW91, 然而完全不被主流凝聚態物理研究者們接受,他們更習慣沿用過去的局域密度近似(LDA或S-VWN5),用的程序也都是基於那個檔次的精度來編寫的。我加入John組之後的第一次物理學年會上,簡直出不了會場的門,因為總有人拉住我問為啥他們用GGA時發現效果很差。而我博后的工作就是繼續做這個PW91, 所以根據當時的情況看,這活好像不是很有前景。
同一時間,化學界發生了一場變革,因為化學家們發現GGA和雜化泛函對很多化學現象的解釋精度很高,所以突然之間很多實驗化學家(不僅僅是理論化學家)開始用DFT了。隨著物理和化學兩個學科之間的障礙降低,John開始受邀參加很多化學的會議,我們也開始寫越來越多的材料,——因為John的腦子裡總是有很多想法,而很多時候已發表的一些東西太物理,太模糊,甚至都沒有圖。我們有時候需要給人講明怎麼將這個理論應用到一些模型中,而在這種過程中我們也常常能發現一些新東西。我還記得Matthias Ernzerhof加入組裡后,我們往化學物理雜誌Journal of Chemical Physics上投了一篇文章,結果被審稿人粗暴地拒絕了,後來我們更清晰地解釋了一下我們的目的之後才被接收。
隨著時間的進展,我們發的文章越來越多,比較有趣的一點是我們都很喜歡英語這個語言,投稿的時候不斷地跟編輯打趣。尤其是,John比較喜歡給文章起一些比較好記的題目,比如說,有個我們很喜歡的文章叫” GGAs: A Glance under the Hood”, 這篇就被美國化學會的雜誌給拒了,因為覺得化學家們搜摘要時會認為這篇文章是在討論通風櫥。我們在首字母縮寫問題上也打過敗仗,至少是對那些不以P打頭的來說。(P是John Perdew姓氏的首字母)
我們最廣為人知的工作是一個叫PBE的GGA泛函,這確實是20年來John在GGA領域上不懈努力的巨大勝利和頂峰,它的成功也與一些其它因素有關。其一是Physical Review B當時拒了我們推導PW91的稿子;再者,我對PW91能量密度添加GGA交換相關孔進行參數化時,John突然想出了一個更精確的條件——已經憋了很久了;最後,為了滿足儘可能多的限制條件,John加了一些小的項,只有在梯度很小的時候才成立,而這會給勢能帶來一些問題,從而也不必要地提高了平面波程序的截斷。因此,John希望造一個終極的GGA泛函,這個泛函只包含那些計算所必須的因素,也就是後來的PBE泛函。其實PBE跟PW91很相似,但對凝聚態物理來說,它是一個在正確的時候提出的正確的泛函。楊偉濤教授是眾多從事改進PBE泛函的人中的第一個,我們也很樂意跟他討論他的“強求一致”的困境;丹麥的Hammer和Norskov提出了PBE的修正版RPBE, 也提出了一個重要問題:”PBE or not PBE.”很多人後來都考慮這個問題,包括John自己,所以他又發展了PBEsol泛函。
在我博后時開的最後一次物理學年會上,我很開心地看到Donald R. Hamann(貝爾實驗室一位極其著名的固體理論學家,他說他花了兩周辛苦時間查找並讀了所有的PW91的推導)在大屏幕上向所有所有人解釋,PBE對石英中由壓力引起的相變的解釋是正確的。打那以後,我終於再也不用向物理學家們辯駁PBE的有效性了。
我在Tulane總計做了3年博后,那也是我一生中最高產的時期,John和我以及很多合作者們寫了30多篇文章。那幾年也是最有趣的幾年,——歸功於John的存在,他對每件事的要求都不是那麼苛刻,也允許我們自由發展。我不僅學到了我所需要的所有的DFT知識,也學到了極其重要的寫文章及解釋問題的能力,這也使我在學術界得以混下來。我因此找到了一個職位,雖然是在一個不大的化學系,但很精彩,這是我之前做物理時從沒妄想過的。
