十二平均律

十二平均律，又稱“十二等程律”，是一種音樂定律方法，將一個純八度（如cc）平均分成十二等份，每等分稱為半音，是最主要的調音法。現在的鋼琴就是根據十二平均律定音的。

“十二平均律”的純四度和大三度，兩個音的頻率比分別與4/3和5/4比較接近。也就是說，“十二平均律”的幾個主要的和弦音符，都跟自然泛音序列中的幾個音符相符合的，只有極小的差別，這為小號等按鍵吹奏樂器在樂隊中使用提供了必要條件，因為這些樂器是靠自然泛音級(自然泛音序列，其頻率是基音頻率的整數倍序列，成等差數列)來形成音階的。半音是十二平均律組織中最小的音高距離，全音由兩個半音組成。1-Ⅰ之間分成12份。具體1-2全音，2-3全音，3-4半音，4-5全音，5-6全音，6-7全音，7-i半音。

十二平均律在交響樂隊和鍵盤樂器中得到廣泛使用，鋼琴即是根據十二平均律來定音的，因為只有“十二平均律”才能方便地進行移調。曲調由音階組成，音階由音組成。音有絕對音高和相對音高。聲音是靠振動（聲帶、琴弦等）發出的，而振動的頻率（每秒振動的次數），就決定了的音的絕對高度。不同的音有不同的振動頻率。人們選取一定頻率的音來形成音樂體系所需要的音高。

十二平均律簡而言之，就是把半根琴弦按照等比數列平均分成十二份。一根琴弦的長度設為1，可以表示為(1/2)^(0/12)，第一品的位置是(1/2)^(1/12)，第二品的位置是(1/2)^(2/12)，依此類推，第n品的位置是(1/2)^(n/12)。因為這樣的一組音是等比關係，所以無論從哪個位置開始彈起旋律都是一樣的。

十二平均律的半音，比五度相生律的半音大，比純律小。因此，使用十二平均律奏和弦不純，奏旋律導向性不夠，所以在樂曲的演奏中，尤其在樂隊多聲部合奏的時候，實際上是多律並用的，根據實際情況，在演奏過程中，偏向一種律制，並不是一成不變的。

根據十二平均律所有半音都相等的特點，因此還產生了“等音”。

鋼琴是十二平均律制樂器。國際標準音規定，鋼琴的a1（小字一組的a音，對應鋼琴鍵是49A）的頻率是為440Hz；又規定每相鄰半音的頻率比值為2^(1/12)≈1.059463，（解釋：這表示“2的十二分之一次方”），根據這規定，就可以得出鋼琴上每一個琴鍵音的頻率。如與a1右邊相鄰#a1的頻率是440×1.059463=466.16372Hz；再往上，b1的頻率是493.883213Hz；c2的頻率是523.25099......同理，與a1左邊相鄰的#g1的頻率是440÷1.059463=415.304735Hz.....這種定音的方式就是“十二平均律”。

鋼琴上每相鄰的兩個琴鍵（黑白都算）的頻率的差別，音樂上即為半音。比如說C和#C相差半音，C和D相差兩個半音（或曰一個全音），以此類推。如果B再往上升半音，會發現這個音的頻率剛好是C的兩倍，而在音樂上稱為一個八度，這兩個音聽起來“很相象”。用小寫的c來表示它，依次有#c,d……再往上走可以用c1……，c2……來表示，而往下走可以用大寫的C1……，C2……來表示。

三分損益律、純律、十二平均律，在中國同時存在。因此，也就出現異律並用的情況。在歷史上，南朝宋、齊時清商樂的平、清、瑟三調和隋、唐九、十部樂的清樂中，都是琴、笙與琵琶並用；宋人臨五代周文矩《宮中圖》卷中的琴阮合奏，其時，琴上所用應是純律，笙上所用當為三分損益律，琵琶與阮是平均律。可見，南北朝、隋唐、五代，都存在三律並用的情況。在現存的許多民間樂種中，也有琴、笙、琵琶、阮等樂器的合奏。因此，這種三律並用就成了中國傳統音樂中存在的一。

明朝中葉，皇族世子朱載堉發明以珠算開方的辦法，求得律制上的等比數列，具體說來就是：用發音體的長度計算音高，假定黃鐘正律為1尺，求出低八度的音高弦長為2尺，然後將2開12次方得頻率公比數1.059463094，該公比自乘12次即得十二律中各律音高，且黃鐘正好還原。用這種方法第一次解決了十二律自由旋宮轉調的千古難題。

在朱載堉發表十二平均律理論之後52年，PereMarinMersenne在（1636年）其所著《諧聲通論》中發表相似的理論。

德國作曲家巴赫於1722年發表的《諧和音律曲集》（另或譯為《十二平均律曲集》英文：《The48》），有可能就是為十二平均律的鍵盤樂器所著。

所有的波（包括聲波、電磁波等等）都有三個最本質的特性：頻率/波長、振幅、相位。對於聲音來說，聲波的頻率（聲學中一般不考慮波長）決定了這個聲音有多“高”，聲波的振幅決定了這個聲音有多“響”，而人耳對於聲波的相位不敏感，所以研究音樂時一般不考慮聲波的相位問題。

一般來說，人耳能聽到的聲波頻率範圍是20Hz（每秒振動20次）到20000Hz（每秒振動20000次）之間。聲波的頻率越大（每秒振動的次數越多），聽起來就越“高”。頻率低於20Hz的叫“次聲波”，高於20000Hz的叫“超聲波”。

由於弦樂器是世界各地發展得最早的樂器種類之一，所以這種現象古人早已熟悉。他們自然會想：如果八度音程的2:1的關係在弦樂器上用這麼簡單一按中點的方式就能實現，那麼試試按其它的位置會怎麼樣呢？數學上2:1是最簡單的比例關係了，簡單性僅次於它的就是3:1。那麼，我們如果按住弦的1/3點，會怎麼樣呢？其結果是弦發出了兩個高一些的音。一個音的頻率是原來的3倍（因為弦長變成了原來的1/3），另一個音是原來的3/2倍（因為弦長變成了原來的2/3）。這兩個音彼此也是八度音程的關係（因為它們彼此的弦長比是2:1）。這樣，在我們要尋找的F-2F的範圍內，出現了第一個重要的頻率，即3/2F。（那個3F的頻率正好處於下一個八度，即2F-4F中的同樣位置。）

接著再試，數學上簡單性僅次於3:1的是4:1，我們試試按弦的1/4點會怎樣？又出現了兩個音。一個音的頻率是原來的4倍（因為弦長變成了原來的1/4），這和原來的音（術語叫“主音”）是兩個八度音程的關係，可以不去管它。另一個音的頻率是主音的4/3倍（因為弦長是原來的3/4）。我們又得到了一個重要的頻率，4/3F。同一根弦，在不同的情況下振動，可以發出很多頻率的聲音。在聽覺上，與主音F最和諧的就是3/2F和4/3F（除了主音的各個八度之外）。這個現象也被很多民族分別發現了。比如最早從數學上研究弦的振動問題的古希臘哲學家畢達哥拉斯（Pythagoras，約公元前6世紀）。我國先秦時期的《管子·地員篇》、《呂氏春秋·音律篇》也記載了所謂“三分損益律”。具體說來是取一段弦，“三分損一”，即均分弦為三段，舍一留二，便得到3/2F。如果“三分益一”，即弦均分三段后再加一段，便得到4/3F。

得到這兩個頻率之後，是否繼續找1/5點、1/6點等等繼續試下去呢？不行，因為聽覺上這些音與主音的和諧程度遠不及3/2F、4/3F。實際上4/3F已經比3/2F的和諧程度要低不少了。古人於是換了一種方法。與主音F最和諧的3/2F已經找到了，他們轉而找3/2F的3/2F，即與最和諧的那個音最和諧的音，這樣就得到了（3/2）2F即9/4F。可是這已經超出了2F的範圍，進入了下一個八度。沒關係，不是有“等差音高序列”嗎？在下一個八度中的音，在這一個八度中當然有與它等價的一個音，於是把9/4F的頻率減半，便得到了9/8F。

接著把這個過程循環一遍，找3/2的3次方，於是就有了27/8F，這也在下一個八度中，再次頻率減半，得到了27/16F。

就這樣一直循環找下去嗎？不行，因為這樣循環下去會沒完沒了的。我們最理想的情況是某一次循環之後，會得到主音的某一個八度，這樣就算是“回到”了主音上，不用繼續找下去了。可是（3/2)^n，只要n是自然數，其結果都不會是整數，更不用說是2的某次方。律學所有的麻煩就此開始。

數學上不可能的事，只能從數學上想辦法。古人的對策就是“取近似值”。他們注意到（3/2)^5≈7.59，和2^3=8很接近，於是決定這個音就是他們要找的最後一個音，比這個音再高一點就是主音的第三個八度了。這樣，從主音F開始，我們只需把“按3/2比例尋找最和諧音”這個過程循環5次，得到了5個音，加上主音和4/3F，一共是7個音。這就是為什麼音律上要取do、re、mi等等7個音符而不是6個音符或者8個音符的原因。

這7個音符的頻率，從小到大分別是F、9/8F、81/64F、4/3F、3/2F、27/16F、243/128F。如果這裡的F是do，那麼9/8F就是re、81/64F就是mi……，這7個頻率組成了7聲音階。這7個音都有各自正式的名字，在西方音樂術語中，它們分別被叫做主音（tonic）、上主音（supertonic）、中音（mediant）、下屬音（subdominant）、屬音（dominant）、下中音（submediant）、導音（leadingtone）。其中和主音關係最密切的是第5個“屬音”so和第4個“下屬音”fa，原因前面已經說過了，因為它們和主音的和諧程度分別是第一高和第二高的。由於這個音律主要是從“屬音”so即3/2F推導出來的，而3/2這個比例在西方音樂術語中叫“純五度”，所以這種音律叫做“五度相生律”。西方最早提出“五度相生律”的是古希臘的畢達哥拉斯（所以西方把按3/2比例定音律的做法叫做Pythagoreantuning），東方是《管子》一書的作者（不一定是管仲本人）。我國歷代的各種音律，大部分也都是從“三分損益律”發展出來的，也可以認為它們都是“五度相生律”。

仔細看上面“五度相生律”7聲音階的頻率，可以發現它們彼此的關係很簡單：do-re、re-mi、fa-so、so-la、la-si之間的頻率比都是9:8，這個比例被稱為全音（tone）；mi-fa、si-do之間的頻率比都是256:243，這個比例被稱為半音（semitone）。“五度相生律”產生的7聲音階，自誕生之日起就不斷被批評。原因之一就是它太複雜了。前面說過，如果按住弦的1/5點或者1/6點，得到的音已經和主音不怎麼和諧了，居然出現了81/64和243/128這樣的比例，這不會太好聽吧？於是有人開始對這7個音的頻率做點調整，於是就出現了“純律”（justintonation）。

“純律”的重點是讓各個音盡量與主音和諧起來，也就是說讓各個音和主音的頻率比盡量簡單。“純律”的發明人是古希臘學者塔壬同（今義大利南部的塔蘭托城）的亞理斯托森努斯（AristoxenusofTarentum）。（東方似乎沒有人獨立提出“純律”的概念。）此人是亞理士多德的學生，約生活在公元前3世紀。他的學說的重點就是要靠耳朵，而不是靠數學來主導音樂。他的書籍留下來的只有殘篇，不過可以證實的是他提出了所謂“自然音階”。

自然音階也有7個音，但和“五度相生律”的7聲音階有不小差別。7個自然音階的頻率分別是：F、9/8F、5/4F、4/3F、3/2F、5/3F、15/8F。確實簡單多了吧？也確實好聽多了。這麼簡單的比例，就是“純律”。

可以看出“純律”不光用到了3/2的比例，還用到了5/4的比例。新的7個頻率中和原來不同的就是5/4F、5/3（=5/4×4/3）F、15/8（=5/4×3/2）F。

雖然“純律”的7聲音階比“五度相生律”的7聲音階要好聽，數學上也簡單，但它本身也有很大的問題。雖然各個音和主音的比例變簡單了，但各音之間的關係變複雜了。原來“五度相生律”7聲音階之間只有“全音”和“半音”2種比例關係，如今出現了3種：9:8（被叫做“大全音”，majortone，就是原來的“全音”）、10:9（被叫做“小全音”，minortone）、16:15（新的“半音”）。各位把自然音階的頻率互相除一下就能得到這個結果。更進一步說，如果比較自然音階中的re和fa，其頻率比是27/32，這也不怎麼簡單，也不怎麼好聽呢！所以說“純律”對“五度相生律”的修正是不徹底的。事實上，“純律”遠沒有“五度相生律”流行。

對於“五度相生律”的另一種修正是從另一個方向展開的。還記得為什麼要取7個音符嗎？是因為（3/2)^5≈7.59，和2^3=8很接近。可這畢竟是近似值，而不是完全相等。在一個八度之內，這麼小的差距也許沒什麼，但是如果樂器的音域跨越了好幾個八度，那麼這種近似就顯得不怎麼好了。於是人們開始尋找更好的近似值。通過計算，古人發現（3/2)^12≈129.7，和2^7=128很接近，於是他們把“五度相生律”中“按3/2比例尋找最和諧音”的循環過程重複12次，便認為已經到達了主音的第7個八度。再加上原來的主音和4/3F，如今就有了12個音符。注意，“規範”音階不是do、re、mi……等7個音符了，而是12個音符。這種經過修改的“五度相生律”推出的12聲音階，其頻率分別是：F、2187/2048F、9/8F、19683/16384F、81/64F、4/3F、729/512F、3/2F、6561/4096F、27/16F、59049/32768F、243/128F。

和前面的“五度相生律”的7聲音階對比一下，可以發現原來的7個音都還在，只是多了5個，分別插在它們之間。用正式的音樂術語稱呼原來的7個音符，分別是C、D、E、F、G、A、B。新多出來的5個音符於是被叫做C#（讀做“升C”）、D#、F#、G#、A#。12音階不能用do、re、mi的叫法了，應該被叫做：C、C#、D、D#、E、F、F#、G、G#、A、A#、B。把相鄰兩個音符的頻率互相除一下，就會發現它們之間的比例只有兩種：256:243（就是原來的“半音”，也叫做“自然半音”），2187:2048（這被叫做“變化半音”）。也就是說，這12個音符幾乎可以說又構成了一個“等差音高序列”。它們之間的“距離”幾乎是相等的。（當然，如果相鄰兩個音符之間的比例只有一種的話，就是嚴格的“距離”相等了。）原來的7聲音階中，C-D、D-E、F-G、G-A、A-B之間都相隔一個“全音”，如今則認為它們之間相隔了兩個“半音”。這也就是“全”、“半”這種叫法的根據。

既然C#被認為是從C“升”了半音得到的，那麼C#也可以被認為是從D“降”了半音得到的，所以C#和Db（讀做“降D”）就被認為是等價的。事實上，5個新加入的音符也可以被寫做：Db、Eb、Gb、Ab、Bb。

這種12聲音階在音樂界的地位，我只用舉一個例子就能說明了。鋼琴上的所有白鍵對應的就是原來7聲音階中的C、D……B，所有的黑鍵對應的就是12聲音階中新加入的C#、Eb……Bb。

從7聲音階發展到12聲音階的做法，在西方和東方都出現得很早。《管子》中實際上已經提出了12聲音階，後來的中國音律也大多是以“五度相生律”的12聲音階為主。畢達哥拉斯學派也有提出這12聲音階的。不過西方要到中世紀晚期才重新發現它們。

能不能把“五度相生律”的12聲音階再往前發展一下呢？可以的。12聲音階的依據就是（3/2）^12≈129.7，和2^7=128很接近，按照這個思路，繼續找接近的值就可以了嘛。

還有人真的找到了，此人就是我國西漢的著名學者京房（77BC-47BC）。他發現（3/2）^53≈2.151×10^9，和2^31≈2.147×10^9也很接近，於是提出了一個53音階的新音律。要知道古人並沒有我們的計算器，計算這樣的高次冪問題對他們來說是相當麻煩的。

當然，京房的新律並沒有流行開，原因就是53個音階也太麻煩了吧！開始學音樂的時候要記住這麼多音符，誰還會有興趣哦！但是這種努力是值得肯定的，也說明12聲音階也不完美，也確實需要改進。

“五度相生律”的12聲音階中的主要問題是，相鄰音符的頻率比例有兩種（自然半音和變化半音），而不是一種。而且兩種半音彼此差距還不小。（2187:2048）/（256:243）≈1.014。好像差不多哦？但其實自然半音本身就是256:243≈1.053了。

如果12聲音階是真正的“等差音高序列”的話，每個半音就應該是相等的，各個音階就應該是“等距離”的。也就是說，真正的12聲音階可以把一個八度“等分”成12份。為什麼這麼強調“等分”、“等距離”呢？因為在音樂的發展過程中，人們越來越覺得有“轉調”的必要了。

所謂轉調，其實就是用不同的音高來唱同一個旋律。比方說，如果某一個人的音域是C～高音C（也就是以前的do～高音do），樂器為了給他伴奏，得在C～高音C之內彈奏旋律；如果另一個人的音域是D～高音D（也就是以前的re～高音re），樂器得在D～高音D之內彈奏旋律。可是“五度相生律”的12聲音階根本不是“等差音高序列”，人們會覺得C～高音C之內的旋律和D～高音D之內的旋律不一樣。特別是如果旋律涉及到比較多的半音，這種不和諧就會很明顯。可以說，如果鋼琴是按“五度相生律”來決定各鍵的音高，那麼只要旋律中涉及到許多黑鍵，彈出來的效果就會一塌糊塗。

這種問題在弦樂器上比較好解決，因為弦樂器的音高是靠手指的按壓來決定的。演奏者可以根據不同的音域、旋律的要求，有意地不在規定的指位上按弦，而是偏移一點按弦，就能解決問題。可是鍵盤樂器（比如鋼琴、管風琴、羽管鍵琴等）的音高是固定的，無法臨時調整。所以在西方中世紀的音樂理論里，就規定了有些調、有些音是不能用的，有些旋律是不能寫的。而有些教堂的管風琴，為了應付可能出現的各種情況，就預先準備下許多額外的發音管。以至於有的管風琴的發音管有幾百甚至上萬根之多。這種音律規則上的缺陷，導致一方面作曲家覺得受到了限制，一方面演奏家也覺得演奏起來太麻煩。

問題的根源還是出在近似值上。“五度相生律”所依據的（3/2）^12畢竟和2^7並不完全相等。之所以會出現兩種半音，就是這個近似值造成的。

對“五度相生律”12聲音階的進一步修改，東、西方也大致遵循了相似的路線。比如東晉的何承天（370AD－447AD），他的做法是把（3/2）^12和2^7之間的差距分成12份，累加地分散到12個音階上，造成一個等差數列。可惜這只是一種修補工作，並沒有從根本上解決問題。西方的做法也是把（3/2）^12和2^7之間的差距分散到其它音符上。但是為了保證主音C和屬音G的3/2的比例關係（這個“純五度”是一個音階中最重要的和諧，即使是在12聲音階中也是如此），這種分散註定不是平均的，最好的結果也是12音中至少有一個“不在調上”。如果把差距全部分散到12個音階上的話，就必須破壞C和G之間的“純五度”，以及C和F之間的4/3比例（術語是“純四度”）。這樣一來，雖然方便了轉調，但代價就是音階再也沒有以前好聽了。因為一個八度之內最和諧的兩個關係――純五度和純四度――都被破壞了。

一直到文藝復興之前，西方音樂界通行的律法叫“平均音調律”（Meantonetemperament），就是在保證純五度和純四度盡量不受影響的前提下，把（3/2）^12和2^7之間的差距盡量分配到12個音上去。這種折衷只是一種無可奈何的妥協，大家其實都在等待新的音律出現。

終於還是有人想到了徹底的解決辦法。不就是在一個八度內均分12分嗎？直接就把2:1這個比例關係開12次方不就行了？也就是說，真正的半音比例應該是。如果12音階中第一個音的頻率是F，那麼第二個音的頻率就是F，第三個音就是F，第四個音是F，……，第十二個是F，第十三個就是F，就是2F，正好是F的八度。這是“轉調”問題的完全解決。有了這個新的音律，從任何一個音彈出的旋律可以複製到任何一個其它的音高上，而對旋律不產生影響。西方巴洛克音樂中，復調音樂對於多種聲部的偏愛，有了這個新音律之後，可以說不再有任何障礙了。後來的古典主義音樂，也間接地受益匪淺。可以說沒有這個新的音律的話，後來古典主義者、浪漫主義者對於各種音樂調性的探索都是不可能的。

這種新的音律就叫“十二平均律”。首先發明它的是一位中國人，叫朱載堉（yù）。他是明朝的一位皇室後代，生於1536年，逝世於1611年。他用珠算開方的辦法（珠算開12次方，難度可想而知），首次計算出了十二平均律的正確半音比例，其成就見於所著的《律學新書》一書。很可惜，他的發明，和中國古代其它一些偉大的發明一樣，被淹沒在歷史的塵埃之中了，很少被後人所知。

西方人提出“十二平均律”，大約比朱載堉晚50年左右。不過很快就傳播、流行開來了。主要原因是當時西方音樂界對於解決轉調問題的迫切要求。當然，反對“十二平均律”的聲音也不少。主要的反對依據就是“十二平均律”破壞了純五度和純四度。不過這種破壞程度並不十分明顯。

“十二平均律”的12聲音階的頻率（近似值）分別是：F（C）、1.059F（C#/Db）、1.122F（D）、1.189F（D#/Eb）、1.260F（E）、1.335F（F）、1.414F（F#/Gb）、1.498F（G）、1.587F（G#/Ab）、1.682F（A）、1.782F（A#/Bb）、1.888F（B）。

注意，所有的半音都一樣了，都是，即1.059。以前的自然半音和變化半音的區別沒有了。另外，原來“五度相生律”的12音階中，C和G的比例是3/2（即純五度），“十二平均律”的12音階中，C和G的比例是1.498，和純五度所要求的3/2（1.5）非常接近。原來“五度相生律”的12音階中，C和F的比例是4/3（即純四度），“十二平均律”的12音階中，C和F的比例是1.335，和純四度所要求的4/3（1.333）也非常接近。所以“十二平均律”基本上保留了“五度相生律”最重要的特性。又加上它完美地解決了轉調問題，所以後來“十二平均律”基本上取代了“五度相生律”的統治地位。鋼琴就是按“十二平均律”來確定各鍵音高的。學生們學習的do、re、mi也是按“十二平均律”修改過的7聲音階。如果想聽“五度相生律”或者“純律”的do、re、mi，已經很不容易了。

將八度音等分為十二等分，其數學意義如下：

八度音指的是頻率加倍（即二倍頻率）。因此在八度音中分為十二等分乃是分為十二個等比級數，其結果就是每個音的頻率為前一個音的2開12次方倍（）。

十二平均律中各音的頻率（0.00001Hz）

C4:261.62557Hz

#C4:277.18263Hz

D4:293.66477Hz

#D4:311.12698Hz

E4:329.62756Hz

F4:349.22823Hz

#F4:369.99442Hz

G4:391.99544Hz

#G4:415.30470Hz

A4:440.00000Hz

#A4:466.16376Hz

B4:493.88330Hz

C5:523.25113Hz

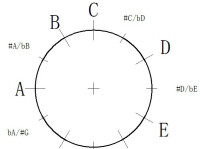
理論上來說，所有樂器的音準只需要儀器來校準。但是實踐證明，十二平均律僅僅在中低頻率適用於人對音階感覺，當頻率較高時（往往大於1500Hz），人感覺上的音階較實際計算的十二平均律偏高，所以樂器的調音師是不可被儀器替代的。為了聲音的協和，實際上鋼琴各個鍵的音高也並不是嚴格按照十二平均律來調音的，在中音區，嚴格按照十二平均律來調音；在高音區，傾向於五度相生律，即半音變小；在低音區，傾向於純律，半音變寬（音程的大小也就是兩個音高的比值，從鋼琴的調音曲線上看，高音區音高偏高，低音區偏低，這是為了使聲音協和，高音半音減小，低音半音增大，分數的分子和分母同時增大或較小，會引起比值減小或增大，引起半音發生變化，從物理意義上說，主要是琴弦兩端的約束造成的）。

正式的交響樂校音的基本a1的頻率往往不是440Hz，為了讓音樂更為明亮，交響樂的基準頻率一般會提高至442Hz左右。