徑向基函數網路
1988年洛維等建立的神經網路
在數學建模領域,徑向基函數網路(Radial basis function network,縮寫:RBF network)是一種使用徑向基函數作為激活函數的人工神經網路。徑向基函數網路的輸出是輸入的徑向基函數和神經元參數的線性組合。徑向基函數網路具有多種用途,包括包括函數近似法、時間序列預測、分類和系統控制,最早由布魯姆赫德(Broomhead)和洛維(Lowe)在1988年建立。
在介紹徑向基網路之前,先簡單介紹一下徑向基函數(Radical Basis Function,RBF)。徑向基函數(Radical Basis Function,RBF)方法是Powell在1985年提出的。所謂徑向基函數,其實就是某種沿徑向對稱的標量函數。通常定義為空間中任一點x到某一中心c之間歐氏距離的單調函數,可記作,其作用往往是局部的,即當x遠離c時函數取值很小。例如高斯徑向基函數:
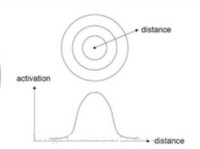
圖1 高斯徑向基函數
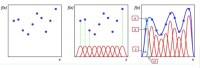
圖2 徑向基函數模擬插值過程
RBF網路的結構與多層前向網路類似,它是一種三層前向網路。輸入層由信號源結點組成;第二層為隱含層,隱單元數視所描述問題的需要而定,隱單元的變換函數是RBF徑向基函數,它是對中心點徑向對稱且衰減的非負非線性函數;第三層為輸出層,它對輸入模式的作用作出響應。從輸人空間到隱含層空間的變換是非線性的,而從隱含層空間到輸出層空間變換是線性的。
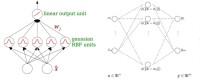
徑向基函數網路
當RBF的中心點確定以後,這種映射關係也就確定了。而隱含層空間到輸出空間的映射是線性的,即網路的輸出是隱單元輸出的線性加權和,此處的權即為網路可調參數。由此可見,從總體上看,網路由輸人到輸出的映射是非線性的,而網路輸出對可調參數而言卻又是線性的。這樣網路的權就可由線性方程組直接解出,從而大大加快學習速度並避免局部極小問題。
從另一個方面也可以這樣理解,多層感知器(包括BP神經網路)的隱節點基函數採用線性函數,激活函數則採用Sigmoid函數或硬極限函數。而RBF網路的隱節點的基函數採用距離函數(如歐氏距離),並使用徑向基函數(如Gaussian函數)作為激活函數。徑向基函數關於n維空間的一個中心點具有徑向對稱性,而且神經元的輸入離該中心點越遠,神經元的激活程度就越低。隱節點的這一特性常被稱為“局部特性”。
RBF的設計主要包括兩個方面,一個是結構設計,也就是說隱藏層含有幾個節點合適。另一個就是參數設計,也就是對網路各參數進行求解。由上面的輸入到輸出的網路映射函數公式可以看到,網路的參數主要包括三種:徑向基函數的中心、方差和隱含層到輸出層的權值。到目前為止,出現了很多求解這三種參數的方法,主要可以分為以下兩大類:
通過非監督方法得到徑向基函數的中心和方差,通過監督方法(最小均方誤差)得到隱含層到輸出層的權值。具體如下:
(2)RBF神經網路的基函數為高斯函數時,方差可由下式求解:
式中 為所選取中心之間的最大距離,h是隱層節點的個數。擴展常數這麼計算是為了避免徑向基函數太尖或太平。
(3)隱含層至輸出層之間神經元的連接權值可以用最小均方誤差LMS直接計算得到,計算公式如下:(計算偽逆)(d是我們期待的輸出值)
採用監督學習演演算法對網路所有的參數(徑向基函數的中心、方差和隱含層到輸出層的權值)進行訓練。主要是對代價函數(均方誤差)進行梯度下降,然後修正每個參數。具體如下:
(1)隨機初始化徑向基函數的中心、方差和隱含層到輸出層的權值。當然了,也可以選用結構設計中的(1)來初始化徑向基函數的中心。
(2)通過梯度下降來對網路中的三種參數都進行監督訓練優化。代價函數是網路輸出和期望輸出的均方誤差:
然後每次迭代,在誤差梯度的負方向已一定的學習率調整參數。