混沌現象
指發生在確定性系統中的貌似隨機不規則運動
混沌現象是指發生在確定性系統中的貌似隨機的不規則運動,一個確定性理論描述的系統,其行為卻表現為不確定性一不可重複、不可預測,這就是混沌現象。
混沌現象是指發生在確定性系統中的貌似隨機的不規則運動,一個確定性理論描述的系統,其行為卻表現為不確定性、不可重複、不可預測,這就是混沌現象。進一步研究表明,混沌是非線性動力系統的固有特性,是非線性系統普遍存在的現象。牛頓確定性理論能夠充分處理的多為線性系統,而線性系統大多是由非線性系統簡化來的。因此,在現實生活和實際工程技術問題中,混沌是無處不在的。
“混沌”是近代非常引人注目的熱點研究,它掀起了繼相對論和量子力學以來基礎科學的第三次革命。科學中的混沌概念不同於古典哲學和日常語言中的理解,簡單地說,混沌是一種確定系統中出現的無規則的運動。混沌理論所研究的是非線性動力學混沌,目的是要揭示貌似隨機的現象背後可能隱藏的簡單規律,以求發現一大類複雜問題普遍遵循的共同規律。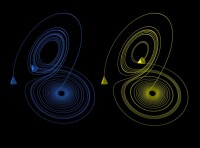

混沌現象
1963年,Lorenz(中文名譯作洛倫茲)在《大氣科學》雜誌上發表了“決定性的非周期流”一文,指出在氣候不能精確重演與長期天氣預報者無能為力之間必然存在著一種聯繫,這就是非周期與不可預見性之間的聯繫。他還發現了混沌現象“對初始條件的極端敏感性”。這可以生動的用“蝴蝶效應”來比喻:在做氣象預報時,只要一隻蝴蝶扇一下翅膀,這一擾動,就會在很遠的另一個地方造成非常大的差異,將使長時間的預測無法進行。
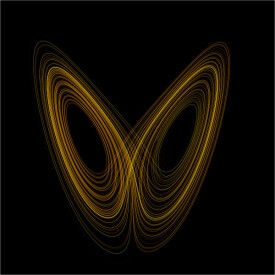
在60年代研究的基礎上,混沌學的研究開始進入高潮。1971年,科學家在耗散系統中正式的引入了奇異吸引子的概念(如Henon吸引子[見圖(1-1)]、Lorenz吸引子[見圖(2-2)]。1975年,李天岩和J.A.Yorke和提出了混沌的科學概念。整個70年代中期,人們不但在理論上對混沌做更深層次的研究,而且努力在實驗室中找尋奇異吸引子。李天岩和J.A.Yorke在他們的著名論文“周期3意味著混沌”中,指出:在任何一維繫統中,只要出現周期3,則該系統也能出現其他長度的周期,也能呈現完全的混沌。
在確定性的系統中發現混沌,改變了人們過去一直認為宇宙是一個可以預測的系統的看法。用決定論的方程,找不到穩定的模式,得到的卻是隨機的結果,徹底打破了拉普拉斯決定論式的可預測性的幻想。但人們同時發現到過去許多曾被認為是雜訊的信號,其實是一些簡單的規則生成的。這些包含內在規則的“雜訊”不同於真正的雜訊,它們的這種規則是完全可以應用的。
對於什麼是混沌,目前科學上還沒有確切的定義,但隨著研究的深入,混沌的一系列特點和本質的被揭示,對混沌完整的、具有實質性意義的確切定義將會產生。目前人們把混沌看成是一種無周期的有序。它包括如下特徵:
它雖然貌似雜訊,但不同於雜訊,系統是由完全確定的方程描述的,無需附加任何隨機因數,但系統仍會表現出類似隨機性的行為;
前面提到的lorenz吸引子,Henon吸引子都具有分形的結構;
是一種無周期的有序。在由分岔導致混沌的過程中,還遵從Feigenbaum常數系。
只要初始條件稍有偏差或微小的擾動,則會使得系統的最終狀態出現巨大的差異。因此混沌系統的長期演化行為是不可預測的。
傳統上,人們把信號分為兩大類:
l確定性信號這種信號所有時刻的波形都是確定的;
l隨機過程它的波形由概率分佈確定。
然而,這樣的分類忽略了另一類極為重要的信號——混沌信號。混沌信號的波形是非常不規則的,表面上看來就象雜訊,但實際上它卻是由確定性的規則所產生的,這種規則有時是很簡單的。正是這種簡單的規則產生出複雜的波形激發了人們對它極大的興趣。在圖(1-2)中,我們向大家展示了由Logistic映射所生成的混沌信號與白雜訊信號,從表面上我們是無法判斷出雜訊與混沌的。讓人興奮的是:實踐證明,在大量的物理系統和自然系統中都存在著混沌信號!雖然,混沌現象的出現使我們無法對系統的長期行為進行預測,但是我們完全可以利用混沌的規律對系統進行短期的行為預測,這樣比傳統的統計學方法更加有效。
此外,人類語言具有混沌現象。上世紀80年代,學術界開始採用混沌論來研究語言問題。1991年在美國伯克利舉行的“語言研究的新方法與新視野”研討會上,中國數學家、語言學家周海中教授曾建議創立“語言混沌論”。他指出,語言混沌論主要從混沌論的角度審視語言及其相關現象,運用混沌論的方法解決語言及其相關現象的非線性問題;為了促進混沌語言研究的發展,有必要建立一種新型的語言研究範式。就目前情況來看,這種語言研究新範式正在興起。
生成類似雜訊的混沌信號
從某種現象中檢測混沌信號是否存在。
檢測到混沌現象的存在,對我們更深刻的認識系統的特徵是極為有利的。在大多數情況下,當我們確認系統中存在混沌時,我們可以利用混沌學的原理,將混沌信號從有用的信號中濾除,從而達到改善信噪比的結果,而這用傳統的濾波方法有時或許是無效的。
天然存在的系統(物理系統、化學系統或生物系統)能呈現混沌,這一點目前已得到普遍共識,並引起了許多學者在實驗室里或在自然狀況下對混沌識別進行嘗試。然而在實驗系統里,雜訊會與決定系統演化的內在方程所支配的動力學特性發生相互作用,故實驗系統肯定會有隨機輸入,從而給混沌的識別帶來了許多困難。下面我們簡要的介紹現今用來識別混沌的幾種不同的方法。
最為人們所熟識且應用最多的一種表徵複雜時間序列特性的統計量是功率譜(powerspectrum),它把複雜的時間序列分解成不同頻率的正弦振蕩的疊加。在給定頻率處的功率譜值與頻率的正弦波係數的平方成正比。典型的功率譜由一個或多個尖峰,它們對應於信號中出現的主要頻率。除這些主峰外,其他頻率也可能出現,不過幅度較低,而且功率譜通常分佈在一個寬頻帶上。
寬頻帶功率譜(多半具有疊加尖峰)往往與混沌動態相聯繫。但不幸的是,“雜訊”也與寬頻譜密切相關,因而出現寬頻譜並不足以確認與雜訊相對的混沌。
混沌的產生是系統整體穩定性和局部不穩定性共同作用的結果,局部的不穩定性使它具有對初值的敏感性,而整體的穩定性則使它在相空間(又稱狀態空間)表現出一定的分形結構,這種結構被稱為混沌吸引子。正是這種精密的吸引子結構,使我們可以利用它來達到分辨雜訊與混沌的目的,因為真正的雜訊在相空間中仍然表現出一團糟的情況。相空間重構技術是一種簡單而實用的技術,但它依然有著極大的局限性。這是因為使用相空間技術來觀察吸引子的結構,依靠的是人眼的辨別,當吸引子的維數高於三維時,我們將束手無策。另外,並非所有的混沌現象都存在著混沌吸引子(如Logist映射)。
有關非線性動力學的研究工作已提出了一些定量刻劃複雜動力學性態的量度。其中兩個最常用的量是李雅譜諾夫指數(LyapunovExponent)和維數(Dimension),它們分別量度動力學性態的規則性程度和幾何結構。李雅譜諾夫指數描述了系統軌跡收斂或發散的比率,當一個系統中同時存在正的和負的李雅譜諾夫指數時,便意味著混沌的存在。事實上李雅譜諾夫指數的重要作用之一就是判斷系統的混沌行為。我們這裡的維數是指的混沌吸引子所具有的分數維維數。在相空間中維數反映描述了在相空間中運動所需要的不多不少的變數個數,而在吸引子中維數則說明了刻畫該吸引子所必需的信息量。