黎曼幾何學
波恩哈德·黎曼提出的理論
德國數學家(G.F.)B.黎曼在19世紀中期所提出的幾何學理論。1854年,他在格丁根大學發表的就職演說,題目是《論作為幾何學基礎的假設》,可以說是黎曼幾何學的發凡。

黎曼幾何學
德國數學家(G.F.)B.黎曼在19世紀中期所提出的幾何學理論。1854年,他在格丁 根大學發表的就職演說,題目是《論作為幾何學基礎的假設》,可以說是黎曼幾何學的發凡。從數學上講,他發展了空間的概念,首先認識到幾何學中所研究的對象是一種"多重廣延量",其中的點可以用n個實數作為坐標來描述,即現代的微分流形的原始形式,為用抽象空間描述自然現象打下了基礎。更進一步,他認為,通常所說的幾何學只是在當時已知測量範圍之內的幾何學,如果超出了這個範圍,或者是到更細層次的範圍裡面,空間是否還是歐幾里得的則是一個需要驗證的問題,需要靠物理學發展的結果來決定。他認為這種空間(也就是流形)上的幾何學應該是基於無限鄰近點之間的距離。在無限小的意義下,這種距離仍然滿足勾股定理。這樣,他就提出了黎曼度量的概念。這個思想發源於C.F.高斯。但是黎曼提出了更一般化的觀點。在歐幾里得幾何中,鄰近點的距離平方是 這確定了歐幾里得幾何。但是在一般曲線坐標下,則應,這是相當特殊的一組函數。如果是一般的函數,又(gij)仍構成正定對稱陣,那麼出發,也可以定義一種幾何學,這便是黎曼幾何學。由於在每一點的周圍,都可以選取坐標使得在這點成立,所以在非常小的區域裡面勾股定理近似成立。但在大一點的範圍里一般就和歐幾里得幾何學有很大的區別了。
黎曼認識到距離只是加到流形上的一個結構,因此在同一
其後,E.B.克里斯托費爾、G.里奇等人又進一步發展了黎曼幾何,特別是里奇發展了張量分析的方法,這在廣義相對論中起了基本的作用。1915年A.愛因斯坦創立了廣義相對論,使黎曼幾何在物理中發揮了重大的作用,對黎曼幾何的發展產生了巨大的影響。廣義相對論真正地用到了黎曼幾何學,但其度量形式不是正定的,現稱為洛倫茨流形的幾何學(見廣義相對論)。
廣義相對論產生以來,黎曼幾何獲得了蓬勃的發展,特別是É.嘉當在20世紀20~30年代開創並發展了外微分形式與活動標架法,建立起李群與黎曼幾何之間的聯繫,從而為黎曼幾何的發展奠定了重要基礎且開闢了廣闊的園地,影響極為深遠,由此還發展了線性聯絡及纖維叢方面的研究。半個多世紀以來,黎曼幾何的研究也已從局部發展到整體,產生了許多深刻的並在其他數學分支和現代物理學中有重要作用的結果。隨著60年代大範圍分析的發展,黎曼幾何和偏微分方程(特別是微分運算元的理論)、多複變函數論、代數拓撲學等學科互相滲透、互相影響。在現代物理中的規範場理論(又稱楊-米爾斯理論)中,黎曼幾何也成了一個有力的工具。
公式
黎曼幾何是黎曼流形上的幾何學。黎曼流形指的是一個n維微分流形M,在其上給定了一個黎曼度量g,也就是說,在微分流形M的每一個坐標鄰域(U,x)內,用一個正定對稱的二次微分來度量二個無限鄰近的點(x1,x2,…,xn)和(x 1+dx1,x2+dx2,…,xn+dxn)之間的距離。這裡(gij)構成一個正定對稱的n×n陣,並假設gij(x)關於(xi)有一定的可微性,而M上連接兩點P、Q的曲線C:xi=xi(t),α≤t≤b的長度l(C) 就用積分來計算。為了保證距離的度量與坐標鄰域的選取無關,還要求gij滿足二階協變張量的變換規律,用整體黎曼幾何的語言來說,就是在微分流形M上給定了一個由分量gij決定的正定對稱二階協變張量場g。M連同g,即(M,g)稱為一個n維黎曼流形,g稱為度量張量或基本張量。由於歷史的原因,黎曼流形又常稱黎曼空間,但後者偏重於局部意義,即常指黎曼流形的一個開子集或一個坐標鄰域。
公式
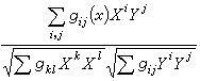
公式
公式
度量張量g在流形M每點 P(x1,x2,…,xn)的切空間Tp(M)中就規定了一個內積gp( 或記為:〈,〉)用來計算切向 量的長度、交角。即若向量X,Y∈Tp(M),而,,則X 的長度;X、Y的交角 θ由,0≤θ≤π決定。如果cosθ=0,即,就稱X、Y 為互相正交。│尣│=1的向量稱為單位向量,Tp(M)中由兩兩互相正交的單位向量組成的基稱為正規正交基,對任一點P∈M,在P點的某一鄰域U 內總存在n個單位向量場e1,e2,…,en,使得在U的每點它們構成切空間的一個正規正 交基,這n個局部向量場稱為一個局部正規正交基或局部正規正交標架。運用局部正規正交標架來研究 黎曼幾何的方法稱為活 動標架法。黎曼幾何中的許多公式和幾何量在活動標架下有特別簡單明了的表達式,例如取ω1,ω2,…,ωn為局部正規正交標架e1,e2,…,en的對偶形式,也稱對偶基,即滿足的n個一次微分形式,於是在基{ei}下,由於,度量形式可寫為。
任一仿緊微分流形總具有黎曼度量,這種黎曼度量的數目是非常繁多的,但也不是完全任意的。微分流形的度量結構是受它的拓撲結構所制約的,而這種制約關係正是黎曼幾何研究的一個重要內容,還存在許多沒有解決的問題。
有了計算曲線長度的方法,黎曼流形(M,g)上任意兩點 P、 Q之間的距離d( P, Q)就可以用M中連接 P、 Q的所有分段可微分曲線的長度的下確界來定義,即(連接 P, Q的分段可微分曲線 C)。於是,M在上述距離下成為一個度量空間,還可以證明,它所導出的度量拓撲與流形M原有的拓撲是等價的。

黎曼幾何學
黎曼幾何學