正交變換群
正交變換群
正交變換群(orthogonal transformation group)亦稱運動群或度量群,簡稱正交群,是一類基本的變換群,即全體正交變換所構成的變換群。例如,平面上全體正交變換的集合構成平面上的正交群,空間中正交變換的全體構成空間中的正交群,平面上(空間中)的正交群是平面上(空間中)仿射群的子群,研究正交群下不變性質與不變數的幾何稱為歐氏幾何或度量幾何。
歐氏平面內的所有正交變換的集合構成群。
證明:
(1)封閉性:設是兩個正交變換,它們的係數方陣分別為,則的係數方陣為
根據方陣的乘法法則,我們有:
但
所以
因此仍是正交變換。
因為,所以,故,所以
因此其逆變換仍是正交變換。
由(1)(2)可得正交變換構成群。
正交變換就是運動,可以說所謂歐氏幾何就是正交變換群下的幾何。即,研究在正交變換之下有那些不變的性質和不變的量。由正交變換的定義,“距離”是基本的不變數,由此可以推出一系列其他的不變性叫不變數。 · ·正交變換把任意圖形F變成與它合同的圖形F‘,但正交變換是構成群的,因此圖形的合同關係具有下列性質: ·
1)圖形F與自身常合同(反身性),恆等變換保證了這一性質。
2)如果圖形F合同於F‘,則圖形F’也合同於F(對稱性),逆變換保證了這一性質。
3)如果圖形F合同於圖形F,圖形F合同於圖形F,則圖形F合同於圖形F(傳遞性),變換積保證了這一性質。
因此,圖形的合同關係是一個等價關係。按著這—關係可將平面、(空間)內的所有圖形進行分類,凡是合同的圖形都屬於同一個等價類,其中所有的圖形都具有共同的幾何性質,它們是正交變換下的不變性質;反過來,正交變換下的不變性質,也正是同一等價類圖形的共同性質。
正交變換的幾何就是研究正交變換下各等價類的共同性質,也就是正交變換下圖形的不變性質和不變數。例如結合關係、順序關係、合同關係、度量關係、平行關係,而這些關係都是歐幾里得公理系統的推論,具體地說,這些不變性質和不變數也就是屬於,介於、相交、平行、垂直、合同、角、正多邊形、相似形、圓和其它二次曲線,長度、面積等,以及把這平面幾何的性質推廣到空間的一些性質等等,它們都是歐氏幾何所研究的幾何性質和量。可見,正交變換群的幾何學就是歐氏幾何學。
正交變換的定義和簡單性質
定義 平面上(或空間中)保持兩點間距離不變的變換,叫做正交變換。
顯然,運動是正交變換。
正交變換有下列性質:
(1)兩個正交變換的乘積是正交變換,正交變換的逆變換還是正交變換,這些都不難用正交變換的定義驗證,容易看出正交變換的全體構成一個群,叫做正交變換群。
(2)正交變換把直線變成直線,為此,我們只需要證明,正交變換把共線的三點變成共線的三點.設P、Q、R是平面上順序的三點,那麼,它們在同一直線上的充要條件是:。因為正交變換保持距離不變,所以變換之後,這個等式仍然成立,因此還在一條直線上。
利用上面的事實可以證明,空間中的正交變換還把平面變成平面。
(3)正交變換把相交直線(或平面)變成相交直線(或平面),平行直線(或平面)變成平行直線(或平面)。
平行直線(或平面)沒有公共點,它們經過正交變換之後,根據變換是一一的和性質(2),仍然變成沒有公共點的直線(或平面),即仍舊是平行直線(或平面) 。
(4)正交變換保持線段的分比不變。
由正交變換保持距離不變這一事實即可推出。
由性質(4)和(2),正交變換把線段變成線段,因為線段上的任意點把線段分成定比A,經過正交變換,A保持不變,所以線段上的點仍變成線段上的點,由此推出線段變成線段。
(5)正交變換保持角度不變。
實際上,設(A、B是在角兩邊上任取的點)在正交變換下變成。因為正交變換保持距離不變,所以與的對應邊相等,於是
因此
因為正交變換即保持距離又保持角度不變,因此它把直角坐標系變為直角坐標系(圖1)。
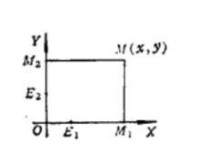
圖1
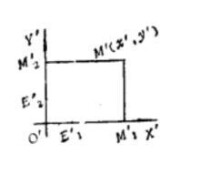
圖2
設點M的坐標為(x,y),因為正交變換保持分比不變,因而有
這表明M'在變換后的坐標系中的坐標與M在原坐標系中的坐標相同。其中,E、E分別是X軸與Y軸上的單位點;M、M分別是M在X軸與Y軸上的正投影。
對於空間的正交變換,也有同樣的結果。