四次函數

數學中的概念

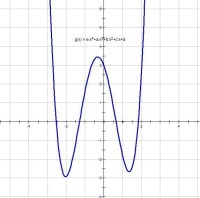
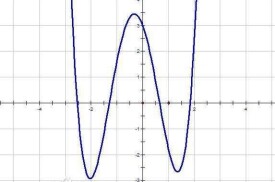
形如y=ax+bx+cx+dx+e(a≠0，b，c，d，e為常數)的函數叫做四次函數。四次函數的圖像成一般W形。一般的四次方程還可以待定係數法解，這種方法稱為笛卡爾法，由笛卡爾於1637年提出。

目錄

1函數解法一般解法與四次函數的關係

待定係數法四次方程解法 2函數圖像

3函數情況一般情況特殊情況

函數解法

一般解法

四次函數的圖像

四次函數的圖像

a*x^4+b*x^3+c*x^2+b*x+a=0的求解方法，對於一般的四次方程a*x^4+b*x^3+c*x^2+d*x+e=0，先求解三次方程8y^3-4cy^2+(2bd-8e)y+e(4c-b^2)-d^2=0，得到的y的任一實根分別代入下面兩個方程：

及x^2+(b-sqrt(8y+b^2-4c))x/2+(y-(by-d)/sqrt(8y+b^2-4c))=0

就可得到原方程的四個根。

與四次函數的關係

在數學中，一元四次方程是令四次函數等於零的結果，這是因為：

假定y=ax+bx+cx+dx+e為目標函數

令y=0

則ax+bx+cx+dx+e=0 （1）

（1）正好是一個一元四次方程。

代數基本定理告訴我們，一個一元四次方程總有四個解（根）。它們可能是複數，也可能存在兩個以上的根相等的情況。具體情況如下：

費拉里法

方程兩邊同時除以最高次項的係數可得 x^4+bx^3+cx^2+dx+e=0 (1)

移項可得 x^4+bx^3=-cx^2-dx-e (2) 兩邊同時加上(1/2bx)^2 ，可將（2）式左邊配成完全平方式，

方程成為 (x^2+1/2bx)^2=(1/4b^2-c)x^2-dx-e (3)

在（3）式兩邊同時加上(x^2+1/2bx)y+1/4y^2

可得 [(x^2+1/2bx)+1/2y]^2= (1/4b^2-c+y)x^2+(1/2by-d)x+1/4y^2-e (4)

（4）式中的y是一個參數。當（4）式中的x為原方程的根時，不論y取什麼值，（4）式都應成立。

特別，如果所取的y值使（4）式右邊關於x的二次三項式也能變成一個完全平方式，則對（4）對兩邊同時開方可以得到次數較低的方程。為了使（4）式右邊關於x的二次三項式也能變成一個完全平方式，只需使它的判別式變成0，即 (1/2by-d)^2-4(1/4b^2-c+y)(1/4y^2-e)=0 (5)

這是關於y的一元三次方程，可以通過塔塔利亞公式來求出y應取的實數值。

把由（5）式求出的y值代入（4）式后，（4）式的兩邊都成為完全平方，兩邊開方，可以得到兩個關於x的一元二次方程。

解這兩個一元二次方程，就可以得出原方程的四個根。

費拉里法經過簡化后，實際上可以這樣表述：

先將一元四次方程化為x+bx+cx+dx+e=0

此方程是以下兩個一元二次方程的解：

2x+(b+M)x+2(y+N/M)=0

2x+(b-M)x+2(y-N/M)=0

其中

M=；N=by-d，（M≠0）

y是一元三次方程8y-4cy-(8e-2bd)y-e(b-4c)-d=0的任一實根。

待定係數法

待定係數法又稱為笛卡爾法

先將四次方程化為x^4+ax^3+bx^2+cx+d=0的形式。

令x=y-a/4 整理后得到y^4+py^2+qy+r=0 （1）

設y^4+py^2+qy+r=(y^2+ky+t)(y^2-ky+m)=y^4+(t+m-k^2)y^2+k(m-t)y+tm

比較dy對應項係數，得t+m-k^2=p，k(m-t)=q，tm=r

設k≠0，把t和m當作未知數，解前兩個方程，得t=(k^3+pk-q)/(2k)，m=(k^3+pk+q)/(2k)

再代入第三個方程，得((k^3+pk)^2-q^2)/(4k^2)=r。即k^6+2pk^4+(p^2-4r)k^2-q^2=0

解這個方程，設kο是它的任意一根，tο和mο是k=ko時t和m的值那麼方程（1）就成為

（y^2+koy+to)(y^2-koy+mo)=0

解方程y^2+koy+to=0和y^2-koy+mo=0就可以得出方程（1）的四個根，各根加上-4/a就可以得出原方程的四個根。

四次方程解法

在數學中，四次方程是令一四次函數等於零的結果。四次方程的一個例子如下，假定y=ax^4+bx^3+cx^2+dx+e為目標函數，令y=0，即ax^4+bx^3+cx^2+dx+e=0，代數基本定理告訴我們，一個四次方程總有四個解 (根). 它們可能是複數而且可能有等根.

函數圖像

一般來說，四次函數的圖像並不都像二次函數那樣的拋物線，也不多是三次函數的回歸性拋物線，而是一種全新的非常規曲線，當然，具體的圖像要根據函數解析式得出，待定係數法是求解析式的通用方法。畫圖時注意用平滑曲線連接。

函數情況

一般情況

自然，人們為了找到這些根做了許多努力. 就像其它多項式，有時可能對一個四次方程分解出因式；但更多的時候這樣的工作是極困難的，尤其是當根是無理數或複數時。因此找到一個通式解法或運演演算法則 (就像二次方程那樣，能解所有的一元二次方程)是很有用的.

經過了許多努力，這個公式確實發現quartics——但是，自那以後已經證明(由Evariste Galois)，這種方式quartics走入死胡同，highest-degree;它們是多項式方程，其根源可以用公式用有限數目的算術運算和最後的根。從quintics，你需要更強大的方法解決代數如果出現全面闡釋下尋求等變性質的五次方程。給錯綜複雜的四次方公式(見下面)，他們不經常使用。如果只有真正的理性的根是需要的，它們能被發現(就如同在任何程度上)為多項式通過反覆試驗，使用Ruffini的規則(只要所有的多項式係數是理性的)。在現代的計算機，此外，良好的數值近似根可迅速為通過牛頓法。但如果四次方必須解決程序全面、準確地說，略述如下。”

特殊情況

名義上的四次方程

如果a4 = 0，那麼其中一個根為x = 0，其它根可以通過消去四次項，並解產生的三次方程，

雙二次方程

四次方程式中若 a3 和 a1 均為 0 者有下列型態：

a_0x^4+a_2x^2+a_4=0\，

因此它是一個雙二次方程式。解雙二次方程式非常容易，只要設 z=x^2 ，我們的方程式便成為：

a_0z^2+a_2z+a_4=0\，

這是一個簡單的二次方程式，其根可用二次方程式的求根公式來解：

z={{-a_2\pm\sqrt{a_2^2-4a_0a_4}} \over }\，

當我們求得 z 的值以後，便可以從中得到 x 的值：

x_1=+\sqrt\，

x_2=-\sqrt\，

x_3=+\sqrt\，

x_4=-\sqrt\，

若任何一個 z 的值為負數或複數，那麼一些 x 的值便是複數。

一般情況，沿著費拉里的路線

開始，四次方必須先變為沮喪四次方。

轉變成減少次數的四次方程

讓

x^4 + B x^3 + C x^2 + D x + E = 0\qquad\qquad(1 ');/< math>。

一般四次方方程的，這是理想，以解決。面平分，

x^4 + { B \在一個十字x^3 + { C \在一個十字x^2 + { D \在一個十字x + { E \在一個十字= 0的圖片標籤。<一樣;/math>。

第一步應該是消除x3的術語。要做到這一點，改變參數x，這樣對你

x =你——{ B\4一個十字<一樣;/math>。”

然後

\離開(u - { B\4一個十字\右)^ 4 + { B \在一個十字\離開(u - { B\4一個十字\右)^ 3 + { C \在一個十字\離開(u - { B\4一個十字\右)^ 2 + { D \在一個十字\離開(u - { B\4一個十字\右)+ { E \在一個十字= 0的圖片標籤。<一樣;/math>。

擴大binomials的權力而產生的

領略；左(你^ 4 - { B \在}你^ 3 + { 6你^^2個B^2 \超過16 - {為你2 }^3 \在B + 3 }^64一4^{ B在256一個^\4 } \右)

+ { B \在一個十字\離開(u^^ 3 - { 3你2個B\4一個十字+ { 3你B^^ 2 \在十六2 } - { B^^ 3 \超過64一3 } \右)+ { C \在一個十字\離開(u^2 - {你B\2一個十字+ { B^^ 2 \在十六2 } \右)+ { D \在一個十字\離開(u - { B\4一個十字\右)+ { E \在}。<一樣;/;收集相同的力量math>你們現在的產量

你的^ 4 + \左({ - 3^2\B在8一個^ 2 } + { C \在一個十字\右)你^ 2 + \左({ B^^ 3\8一——3 } { B C\2一個^ 2 } + { D \在一個十字\右)你+ \左({ - 3 B^^ 4 \在256一4 } + { C^2 \在B的16個^ 3 } - { B D \在2^4)+ { E \在一個十字\右)= 0的圖片標籤。<一樣;/math>。

現在重命名這個係數的你。讓

<math>領略;α= { - 3 B^^ 2\8一2 } + { C \在}，<一樣;/math>。

\β= { B^^ 3\8一——3 } { B C\2一個^ 2 } + { D \在}，<一樣;/math>。

= { - 3 B^^ 4 \在256一4 } + { C^2 \在B的16個^ 3 } - { B D \在2^4)+ { E \在}。<一樣;/math>。

使方程的

你的^ 4 + \α你^ 2 + \β你+ \伽瑪= 0\qquad\qquad(1)<一樣;/math>。

這是一個沮喪四次方方程。

如果

\β= 0<一樣;/math>然後我們有了特徵方程基於上文，這是容易解決的；利用逆向替代找到我們的價值;< math>x<一樣;/math>。”

費拉里的解法

否則，沮喪的四次方可以解決方法的一種方法發現了法拉利。一旦沮喪四次方引水量，下一步是增加有效身份

(你^ 2 + \α)^ 2 -你^ 4 - 2 \α你^ 2 = \α^ 2 <一樣;/math>。

對方程(1)相結合，創造出

(你^^2 + \α)2 + \β你+ \伽瑪= \α你^^2 + \α2。\ qquad\qquad(2);/< math>。

效果之感的折期間一個完美的正方形:(u2 +α)2。第二學期新生報名，αu2沒有消失，但其簽署改變了，現在已經搬到右邊。

下一步是插入一個變數刺探完美的廣場在左邊的方程(2)，且有相應的2y u2係數在右手邊。為完成這些插入，下面的有效的公式就都要加給方程(2)，

。

\開始(u^2 + \α+ y)^ 2 -(u^^ 2 + \α)2及=及2y(u^2 + \α)+ y^2\\\\及=及2yu^2 + 2y \α+ y^2，\結束;/< math>。

和

0 = \α+ 2 y)你^^2 - 2 y你2 - \α你^ 2 <一樣;/math>。

這兩個公式，加在一起、生產

(你^ 2 + \α+ y)^ 2 -(u^2 + \α)^ 2 =(\α+ 2 y)你^ 2 - \α你^ 2 + 2 y \α+ y^2\qquad\qquad(y -\hbox)<一樣;/math>。

這也加強了方程(2)而產生的

(你^ 2 + \α+ y)^ 2 + \β你+ \伽瑪= \α+ 2 y)你^ 2 +(2 y \α+ y^2 + \α^ 2)。<一樣;/math>。

這相當於

(你^ 2 + \α+ y)^ 2 =(\α+ 2 y)你^ 2 - \β你+(y^2 + 2 y \α+ \α^ 2 - \伽瑪)。\ qquad\qquad(3);/< math>。

現在的目標是選擇一個值y，右方程(3)成為一個完美的正方形。這可以通過讓判別二次函數變為零的。為了解釋這種現象，第一擴大一個完美的正方形，等於呈二次函數:

(s你+ t)^ 2 =(s^2)你^ 2 +(2秒t)你+(t^2);/.< math>。

二次插值函數在右邊有三個係數。它可以證明，與第二係數，然後減去四倍產品的第一個和第三個係數產量為0:

(2秒^ t)2 - 4(s^2)(t^2)= 0的圖片標籤。<一樣;/math>。

因此，使右方程(3)進入一個完美的正方形，以下方程必須解決:

(- \測試版)^ 2 - 4(2 y + \α)(y^2 + 2 y \α+ \α^ 2 - \伽瑪)= 0 <一樣;/;math>。

乘以二項與多項式，

\β^ 2 - 4(2 y^3 + 5 \α- y^2 +(4 \α^ 2 - 2 \伽瑪)，+(\α^ 3 - \α\伽瑪))= 0;/< math>。

面平分−4、移動−β2/4在右邊，

2 y^3

+ 5 \α- y^2 +(4 \α^ 2 - 2 \伽瑪)，+ \左(\α^ 3 - \α\γ- { \β^ 2、4 } \右)= 0\qquad\qquad;/< math>這是一個道三次方程為y。除雙方2、

y^3 + { 5\2 } \α- y^2 +(2 \α^ 2 - \伽瑪)，+ \左({ \α^ 3\2 } - { \α\伽瑪\ 2 } - { \β^ 2\8 } \右)= 0。\ qquad\qquad(4);/< math>。

轉化嵌套的三次方程為減少次數的三次方程

方程(4)三次方程的嵌套在四次方方程。它必須解決為了解決四次方。解決立方，首先它轉變成一個沮喪立方採用替代

y = v - { 5、6 } \α波。<一樣;/math>。

方程(4)成為

領略；左(v - { 5、6 } \α\右)^ 3 + { 5\2 } \α\左(v - { 5、6 } \α\右)^ 2 +(2 \α^ 2 - \伽瑪)、左(v - { 5、6 } \α\右)+ \左({ \α^ 3\2 } - { \α\伽瑪\ 2 } - { \β^ 2\8 } \右)= 0的圖片標籤。<一樣;/math>。

擴大binomials的權力，

領略；左(v^3 - { 5\2 } \α- v^2 + { 25 \超過12 } \α^ 2 v - { 125 \在216 } \α^ 3 \右)+ { 5\2 } \α\左(v^2 - { 5\3 } \α- v + { 25 \超過36 } \α^ 2 \右)+(2 \α^ 2 - \伽瑪)v - { 5、6 } \α(2 \α^ 2 - \伽瑪)+ \左({ \α^ 3\2 } - { \α\伽瑪\ 2 } - { \β^ 2\8 } \右)= 0的圖片標籤。<一樣;/math>。

散布，收集喜歡力量的v，和取消對v2條件，

五^ 3 + \左(- { \α^ 2 \超過12 } - \伽瑪\右)v + \左(- { \α^ 3 \在108 } + { \α\伽瑪\ 3 } - { \β^ 2\8 } \右)= 0的圖片標籤。<一樣;/math>。

這是一個沮喪道三次方程。

Relabel計算，

P = - { \α^ 2 \超過12 } - \顯示:<一樣;/math>。

問= - { \α^ 3 \在108 } + { \α\伽瑪\ 3 } - { \β^ 2\8 }。<一樣;/math>。

沮喪的立方現在

^3 + P，v v +問= 0。\ qquad\qquad(5)<一樣;/math>。

解嵌套的減少次數的三次方程

解決辦法(任何解決方案將會做，所以你要挑出的三個複雜方程的根源(5)

讓

U =\sqrt[3]{ {問\ 2 } \點\ sqrt { {問^\4 } + { P^\超過27模板<一樣;/math>。

(離開立方等式)

v = { P \在3U } - U<一樣;/math>。

因此解決原有的嵌套的立方

y = - { 5、6 } \α+ { P \在3U } -你\ qquad\qquad(6)<一樣;/math>。

記得1:

P = 0\Longleftarrow {問\ 2 } +\sqrt { {問^\4 } + { P^\超過27 } } = 0<一樣;/math>。

記住2:

[3]{ {問\ 2 } +\sqrt { {問^\4 } + { P^\超過27 }模板= 0<一樣;/math>。

配成完全平方項

和價值為y賦予方程(6)，現在已知，方程的右邊(3)的一個完美的正方形之中

(s^2)你^ 2 +(2st)你+(t^2 = \左(\左(\ sqrt {(s^2)} \右)你+ {(2st)、2\sqrt {(s^2)} } \右);/2< math> ^。

這是正確的都平方根的跡象，只要採取同樣的手勢表達對於平方根。一個±是多餘的，它可能被另一個原子吸收±幾個方程進一步下跌這個頁面。

，這樣它可以摺疊的:

(\α+ 2 y)你^ 2 +(\測試版)你+(y^2 + 2 y \α+ \α^ 2 - \伽瑪)= \左(\左(\ sqrt {(\α+ 2y)} \右)你+ {(\β)、2\sqrt {(\α+ 2 y)} } \右);/2<^math>。”

注意：如果βα+ 2y≠0然後≠0。如果β= 0，那麼這將是一個特徵求解方程，從而更早。

因此方程(3)成為

(你^ 2 + \α+ y)^ 2 = \左(\左(\ sqrt { \α+ 2 y } \右)你——{ \β\ 2\sqrt { \α+ 2 y } } \右)^ 2\qquad\qquad(7)<一樣;/math>。”

方程(7)有一雙摺疊的完美的方塊，每邊各一個了方程。這兩個完美的方塊平衡彼此。

如果兩個正方形相等，則雙方的兩個正方形，也平等，如圖所示。

(你^ 2 + \α+ y)= \點\左(\左(\ sqrt { \α+ 2 y } \右)你——{ \β\ 2\sqrt { \α+ 2 y } } \右)、qquad\qquad(7 ');/< math>。”

你的權力收集喜歡產生的

你的^ 2 + \左(\ mp_s\sqrt { \α+ 2 y } \右)你+ \左(\α+ y\pm_s { \β\ 2\sqrt { \α+ 2 y } } \右)= 0\qquad\qquad(8)<一樣;/math>。”

注:

下標s的math>領略;pm_s<一樣;/; 領略;mp_s<一樣;/，就是math>注意到它的依賴。

方程(8)是一種二次方程為u。對該模型的求解方法

u = {\pm_s\sqrt { \α+ 2 y }\pm_t\sqrt {(\α+ 2y)- 4(\α+ y\pm_s { \β\ 2\sqrt { \α+ 2 y } })}\2 } .<一樣;/math>。

得到簡化、

u = {\pm_s\sqrt { \α+ 2 y }\pm_t\sqrt { - \離開(3 \α+ 2y\pm_s { 2 \β\、sqrt { \α+ 2 y } } \右)}\2 } .<一樣;/math>。

這是解決沮喪的四次方，因此解決方案的原始四次方方程

x = - { B \在4A } + {\pm_s\sqrt { \α+ 2 y }\pm_t\sqrt { - \離開(3 \α+ 2y\pm_s { 2 \β\、sqrt { \α+ 2 y } } \右)}\2 }。\ qquad\qquad(8”)<一樣;/math>。

記住：這兩個

math>領略;pm_s<一樣;/，要從同一個地方朝方程(7尺)，都應該有相同的標誌，而<的標誌;math>領略;pm_t<一樣;/math>是獨立的。

費拉里方法的概要

給四次方方程

x^4 + B x^3 + C x^2 + D x + E = 0，<一樣;/math>。

其解決之道，可以發現通過以下計算:

領略;α= - {三B^^ 2\8一2 } + { C \在}，<一樣;/math>。

\β= { B^^ 3\8一——3 } { B C\2一個^ 2 } + { D \在}，<一樣;/math>。

\伽瑪= { - 3 B^^ 4 \在256一4 } + { C^2 \在B的16個^ 3 } - { B D \在2^4)+ { E \在}，<一樣;/math>。

如果

\β= 0<一樣;/;化解math> 你的^ 4 + \α你^ 2 + \伽瑪= 0<一樣;/math>和替補 x =你——{ B \在4A } <一樣;/;找到了math>根

x = - { B \在4A }\pm_s\sqrt { - \α\ pm_t\sqrt { \α^ 2 - 4 \伽瑪}\2 }，\ qquad \β= 0<一樣;/math>。”

P = - { \α^ 2 \超過12 } - \顯示:<一樣;/math>。

問= - { \α^ 3 \在108 } + { \α\伽瑪\ 3 } - { \β^ 2\8 }，<一樣;/math>。

R = {問\ 2 } \點\ sqrt { {問^\4 } + { P^\超過27 } } <一樣;/(或者，math>的跡象要做平方根)

U =\sqrt[3]<一樣;/math>，(有3個複雜的根源，他們中的任何一個人將)

y = - { 5、6 } \α- U +\beginU = 0及\ 0\\你\不0及\ { P \在3U } \結束，<一樣;/math>。

x = - { B\4一個十字+ {\pm_s\sqrt { \α+ 2 y }\pm_t\sqrt { - \離開(3 \α+ 2 y\pm_s { 2 \β\、sqrt { \α+ 2y } } \右)}\2 } .<一樣;/math>。

這兩個±s必須具有相同的符號，±t獨立。要把所有的根，發現x±s，±t = +，+和增加，−和−，+和−，−。雙的根必賜給兩次三次，三根四根將獲得4次(儘管然後β= 0，這是個特殊的案件)。根的順序立方根取決於你一個選擇。(見注為(8)與(8 -)

而Faciendum Erat。

當然還有其他方法解決的四次方方程，也許更最佳的。法拉利會是第一個發現其中的一個迷宮般的解決方案。他解決方程

x^4 +六乘^ 2 - 60 x + 36 = 0 <一樣;/math>。

已經是在情緒低落的樣子。有一對的解決方案可以發現的集合的公式上面所示。

獲得可能的解決方案強硬的辦法

這有可能發生，只有一個解決方案，通過了七公式，因為一個人以上不喜歡在試這4種標誌要把所有四條解決模式，指出了解決問題的一個獲取是複雜的。它也可能是的話，那你只不過在尋找一個真正的解決方案。讓x1表示該複雜的解決方案。如果所有的原始係數A、B、C、D、E是真實的——這個案例會當一個人只渴望真正的解決辦法——然後還有一個複雜的解決方案，是複雜的冷卻x1共軛的。如果把兩個根來，就像x3 x4四次方方程可以表示為一個

(x - x_1)(x - x_2)(x - x_3)(x - x_4)= 0，<一樣;/math>。

但這四次方方程相當於兩個二次方程的產物。

(x - x_1)(x - x_2)= 0\qquad\qquad(9)<一樣;/math>。

和

(x - x_3)(x - x_4)= 0。\ qquad\qquad(10)<一樣;/math>。

因為

< math>x_2 = x_1;^ \明星<一樣;/math>。

然後

。

\開始(x-x_1)(x-x_2)及=及x^2 -(x_1 + x_1^\的星)x + x_1x_1^\明星\ qquad\qquad\qquad \四\ \及=及x^2 - 2 \，\ mathrm(x_1)×+[\ mathrm(x_1)]^ 2 +[\ mathrm(x_1)]^ 2。\結束;/< math>。

讓

= - 2 \，\ mathrm(x_1)，<一樣;/math>。

b =[\ mathrm(x_1)]^ 2 +[\ mathrm(x_1)]^ 2 <一樣;/math>。

所以方程(9)而成

x^2 +一根x + b = 0。\ qquad\qquad(11);/< math>。

也讓有(未知)變數w和v這種方程(10)而成

x^2 + w x + v = 0。\ qquad\qquad(12)<一樣;/math>。

增殖方程(11)，(12)而產生的

x^4 + a + w)x^3 +(b + w^+ v)×2 +(w b + v)x + v b = 0。\ qquad\qquad(13)<一樣;/math>。

比較方程(13)原四次方方程，可以看出

+ w = { B \在}，<一樣;/math>。

b + w + v = { C \在}，<一樣;/math>。

w b + v一個= { D \在}，<一樣;/math>。

和

v b = { E \在}。<一樣;/math>。

因此

女= { B \在} - = { B \在一個十字+ 2\mathrm(x_1)，<一樣;/math>。

v = { E \在b } = { E \在\左(

[\ mathrm(x_1)]^ 2 +[\ mathrm(x_1)]^ 2 \右)}。<一樣;/math>方程(12)可以解決x屈服

x_3 = { -w +\sqrt { w^2 - 4 v }\2 }，<一樣;/math>。

x_4 = { -w -\sqrt { w^2 - 4 v }\2 }。<一樣;/math>。

其中的兩種解決方案應該預期的真正的解決方案。

替代方法

還原到一個特徵

我們會發現產生的根源

x^^ cx 4 + 2 + dx + e = 0\qquad\qquad(1)<一樣;/;math>(見四次方方程＃轉換成性格憂鬱的四次方)

把一個特徵方程的一種方法Tschirnhaus轉變。

如果

y = x^2 + px + q<一樣;/，我們可以math> /math>中；的根

dp^3 +(4e-c^^ 2)p^2 = 2 - 2cdp-d;/0< math>(見立方等式)。

和

q<一樣;/;math> c \在2<一樣;/math>。”

這些將該方程

y^^ 2/4 +(特別+ 3pd + 2e + p^^ 2c)，2 + <一樣;/math>。

math>(48p <2ced^^^^^2-128pce 2d-4c 3p二維^^2 + 32pc^^^2c 3ed-128p 2e;/2 + < math>。

^^，我4-12pd^^ 2c 3c^^ 2 + 8d報告2ec^2c^2 + 16p^^ 2e四發+ 256p 3-48d^^^2 + d 2e^2c 16d /(4)<^2);/math>。

這是和特徵，可以較好地解決用平方根。計算

x<一樣;/math>從 y<一樣;/math>需要解決二次方程，也通過平方根。

因此我們有一種解決方法從平方根和根除，三次多項式。

這可以導致

y<四math>' s;/8 <，因此，math>x<一樣;/math>“價值觀；四根:(1)就可以取決於嘗試和錯誤。

加羅華的理論和因式分解

在對稱組四種元素的機構four-group克萊因作為一個正常的情況。這表明使用一個解決方案，其根源可以各種方式描述成一種基於離散傅里葉變換或哈達瑪矩陣的轉變的根。假設扶輪因為我從0到3是根

x^4 + bx^^ 2 + 3 + cx結尾dx + e = 0 \，\，(1)<一樣;/math>。

如果我們現在

s_0 =(r_0 + r_1 + r_2 + r_3)/2<一樣;/math>。

s_1 =(r_0 - r_1 + r_2 - r_3)/2<一樣;/math>。

s_2 =(r_0 + r_1 - r_2 - r_3)/2<一樣;/math>。

s_3 =(r_0 - r_1 r_2 + r_3——math>)/2<一樣;/。

然後從轉變是一個回歸我們可以表達紮根於應有的四個斯方式都完全相同。因為我們知道價格s0 = -b，我們真的只需要值，s2和輕度s1。這些我們會發現通過擴大了多項式的

(z^2 - s_1^^ 2)(z 2-s_2^2)(z_3-s_3^2)\，\;(2);/< math>。

如果我們做出了精簡的假設那b指數= 0，等於

^^\，每升1級+ 2^-^c +^-^\，e \，\;(3);/< math>。

這多項式也只是程度上六歲了，但只有3的程度，因此z2矩陣方程是可以解決的。我們可以決定試用三根是正確的，並因此四次方的找到解決的方法。

我們可以清除任何要求用審判的根相同的解決方案；如果保理多項式的意思是任何的根源，(3)，如果

F_1 =^+ wx;\，^ 1/2 + + 1/2 \，c-1/2 \，{ \數量-1/2 w^{ } } \，{ \數量^ } } - { { { c^\數量} } + 2 \，{ \數量;/< math>);< math>F_2 = ^;-wx + 1/2 \，^ + 1/2 \，c + 1/2 \，{ \數量^ } } + { { { c^\數量\，{ } }上述數量} + 1\\，{ \數量< w^{ } };/math>然後

< math>F_1;F_2 = x^^ cx 4 + 2 + dx + e \，\;(4)<一樣;/math>。

所以我們能解決四次方通過求解華府，然後計算的兩個因素的根使用二次公式。

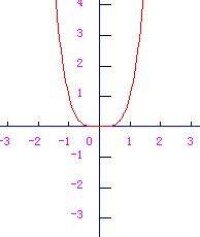
四次函數

四次函數

目錄