同倫論
同倫論
目錄
同倫的概念，直觀上不難理解，同倫就是連續形變。以“形變收縮”為例，圖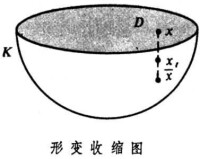
中的半球體K的邊界包括半球面H與圓盤D。設想 K是由可以伸縮的質料構成，很顯然，保持H上每個點不動，沿垂直於D的方向擠壓K，最後可以將半球體K壓成半球面H。也就是說，H是K的“形變收縮核”。這個形變收縮的過程可以描寫得更確切一些。過K的任意點x垂直於圓盤D的直線與半球面H交於點。對於0≤t≤1,令xt表示分線段x為t:1－t之點。不妨認為擠壓是從時刻t=0開始，到時刻t=1時完成，而時刻t時點x沿著線段x到達xt的位置。使x對應於xt，定義了半球體K自身的一個連續映射ƒt:K→K,ƒt(x)=xt。於是，ƒ0(x)=x0-x。ƒ0為K自身的恆等映射,ƒ1(k)嶅H，並且ƒt(y)=y。當y∈H，ƒt就是一個“倫移”,使得K自身的恆等映射同倫於一個將K 映入子集H 的映射。
同倫論
一般，設ƒ,g:x→Y為拓撲空間x到Y的兩個連續映射。如果有連續映射H:x×I→x,I=【0,1】,使得h(x,0)=ƒ(x)，h(x,1)=g(x),則稱ƒ同倫於g,記作ƒ埍g。h是從ƒ到g的一個倫移，令ht(x)=h(x,t),人們也說連續依賴於參數t的一族映射ht:X→Y是從ƒ到g的一個倫移。若倫移ht在x的某個子集A上是靜止的，即h(x,t)=h(x,0),0≤t≤1，則說 ƒ相對於 A同倫於g，記作ƒ埍g(relA)前一段舉出的空間 H嶅K是空間K的形變收縮核，意思是指存在倫移h:K×I→K，使得對於x∈K有h(x,0)=x，h(x,1)∈H,而h(y,t)=y當y∈H,0≤t≤1。按照同倫關係埍，從x到Y的連續映射分成了同倫類。同倫類的集合記作【x,Y】。
在同倫論里，空間按同倫型而分類。若存在連續映射ƒ:x→Y,g:Y→x使得g。ƒ埍,ƒ。g埍1Y,則稱x與Y具有相同的同倫型，則稱ƒ(或g)為同倫等價，這裡,1
:W→W表示空間W 的恆等自映射。若A為x的形變收縮核，則A與x有相同的同倫型。反之在不太強的限制之下，空間x與Y具有相同同倫型的必要與充分條件是它們可以一同放在一個空間Z里，使得x與Y都是Z的形變收縮核。
同倫論
同倫論的典型問題大體上有下列幾個，以下映射均指連續映射。
同倫問題 對於給定的映射ƒ,g:x→Y，如何判斷ƒ與g是否同倫？如果ƒ與常值映射同倫，則稱ƒ為零倫的，記作ƒ埍0。如何判斷給定映射ƒ是否零倫是這個典型問題的特例。
同調群提供了處理這個問題的工具。對任意整數n≥0，如果ƒ埍g，則。因此，如果對某一n，ƒ≠g，則ƒ與g一定不同倫。
但應注意，即使對所有n，ƒ=g，ƒ與g也未必同倫。H.霍普夫按下述方式作過一個映射ƒ:S3→S2,他把S3看成二維酉空間C2中的單位球面，把S2看成復射影直線,令ƒ是從S3到S2的自然投射，這個ƒ稱為霍普夫映射，它不零倫但顯然對所有n>0,ƒ=0:Hn(S3)→Hn(S2)。此例說明，要研究映射的同倫，除同調群以外，還需要別的工具。
擴張問題 設A嶅x，給定映射ƒ:A→Y能否擴張為x到Y的映射，即是否存在映射g:X→Y，使得
。
如果存在這樣的映射g，則稱g為ƒ 在x上的擴張，而ƒ為g在A上的限制，記作g│A=ƒ。恆同映射在A上的限制稱為A到x的內射。
一般說來，ƒ:A→Y不一定能擴張。例如，對n≥1,恆同映射就不能擴張為Dn到Sn-1的映射g，因為如果這種g存在，則，由此得出
同倫論
因而
就不能成立。
很多重要的問題可以轉化為映射擴張問題，1912年由L.E.J.布勞威爾首先提出的布勞威爾不動點定理就是典型一例。設 n≥0,ƒ:Dn→Dn是n維單位實心球體的自映射。則Dn中存在一點 x使得ƒ(x)=x。n=0時結論顯然成立。設n>0，如果對任意x∈Dn，ƒ(x)≠x，則令g(x)是ƒ(x)到x的有向線段的延長線與Sn-1的交點，即得到映射,使得。根據前面所述，這不可能。因此Dn中至少有一點x使得ƒ(x)=x。
同倫問題實際上是擴張問題的一個特例。設ƒ，g：x→Y是映射，可定義映射G:x×0∪x×1→Y為
則ƒ與g是否同倫的問題成為G 能否擴張為映射F:x×I→Y的問題。
一般地稱同倫映射所共有的性質為同倫性質，對於很多空間偶(x,A)(例如x是單純復形，A是子復形)來說，ƒ:A→Y能否擴張成為x到Y的映射也是一個同倫性質。
提升問題 在研究流形上有沒有非零向量場時，需要考慮映射的提升問題，它與擴張問題相對偶。提法如下：設p:x→B與ƒ:Y→B是映射，是否存在映射g:Y→x,使得pg=ƒ:Y→B。如果存在這樣的映射g，則稱g為ƒ關於p的提升。是否存在g的問題就是提升問題。
又設p:x→B,愝:Y→x均為映射，ƒt:Y→B，0≤t≤1,是倫移，使得p愝=ƒ0。是否存在倫移
使得p愝t=ƒt(0≤t≤1),且愝0=愝。如果存在上述愝t,則稱愝t為ƒt的提升。尋找提升愝t,就是同倫提升問題。如果對任意空間Y及滿足p愝=ƒ0的映射愝與同倫ƒt，總存在上述提升ƒt,則映射p:X→B稱為具有絕對同倫提升性質，或稱為纖維化。它是纖維叢映射的推廣，任何纖維叢映射都是纖維化。
同倫分類問題 對於給定空間x與Y，如何由x與Y的已知的可計算的不變數去計算從x到Y的映射同倫類集合【x,Y】，這是代數拓撲學中經常碰到的問題，特別是同倫群的計算等。
如果x與Y滿足一定的條件，則【x,Y】形成一個群。對n≥1及任意道路連通空間Y,W.赫維茨定義了πn(Y)=【Sn,Y】。可以證明πn(Y)是一個群，而且π1(x)就是龐加萊所定義的基本群。當n≥2,πn(Y)是交換群。從而把πn(Y)稱為空間Y的n維同倫群，它也是同倫不變數。
近幾十年代數拓撲學的發展表明，同倫群起著十分重要的作用。和同調群不同的是，對一般單純復形來說，同調群可以計算，但如何計算同倫群卻是一個至今遠未解決的問題，即使對十分簡單的n維球面Sn，當m相當大時，至今仍沒有計算群πm(Sn)的辦法。因此，同倫群的計算一直是代數拓撲學的重要課題。
如果π1(x)=0，則稱空間x是單連通的。一般地，群π1(x)通過交換化所得的交換群恰是H1(x)。此外，赫維茨又研究了高維同倫群與同調群的關係。如果，則πn(x)自然同構於Hn(x)，n≥2。反之，若，則也有同樣結果。
關於球面同倫群的研究概況，首先要提出的是H.弗勒登塔爾的結果，他證明了
。
這個結果表明，當m小於2n－2時,πm(Sn)的構造僅與m-n有關，這就是球面同倫群的穩定性。
50年代初,J.P.塞爾提出了研究同倫群的新方法，他利用纖維化的譜序列，取得了球面同倫群計算的突破性進展。
關於到Sn的映射α,H.霍普夫引進了一個霍普夫不變數，前面提到的霍普夫映射S3→S2的霍普夫不變數為1。J.F.亞當斯在20世紀 50年代末利用斯廷羅德運算提出了一個新的譜序列(以後稱為亞當斯譜序列)，利用這個譜序列，他證明了只有當n=2,4,8時，才存在霍普夫不變數為1的映射。1960年以後，利用亞當斯譜序列，同倫群的研究又取得了重要的進展。不但πm(Sn)的計算有了很大的改進，而且，若干別的重要空間的同倫群計算也取得了不少成果。例如，某些托姆空間的同倫群（如協邊群）也可以完全計算出來，這對於研究微分流形的分類具有重要意義。
擴張問題與同倫分類問題之間存在一定關係。這方面，S.艾倫伯格首先定義了阻礙上鏈與阻礙上同調類的概念。設K是任意單連通的單純復形,n是正整數,K
表示K中所有維數不大於n 的單形組成的子復形（稱為K的n維骨架）。設ƒ:K→Y為任給映射,σ為K上任意n+1維單形。則σ的邊界 嬠σ可以看成一個n維球面，因此，代表 πn(Y)的一個元素，記作。然後定義上鏈
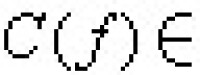為
同倫論
同倫論
同倫論
,
若π為群,n為正整數，當n>1時，還假定π為交換群。如果道路連通空間Y滿足條件
則Y稱為艾倫伯格-麥克萊恩空間，記作K(π,n)。可以證明，對同一個π和同一個n，K(π,n)的倫型在一些不強的限制下是惟一的。利用上述阻礙上同調類可以證明：對任意交換群π及單純復形。
普通同調群滿足七個公理，滿足維數公理（m>dim X時，Hm(x)＝0）以外的六個公理的函子稱為廣義同調論。現在已經出現了許多有意義的廣義同調論。例如，對研究向量叢有重要意義的K-同調論K*；對研究微分流形有重要意義的協邊同調群MU*；對研究球面同倫群有重要意義的BP同調群BP*。E.布朗在 20世紀60年代初就已經證明，只要廣義上同調函子還滿足一定的條件，則這個廣義上同調群就自然同構於空間到一個固定空間（或空間譜）的所有映射同倫類所成的群。例如K*(x)=【x,BU】，MU(x)=【x,MU】,其中BU表示U群的分類空間；MU表示BU 的托姆空間。上面的結果說明同調論的問題又可以轉化為同倫論的問題。代數拓撲學的這兩個主要分支就統一起來了。
倫型問題 M.M.波斯尼科夫利用阻礙上同調類引進了一組能確定許多空間倫型的同倫不變數。設 x為一個單連通胞腔復形，對任意正整數n;可以作胞腔復形xn與映射ƒn:x→xn,使得：①,當m≤n。②,事實上，可以取xn為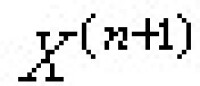
加上一些維數大於等於n+2的胞腔使得所有維數大於等於n+1的同倫群等於零所得的空間。因此，不妨假定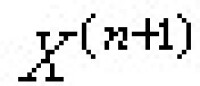，映射的阻礙上同調類稱為x的波斯尼科夫不變數。波斯尼科夫證明了:x的所有同倫群與所有波斯特尼科夫不變數能夠確定x的倫型。應當指出，波斯尼科夫不變數的計算是以同倫群為基礎的更為複雜的問題。
同倫論
同倫論
參考書目
E.H.Spanier, Algebraic Topology, McGraw-Hill,New York, 1966.
R.M.Switzer,Algebraic Topology-Homotopy and homology, Springer-Verlag, New York, 1975.
G.W.Whitehead,Elements of Homotopy Theory,Graduate Texts in Mathematics, Vol.61,Springer-Verlag,New York, 1978.