碰撞理論
碰撞理論
碰撞理論研究的是粒子間的一種相互作用。力學理論基礎是動量守恆定律和能量守恆定律。粒子多種多樣使碰撞理論分為：原子的碰撞、等離子體的碰撞等等。同屬於粒子間的相互作用的還有：輕原子核的聚合、正負電子的湮沒、荷電π介子的衰變、中子的beta衰變、核子N與π介子的相互作用、光子gamma與電子e的散射等。
物理學和化學之中都涉及到粒子間的相互作用。
每個物體的各自動能發生不連續變化的過程稱作物理碰撞，簡稱碰撞。例如，電子槍發射的高速電子與原子核外電子之間的相互作用。其中，軔致輻射應該是沒有發生碰撞的，所以動能變化是連續的。而且，如果電子在原子核外電子電場力的作用下減速后，還具有充足的動能，就會把原子的內層電子碰撞出軌道。碰撞過程的每個電子的各自動能的變化是不連續的。
有新物質生成的過程稱為化學反應，簡稱反應。例如，輕原子核（含氫H的同位素）的聚合生成氦He、質子p和中子n。
物理化學研究的是二者兼有的相互作用。
並非每一次碰撞都發生預期的反應,只有非常少非常少的碰撞是有效的。首先,分子無限接近時,要克服斥力,這就要求分子具有足夠的運動速度,即能量.具備足夠的能量是有效碰撞的必要條件.一組碰撞的反應物的分子的總能量必須具備一個最低的能量值,這種能量分佈符合從前所講的分佈原則.用E表示這種能量限制,則具備E和E以上的分子組的分數為:
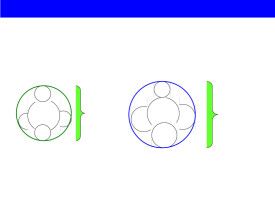
其次,僅具有足夠能量尚不充分,分子有構型,所以碰撞方向還會有所不同,如反應:
的碰撞方式有:
（a）
（b）
顯然,(a)種碰接有利於反應的進行,(b)種以及許多其它碰撞方式都是無效的.取向適合的次數佔總碰撞次數的分數用p表示.
若單位時間內,單位體積中碰撞的總次數為Z mol,則反應速率可表示為:
, 其中 p 稱為取向因子, f 稱為能量因子.或寫成:
將具備足夠能量(碰撞後足以反應)的反應物分子組,稱為活化分子組.
Ea越大,活化分子組數則越少,有效碰撞分數越小,故反應速率越慢.
不同類型的反應,活化能差別很大.如何反應:
而中和反應：
分子不斷碰撞,能量不斷轉移,因此,分子的能量不斷變化,故活化分子組也不是固定不變的.但只要溫度一定,活化分子組的百分數是固定的.
粒子分裂
利用動量守恆和能量守恆定律可以得到一系列關於各種力學過程特性的結論。特別重要的是，這些性質完全不依賴於粒子間具體的相互作用形式。
粒子分裂研究的是粒子自動、沒有外力作用分裂成兩個組成部分的問題，分裂后兩個粒子獨立運動。
在粒子分裂前靜止的參考系中觀察這個過程是最簡單的。根據動量守恆定律，分裂后兩個粒子動量之和仍為零，即兩個粒子的動量大小相等方向相反。動量的大小可以由能量守恆定律：
確定，其中和是兩個粒子的質量，和是兩個粒子的內能，而是原來粒子的初始內能。用表示分裂能，即：
能量為正時反應才可能發生。由此可以確定動量的大小，兩個粒子的速度分別為：
如果兩個粒子碰撞不改變兩個粒子的內部狀態，那麼稱為彈性碰撞。研究彈性碰撞應用能量守恆定律時不必考慮內能。
根據動量守恆定律，碰撞前後兩個粒子動量矢量不變；又，根據能量守恆定律，碰撞前後兩個粒子能能量不變設碰碰撞個粒子的速度為和，那麼碰撞后兩個粒子的速度與其的關係可由兩個定律推導得到：其中是矢量。
粒子散射
在物理應用中經常遇到的是，以相同速度飛向散射中心的粒子束的散射。不同的粒子有不同的瞄準距離，因此以不同的角度散射。
設有一束實驗粒子，相對於靶心的速度為，粒子數密度為，定義粒子流強，表示單位時間內，通過垂直於粒子流方向的單位面積的粒子數。選取球坐標系，設極軸（z軸）與入射粒子運動方向一致，靶粒子位於坐標原點。單位時間內，流強為的粒子流被一個類粒子散射后，通過立體角元的類粒子數正比於流強和立體角元：
其中，是單位時間內通過立體角元的粒子數。稱為微分散射截面，但其實是一個比例係數。這裡的和都是泛指粒子的類型，而不是特指粒子和粒子。這是因為這個比例係數是和實驗粒子、散射中心粒子的類型有關的。
微分散射截面，是如果未發生散射時粒子束所通過的平面的面元，與發生散射時粒子束所通過的立體角元所在球面的面元，二者面積的比值。
單位面積與微分
如果不考慮完全反彈粒子，那麼微分散射截面在散射中心粒子身上，只取決於這個粒子的上面一小部分，和下面一小部分。
是單位時間內通過平面單位面積的粒子數。與的乘積，就是單位時間內通過球面單位面積的粒子數。
速度速度單位時間內穿過的距離。在勻速運運動的前提動的前提距離和單位時間一定是一致的，因此，這段單位距離，就指的是到屏上立體角元的距離。
是立體角元。
“單位面積”不同於“微分”。平面和球面的單位面積一定是相同的，但是微分可以不同。
根據立體角元微分：
因為所求的是立體角元通過的粒子數，而立體角元是對球面有意義的，因此應該認為是單位面積，那麼一定比單位面積小，而且一定等於單位面積的倍。
因此，通過球面單位面積的粒子數，一定就等於通過平面單位面積的粒子數的倍。這個比值就稱為“微分散射截面”。
歷史上第一個核反應，是盧瑟福於1919年觀察到的。盧瑟福利用釙的同位素放出的能量為7.68的粒子撞擊氮氣時發現了如下反應：
粒子表示氦原子，表示質子。
等離子體是由大量做自由運動的和相互作用（碰撞）的帶電粒子所組成的系統。在這個系統中，碰撞對等離子體宏觀特性的影響是對大量碰撞過程的平均的結果。
庫侖碰撞是等離子體中帶電粒子之間的碰撞，與一般二體碰撞具有顯著的不同。
碰撞理論
另一方面，散射中心對德拜球內的所有帶電粒子同時發生相互作用，因此，等離子體中帶電粒子的相互作用一般是多體相互作用，而不像中性粒子之間的碰撞是二體。當然，當碰撞參數很小時，所觀察的兩個帶電粒子的相互作用，可以近似地忽略其他帶電粒子存在的影響，近似地看成二體碰撞。對於一般多體碰撞，在一定近似下，也可以看成一系列無關的二體碰撞的疊加。
在什麼條件下，才能夠實現狄拉克理論所預言的電子-正電子對呢？正能態能級和負能態能級之間存在著的間距。為了產生電子對，必須讓真空吸收能量大於的光子，這樣，“負能電子海”中一個電子激發越過禁區，跳到正能態能級區，表現為一個正能量的電子，同時留下的電子“空穴”則表現為一個帶正電荷的正電子。綜合上述，發生了如下的過程：
條件是“原子核場中”。
反過來講，如果電子海中有一個空位（即有一個正電子），那麼正能態電子（即電子），就能夠跳到這個空位上去，並放出能量和大於的光子。伴隨著光子的產生，電子對消失了。正負電子相遇，可以轉變為兩個光子，記作。
這個過程叫做正負電子對的湮沒過程，或簡稱正電子湮沒。
兩個輕原子核聚合成一個中等質量原子核的現象稱為原子核的聚變。
括弧中的數字代表粒子攜帶的能量。這四個反應的總結果可以看做是6個氘核聚合成兩個並放出兩個質子和兩個中子，同時釋放出能量的過程，即
平均每個核子釋放的能量是，大約是中子誘發鈾的同位素裂變時每個核子所釋放能量的倍。
粒子的相互作用包括：
（1）衰變
（2）中子衰變
上面有一條橫線。
（3）彈性散射
（4）散射
基本信息
- 中文名
- 碰撞理論
- 外文名
- collision threory
- 研究範圍
- 研究的是粒子間的一種相互作用
- 應用學科
- 物理學（化學、物理化學）