橢圓函數
雙周期的亞純函數
目錄
一個函數ƒ(z),如果存在著常數T≠0(可以是複數),使對一切z均有
ƒ(z+T)=ƒ(z) (1)
則稱ƒ(z)為周期函數,T為其周期。可使周期T滿足式(1)且有最小的模。
如果一函數ƒ(z)有兩個周期2ω,2ω┡,且(以下恆設其>0),則稱ƒ(z)為雙周期函數。一般說來,ƒ(z)在z=z0附近的性態與在附近的性態相同,m,n為任何整數;z0+稱作z0的(周期)合同點。因此,研究ƒ(z)例如可只限於z在以0,2ω1=2ω,2ω2=2(ω+ω┡),2ω3=2ω┡為頂點的平行四邊形p中變動。這個平行四邊形稱為ƒ(z)的基本周期四邊形或基本胞腔(見圖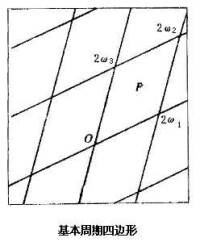 )。
)。

橢圓函數
只有極點的雙周期解析函數ƒ(z)就是橢圓函數。不妨假設在p的周界上沒有ƒ(z)的零點和極點,因為否則只要對復坐標z作適當平移變換便可達到目的。
由劉維爾定理知,雙周期解析函數ƒ(z)如果沒有奇點則必為常數。又由留數定理易證,ƒ(z)在p 中也不可能只有一個單極點。且可證明,ƒ(z)在p 中取任何值的點的個數包括極點的個數(重數也計入個數內)均相同。橢圓函數在p中極點的個數稱作它的階數。因此,(非常數的)橢圓函數至少是二階的。
ξ函數與P函數 定義
(2)
式中∑┡表示對一切整數m,n求和,但m=n=0除外。ξ(z)是一亞純函數,以為單極點(m,n=0,±1,±2,…),且主部為。它不是周期函數,但滿足下列關係:
(3)
式中ηj=ξ(ωj)為三個常數,它們之間有如下關係:
由式(3)可見
已是一個二階橢圓函數,以為二階極點,並以為其主部。
任何橢圓函數均可通過 P(z)及其各階導函數表出。
函數P(z)滿足微分方程
式中。P函數還有所謂加法公式
σ函數 為了得到橢圓函數的一種方便的表示法,引進σ函數。
,
式中∏┡表示對一切整數m,n求積,但m=n=0除外。σ(z)是以為單零點的整函數,它不是雙周期的,但滿足下列關係:
橢圓函數
任何n階橢圓函數ƒ(z),如分別以α1,α2,…,αn和β1,β2,…,βn為其零點和極點(計入重數),則總可使得,這時它可表為
式中C為一常數。如記
,
則可證
式中,且根式已適當選定一支。
θ函數 在實際應用中,作變換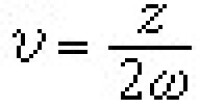 ,可使橢圓函數ƒ(z)變成另一橢圓函數φ(υ),後者的一個周期為1,另一周期為。引進θ函數
,可使橢圓函數ƒ(z)變成另一橢圓函數φ(υ),後者的一個周期為1,另一周期為。引進θ函數
橢圓函數
式中q=。θ(υ)不是橢圓函數,但有
由θ(υ)還可引進 函數如下:
函數如下:
橢圓函數
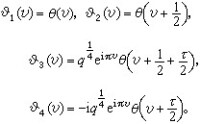
橢圓函數
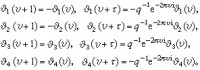
橢圓函數
如前式中αr,βr(r=1,…,n)為ƒ(z)的零點與極點。
P(z)與 k(υ)間有如下確定的關係:
k(υ)間有如下確定的關係:
橢圓函數
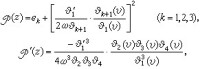
橢圓函數
橢圓函數
雅可比橢圓函數令(根號取定一值),定義雅可比橢圓函數如下:
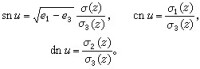
橢圓函數
,
等等。由這些公式,可得
橢圓函數
這裡根式應選取u=0時取值 +1的一支,由此可以得出

橢圓函數
右邊這類含有四次根式的積分正是求橢圓的弧長時會遇到的那種類型,它們統稱為橢圓積分。由式(4)可見,u作為z的函數時,其反函數正好是橢圓函數snu。橢圓函數名稱來源於此。
自守函數 橢圓函數ƒ(z)具有這樣一個特點:當z經過平移變換
后函數值不變。變換T,T┡生成一群G,ƒ(z)的變數z經G中任何變換后ƒ(z)保持不變。
一般說來,設G ={T}為分式線性變換構成的群(但不是單位群,即不是由恆等變換一個元構成的群),又設ƒ(z)為某區域D中的亞純函數,群G中的任何元T把D變成自身。且使
,
則稱ƒ(z)為區域D中關於群G的自守函數。橢圓函數就是全平面中關於群整數}的自守函數。