母函數
母函數
生成函數即母函數,是組合數學中尤其是計數方面的一個重要理論和工具。
生成函數有普通型生成函數和指數型生成函數兩種,其中普通型用的比較多。形式上說,普通型生成函數用於解決多重集的組合問題,而指數型母函數用於解決多重集的排列問題。[請大牛補充解釋]
最早提出母函數的人是法國數學家LaplaceP.S.在其1812年出版的《概率的分析理論》中明確提出“生成函數的計算”,書中對生成函數思想奠基人——Euler L在18世紀對自然數的分解與合成的研究做了延伸與發展。生成函數的理論由此基本建立。
生成函數的應用簡單來說在於研究未知(通項)數列規律,用這種方法在給出遞推式的情況下求出數列的通項,生成函數是推導Fibonacci數列的通項公式方法之一,另外組合數學中的Catalan數也可以通過生成函數的方法得到。
定義:
對於任意數列a0,a1,a2...an 即用如下方法與一個函數聯繫起來:
~G(x) = a0 + a1x + a2x*2 + a3x^3 +....+ anx^n
則稱G(x)是數列的生成函數(generating function)
例子:
比較典型的是:A(x) = (1+x)^n~C(n,0),C(n,1),C(n,2),C(n,3),.....,C(n,n)
基本運算:
 用圖片表示
用圖片表示生成函數是說,構造這麼一個多項式函數g(x),使得x的n次方係數為f(n)。如:序列{0,1,2,3,4,5...n}的生成函數為:f(x)=0+x+2x^2+3x^3+4x^4+...+nx^n
生成函數最絕妙的是,某些生成函數可以化簡為一個很簡單的函數。也就是說,不一定每個生成函數都是用一長串多項式來表示的。比如,這個函數f(n)=1 (n當然是屬於自然數的),它的生成函數就應該是g(x)=1+x+x^2+x^3+x^4+...(每一項都是一,即使n=0時也有x^0係數為1,所以有常數項)。再仔細一看,這就是一個有無窮多項的等比數列求和嘛。如果-1
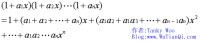 由此可以看出:
由此可以看出: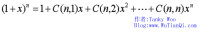 母函數的定義:
母函數的定義: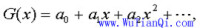 圖三
圖三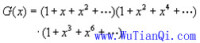 以展開后的x為例,其係數為4,即4拆分成1、2、3之和的拆分數為4;
以展開后的x為例,其係數為4,即4拆分成1、2、3之和的拆分數為4;
我們舉一個例子說明,一些具有實際意義的組合問題也可以用像這樣簡單的一個函數全部表示出來。
考慮這個問題:從二班選n個MM出來有多少種選法。學過簡單的排列與組合的同學都知道,答案就是C(4,n)。也就是說。從n=0開始,問題的答案分別是1,4,6,4,1,0,0,0,...(從4個MM中選出4個以上的人來方案數當然為0嘍)。那麼它的生成函數g(x)就應該是g(x)=1+4x+6x^2+4x^3+x^4。這不就是……二項式展開嗎?於是,g(x)=(1+x)^4。
你或許應該知道,(1+x)^k=C(k,0)x^0+C(k,1)x^1+...+C(k,k)x^k;但你或許不知道,即使k為負數和小數的時候,也有類似的結論:(1+x)^k=C(k,0)x^0+C(k,1)x^1+...+C(k,k)x^k+C(k,k+1)x^(k+1)+C(k,k+2)x^(k+2)+...(一直加到無窮;式子看著很彆扭,自己寫到草稿紙上吧,畢竟這裡輸入數學式子很麻煩)。其中,廣義的組合數C(k,i)就等於k(k-1)(k-2)(k-i+1)/i!,比如C(4,6)=4*3*2*1*0*(-1)/6!=0,再比如C(-1.4,2)=(-1.4)*(-2.4)/2!=1.68。後面這個就叫做牛頓二項式定理。當k為整數時,所有i>k時的C(k,i)中分子都要“越過”0這一項,因此後面C(k,k+1),C(k,k+2)之類的都為0了,與我們的經典二項式定理結論相同;不同的是,牛頓二項式定理中的指數k可以是任意實數。
我們再舉一個例子說明一些更複雜的生成函數。n=x1+x2+x3+...+xk有多少個非負整數解?這道題是學排列與組合的經典例題了。把每組解的每個數都加1,就變成n+k=x1+x2+x3+...+xk的正整數解的個數了。教材上或許會出現這麼一個難聽的名字叫“隔板法”:把n+k個東西排成一排,在n+k-1個空格中插入k-1個“隔板”。答案我們總是知道的,就是C(n+k-1,k-1)。它就等於C(n+k-1,n)。它關於n的生成函數是g(x)=1/(1-x)^k。這個生成函數是怎麼來的呢?其實,它就是(1-x)的-k次方。把(1-x)^(-k)按照剛才的牛頓二項式展開,我們就得到了x^n的係數恰好是C(n+k-1,n),因為C(-k,n)*(-x)^n=[(-1)^n*C(n+k-1,n)]*[(-1)^n*x^n]=C(n+k-1,n)x^n。這裡看暈了不要緊,後文有另一種方法可以推導出一模一樣的公式。事實上,我們有一個純組合數學的更簡單的解釋方法。因為我們剛才的幾何級數1+x+x^2+x^3+x^4+...=1/(1-x),那麼(1+x+x^2+x^3+x^4+...)^k就等於1/(1-x)^k。仔細想想k個(1+x+x^2+x^3+x^4+...)相乘是什麼意思。(1+x+x^2+x^3+x^4+...)^k的展開式中,n次項的係數就是我們的答案,因為它的這個係數是由原式完全展開后k個指數加起來恰好等於n的項合併起來得到的。
現在我們引用《組合數學》上暴經典的一個例題。很多書上都會有這類題。
結合剛才的k個(1+x+x^2+x^3+x^4+...)相乘,我們也可以算出這個問題的生成函數。
引用內容
g(x)=(1+x^2+x^4+...)(1+x^5+x^10+..)(1+x+x^2+x^3+x^4)(1+x)
=[1/(1-x^2)]*[1/(1-x^5)]*[(1-x^5)/(1-x)]*(1+x) (前兩個分別是公比為2和5的幾何級數,
第三個嘛,(1+x+x^2+x^3+x^4)*(1-x)不就是1-x^5了嗎)
=1/(1-x)^2 (約分,把一大半都約掉了)
=(1-x)^(-2)=C(1,0)+C(2,1)x+C(3,2)x^2+C(4,3)x^3... (參見剛才對1/(1-x)^k的展開)
=1+2x+3x^2+4x^3+5x^4+....
於是,拿n個水果有n+1種方法。我們利用生成函數,完全使用代數手段得到了答案!
如果你對1/(1-x)^k的展開還不熟悉,我們這裡再介紹一個更加簡單和精妙的手段來解釋1/(1-x)^2=1+2x+3x^2+4x^3+5x^4+....。
1/(1-x)=1+x+x^2+x^3+x^4+...是前面說過的。我們對這個式子等號兩邊同時求導數。於是,1/(1-x)^2=1+2x+3x^2+4x^3+5x^4+....。一步就得到了我們所需要的東西!不斷地再求導數,我們同樣可以得到剛才用複雜的牛頓二項式定理得到的那個結論。生成函數還有很多其它的處理手段,比如等式兩邊同時乘以、除以常數(相當於等式右邊每一項乘以、除以常數),等式兩邊同時乘以、除以一個x(相當於等式右邊的係數“移一位”),以及求微分積分等。神奇的生成函數啊。
我們用兩種方法得到了這樣一個公式:1/(1-x)^n=1+C(n,1)x^1+C(n+1,2)x^2+C(n+2,3)x^3+...+C(n+k-1,k)x^k+...。這個公式非常有用,是把一個生成函數還原為數列的武器。而且還是核武器。
接下來我們要演示如何使用生成函數求出Fibonacci數列的通項公式。
Fibonacci數列是這樣一個遞推數列:f(n)=f(n-1)+f(n-2)。現在我們需要求出它的生成函數g(x)。g(x)應該是一個這樣的函數:
g(x)=x+x^2+2x^3+3x^4+5x^5+8x^6+13x^7+...
等式兩邊同時乘以x,我們得到:
x*g(x)=x^2+x^3+2x^4+3x^5+5x^6+8x^7+...
就像我們前面說過的一樣,這相當於等式右邊的所有係數向右移動了一位。
現在我們把前面的式子和後面的式子相加,我們得到:
g(x)+x*g(x)=x+2x^2+3x^3+5x^4+8x^5+...
把這最後一個式子和第一個式子好好對比一下。如果第一個式子的係數往左邊移動一位,然後把多餘的“1”去掉,就變成了最後一個式子了。由於遞推函數的性質,我們神奇地得到了:g(x)+x*g(x)=g(x)/x-1。也就是說,g(x)*x^2+g(x)*x-g(x)=-x。把左邊的g(x)提出來,我們有:g(x)(x^2+x-1)=-x。於是,我們得到了g(x)=x/(1-x-x^2)。
現在的任務是要把x/(1-x-x^2)還原成通項公式。這不是我們剛才的1/(1-x)^n的形式,我們要把它變成這種形式。我們發現,1-x-x^2=[1-(1-√5)x/2]*[1-(1+√5)x/2] ((1-√5)/2和(1+√5)/2是怎麼算出來的?顯然它們應該是x^2-x-1=0的兩個根)。那麼x/(1-x-x^2)一定能表示成?/[1-(1-√5)x/2]+?/[1-(1+√5)x/2]的形式(再次抱歉,輸入數學公式很麻煩,將就看吧)。這是一定可以的,因為適當的?的取值可以讓兩個分式通分以後分子加起來恰好為一個x。?取值應該是多少呢?假設前面一個?是c1,後面那個是c2,那麼通分以後分子為c1*[1-(1+√5)x/2]+c2*[1-(1-√5)x/2],它恰好等於x。我們得到這樣兩個式子:常數項c1+c2=0,以及一次項-c1*(1+√5)/2-c2*(1-√5)/2=1。這兩個式子足夠我們解出c1和c2的準確值。你就不用解了,我用的Mathematica 5.0。解出來c1=-1/√5,c2=1/√5。你不信的話你去解吧。現在,我們把x/(1-x-x^2)變成了-(1/√5)/[1-(1-√5)x/2] + (1/√5)/[1-(1+√5)x/2]。我們已經知道了1/[1-(1-√5)x/2]的背後是以(1-√5)/2為公比的等比數列,1/[1-(1+√5)x/2]所表示的數列公比為(1+√5)/2。那麼,各乘以一個常數,再相加,我們就得到了Fibonacci數列的通項公式:f(n)=-(1/√5)*[(1-√5)/2]^n + (1/√5)*[(1+√5)/2]^n。或許你會問,這麼複雜的式子啊,還有根號,Fibonacci數列不都是整數嗎?神奇的是,這個充滿根號的式子對於任何一個自然數n得到的都是整數。熟悉用特徵方程解線性遞推方程的同學應該知道,以上過程實質上和找特徵根求解沒有區別。事實上,用上面所說的方法,我們可以求出任何一個線性齊次遞推方程的通項公式。什麼叫做線性齊次遞推呢?就是這樣的遞推方程:f(n)等於多少個f(n-1)加上多少個f(n-2)加上多少個f(n-3)等等。Fibonacci數列的遞推關係就是線性齊次遞推關係。
我們最後看一個例子。我們介紹硬幣兌換問題:我有1分、2分和5分面值的硬幣。請問湊出n分錢有多少種方法。想一下剛才的水果,我們不難得到這個問題的生成函數:g(x)=(1+x+x^2+x^3+...)(1+x^2+x^4+...)(1+x^5+x^10+..)=1/[(1-x)(1-x^2)(1-x^5)]。現在,我們需要把它變成通項公式。我們的步驟同剛才的步驟完全相同。我們把(1-x)(1-x^2)(1-x^5)展開,得到1-x-x^2+x^3-x^5+x^6+x^7-x^8。我們求出-1+x+x^2-x^3+x^5-x^6-x^7+x^8=0的解,得到了以下8個解:-1,1,1,1,-(-1)^(1/5),(-1)^(2/5),-(-1)^(3/5),(-1)^(4/5)。這個不是我解出來的,我還是用的Mathematica 5.0。不是我不想解,而是我根本不會解這個8次方程。這也是為什麼信息學會涉及這些東西的原因:次數稍微一高,只好交給計算機解決了。於是,(1-x)(1-x^2)(1-x^5)=(1+x)(1-x)^3(1+(-1)^(1/5) x)()()() (省略不寫了)。注意那個(1-x)^3。由於等根的出現,我們不得不把(1-x)^3所包含的(1-x)和(1-x)^2因子寫進一會兒的分母里,不然會導致解不出合適的c來。你可以看到很多虛數。不過沒關係,這些虛數同樣參與運算,就像剛才的根式一樣不會影響到最後結果的有理性。然後,我們像剛才一樣求出常數滿足1/(1-x)(1-x^2)(1-x^5)=c1/()+c2/(1-x)+c3/(1-x)^2+c4/(1-x)^3...+c8/()。這個解太複雜了,我用Mathematica解了幾分鐘,列印出了起碼幾十KB的式子。雖然複雜,但我確實是得到了通項公式。你有興趣的話可以嘗試用Mathematica解決一下1/[(1-x)(1-x^3)] (只有1分和3分的硬幣)。解c的值時可以用SolveAlways[]函數。你可以親眼見到,一個四五行的充滿虛數的式子最後總是得到正確的整數答案。
生成函數還有很多東西,例如:Catalan數列啊,指數生成函數啊,之類的。
在數學中,某個序列的母函數是一種形式冪級數,其每一項的係數可以提供關於這個序列的信息。使用母函數解決問題的方法稱為母函數方法。
母函數可分為很多種,包括普通母函數、指數母函數、L級數、貝爾級數和狄利克雷級數。對每個序列都可以寫出以上每個類型的一個母函數。構造母函數的目的一般是為了解決某個特定的問題,因此選用何種母函數視乎序列本身的特性和問題的類型。
這裡先給出兩句話,不懂的可以等看完這篇文章再回過頭來看:“把組合問題的加法法則和冪級數的t的乘冪的相加對應起來”
“母函數的思想很簡單—就是把離散數列和冪級數一一對應起來,把離散數列間的相互結合關係對應成為冪級數間的運算關係,最後由冪級數形式來確定離散數列的構造. “
我們首先來看下這個多項式乘法: (以下圖片都可以點擊放大)
母函數詳解
1.x的係數是a1,a2,…an 的單個組合的全體。
2. x2的係數是a1,a2,…a2的兩個組合的全體。
………
n. xn的係數是a1,a2,….an的n個組合的全體(只有1個)。
由此得到:如有圖
母函數詳解
對於序列a0,a1,a2,…構造一函數:
母函數詳解
稱函數G(x)是序列a0,a1,a2,…的母函數
這裡先給出2個例子,等會再結合題目分析:第一種:
有1克、2克、3克、4克的砝碼各一 枚,能稱出哪幾種重量?每種重量各有幾種可能方案?
考慮用母函數來解決這個問題:
我們假設x表示砝碼,x的指數表示砝碼的重量,這樣:
1個1克的砝碼可以用函數1+x表示,
1個2克的砝碼可以用函數1+x∧2表示,
1個3克的砝碼可以用函數1+x∧3表示,
1個4克的砝碼可以用函數1+x∧4表示,
上面這四個式子懂嗎?
我們拿1+x來說,前面已經說過,x表示砝碼,x的指數表示砝碼的重量!即這裡就是一個質量為2的砝碼,那麼前面的1表示什麼?按照上面的理解,1其實應該寫為:1*x^0,即1代表重量為2的砝碼數量為0個。(理解!)
不知道大家理解沒,我們這裡結合前面那句話:
“把組合問題的加法法則和冪級數的t的乘冪的相加對應起來“
1+x表示了兩種情況:1表示質量為2的砝碼取0個的情況,x表示質量為2的砝碼取1個的情況。這裡說下各項係數的意義:
在x前面的係數a表示相應質量的砝碼取a個,而1就表示相應砝碼取0個,這裡可不能簡單的認為相應砝碼取0個就該是0*x(想下為何?結合數學式子)。
所以,前面說的那句話的意義大家可以理解了吧?幾種砝碼的組合可以稱重的情況,可以用以上幾個函數的乘積表示:
(1+x)(1+x∧2)(1+x∧3)(1+x∧4)
= (1+x+x^2+x^3)(1+x^3+x^4+x^7)
=1+x+x^2+2x^3+2x^4+2x^5+2x^6+2x^7+x^8+x^9+x^10
從上面的函數知道:可稱出從1克到10克,係數便是方案數。(!!!經典!!!)
例如右端有2x項,即稱出5克的方案有2:5=3+2=4+1;同樣,6=1+2+3=4+2;10=1+2+3+4。
故稱出6克的方案有2,稱出10克的方案有1 。
接著上面,接下來是第二種情況:求用1分、2分、3分的郵票貼出不同數值的方案數:
大家把這種情況和第一種比較有何區別?第一種每種是一個,而這裡每種是無限的。
母函數詳解
即:4=1+1+1+1=1+1+2=1+3=2+2
這裡再引出兩個概念整數拆分和拆分數:
所謂整數拆分即把整數分解成若干整數的和(相當於把n個無區別的球放到n個無標誌的盒子,盒子允許空,也允許放多於一個球)。
整數拆分成若干整數的和,辦法不一,不同拆分法的總數叫做拆分數。
現在以上面的第二種情況每種種類個數無限為例,給出模板:
// Author: Tanky Woo
// 母函數詳解
using namespace std;
const int _max = 10001;
// c1是保存各項質量砝碼可以組合的數目
// c2是中間量,保存每一次的情況
int c1[_max], c2[_max];
int main()
{ //int n,i,j,k;
int nNum; //
int i, j, k;
while(cin >> nNum)
{
for(i=0; i<=nNum; ++i) // ---- ①
{
c1[i] = 1;
c2[i] = 0;
}
for(i=2; i<=nNum; ++i) // ----- ②
{
for(j=0; j<=nNum; ++j) // ----- ③
for(k=0; k+j<=nNum; k+=i) // ---- ④
{
c2[j+k] += c1[j];
}
for(j=0; j<=nNum; ++j) // ---- ⑤
{
c1[j] = c2[j];
c2[j] = 0;
}
}
cout << c1[nNum] << endl;
}
return 0;
}
我們來解釋下上面標誌的各個地方:(***********!!!重點!!!***********)
① 、首先對c1初始化,由第一個表達式(1+x+x+..x)初始化,把質量從0到n的所有砝碼都初始化為1.
② 、 i從2到n遍歷,這裡i就是指第i個表達式,上面給出的第二種母函數關係式里,每一個括弧括起來的就是一個表達式。
③、j 從0到n遍歷,這裡j就是(前面i個表達式累乘的表達式)里第j個變數,(這裡感謝一下seagg朋友給我指出的錯誤,大家可以看下留言處的討論)。如(1+x)(1+x^2)(1+x^3),j先指示的是1和x的係數,i=2執行完之後變為
(1+x+x^2+x^3)(1+x^3),這時候j應該指示的是合併后的第一個括弧的四個變數的係數。.
④ 、 k表示的是第j個指數,所以k每次增i(因為第i個表達式的增量是i)。
⑤ 、把c2的值賦給c1,而把c2初始化為0,因為c2每次是從一個表達式中開始的
目錄