數量分類學

發展初期數量分類方法先被表徵學派接受。60年代以後，數量分支分類也得到發展，數量分類學逐漸被愈來愈多的生物學家所接受，廣泛應用於生物分類中。數量分類學的產生在生物分類中提出定量的觀點，並採用數學方法。把分類學的研究從定性的描述提高到定量的綜合分析，對生物分類學的發展帶來重大影響。

基本觀點　分類必須有被分類的對象，分類的對象是由許多被分類的實體所組成的集合。如此被分類的實體是分類的基本單位，稱為運算分類單位，簡稱分類單位(OTU),由全部分類單位組成的集合稱為被分類群。分類還需要有分類的依據，分類的依據取決於被分類群中分類單位的性狀，所謂性狀，就是一個分類單位區分於其他分類單位的性質、特徵或屬性。分類單位在某個性狀所具有的狀態稱為性狀狀態，簡稱為狀態。例如種子植物某一屬的分類，可以取該屬的種或變種為運算分類單位。如果以花的顏色作為分類性狀，花所具有的不同顏色就是性狀狀態。分類就是將被分類群中所有分類單位，依據它們的性狀狀態作出劃分或聚合。經過分類獲得的分類單位集合，稱為分類群。

分類從形式上區分產生互相對立的概念：重疊與非重疊的分類，一元與多元的分類，劃分與聚合的分類，系統與非系統的分類。一個分類單位允許同時屬於不同分類群，稱這樣的分類為重疊的分類；依據一個性狀進行的分類稱為一元分類，綜合多個性狀獲得的分類是多元分類；分類獲得的分類群根據隸屬關係可以排成一定的系統，稱這樣的分類為系統分類。分類有兩種進行方式，從分類單位開始聚合為分類群稱為聚合的分類；先把被分類群看作是一個整體，再劃分為分類群，稱為劃分的分類。生物分類通常是非重疊的、多元的、系統的分類。數量分類學的分類方法常常採取聚合的分類。

生物分類與非生命事物的分類具有本質區別，生物分類學家追求理想的自然分類。然而什麼是真正自然的分類？如何達到這個目的？關於生物分類學中諸如此類的許多根本問題，分類學家意見不一致。50年代生物分類產生兩種對立的觀點，即表徵與分支兩種分類觀點。基於兩種不同的觀點，數量分類學產生兩種不同的數量分類方法。

表徵分類觀點由法國植物學家M.阿當松提出，這個觀點認為：作為分類的基礎，性狀愈多，包含的信息愈多，分類結果愈好；所有性狀對分類所起的作用都是同等重要；分類單位之間的全面相似性是許多性狀相似性比較的函數；分類是基於多種性狀全面的相似性。由於表徵分類的思想觀點與數學方法有許多共同之處，表徵分類學家最早使用數字工具和電腦技術從事分類學的研究。因此數量分類學中的表徵分類方法發展較早，比較完善。

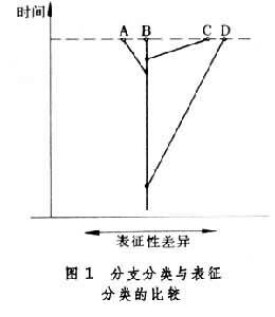
分支分類由德國昆蟲學家W.亨尼希提出，他的代表著《系統發育分類學》全面地闡述了分支分類觀點。他對當前的分類學進行批判，指出生物個體所表現的性狀與其演化關係不完全一致，因此表現性狀不可靠，生物分類的依據應該從演化的譜系中尋找。利用圖1 可以進一步說明這兩種不同的觀點。圖中A、B、C和D分別表示在同一時間水平上的四個演化分支，D最早分化出來，一般情形,D與B具有較大的表現性狀差異，最後分化出來的C,其表現性狀應更接近B，可是生物進化的速度並不完全一致，有可能在表現性狀上C更接近於D。對於這種情形，根據表徵性差異，將C與D歸屬於一個分類群，A與D歸屬於另一個分類群。如果從演化分支關係上去考慮，就認為C與D歸屬同一類不甚合理，而應將C與A、B同歸為一類，因為它們在演化的譜系關係上比較接近。

分支分類觀點提出來以後，得到許多分類學家的支持，並應用於分類實踐中，在數量分類學中產生了相應於分支類的數學方法。分支分類的數學方法起步較晚，理論與方法都不十分完善，有待發展。

數量表徵分類的一般過程　性狀編碼 為了使用數學工具進行分類，必須首先對性狀進行編碼，把全部性狀狀態的記錄都改換成數值。不同性狀分別採取不同的編碼方式：①數值性狀，如生物體的長度、體積、重量或實驗獲得的數據，如果這些數值的大小能夠體現分類學意義，通常不必編碼，直接使用。②二元性狀，表現為肯定和否定兩種對立狀態的性狀，分別以數值0和1編碼。通常肯定為1，否定為0。③有序多態性狀，表現為3種狀態以上，能排列為一定次序的性狀，按排列的次序分別以整數給予編碼。例如生物體表被毛性狀，分無毛、疏毛、多毛和密毛幾個狀態，分別以數值0,1,2和3表示。④無序多態性狀，表現為3種狀態以上，不能排列成一定次序的性狀。無序多態性狀表現複雜，編碼比較困難，可以根據性狀的實際意義作適當分解，再進行編碼。

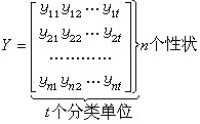
如果有t個分類單位,n個性狀，編碼后獲得的數據排成n行t列矩陣，這個矩陣稱為原始數值矩陣：

原始數據標準化 從編碼得到的原始數據，不同性狀的數值來源不同，單位和量綱不同，因而數值的大小和變化幅度不同。性狀之間的這種差異不具有分類意義，需要施行標準化變換給予消除，常用的變換計算如下:

其中平均值

標準差

xij表示變換后的新數據，相應的原來數據是yij。原始數值矩陣Y經標準化變換后，得新的數值矩陣：

相似性的定量表示 分類需要比較分類單位之間相親性的程度，描述這種相親性的相似性係數有以下幾類：距離係數、相關係數、聯合係數和信息係數等。各種係數的數學公式都是以不同的數學方法，從不同的角度綜合全部性狀，計算兩分類單位之間的相似性。例如平均歐氏距離係數

其中xki 和xkj 取自矩陣X的第k行，分別為第i和第j列元素；dij表示第i與第j分類單位之間的距離係數。

計算每一對分類單位的相似性係數，獲得一個t階對稱矩陣，稱為相似性矩陣。相似性矩陣包含了被分類類群中所有分類單位之間的相似性關係，分類運算將依據這種關係而進行。圖2中的數據為樺木科6個屬最早計算出來的相似性距離係數。

聚類運算通常採取聚合運演演算法。運算從相似性矩陣開始，最初把每一個OTU都看作是一個分類群，將最相似的類群歸併為新類群。如此重複多次歸併，直到所有OTUs都聚合在一起，每次聚合獲得新類群，需要計算它與其他類群的相似性係數。這裡是分類運算的關鍵，新相似性係數的計算是否合理，它將影響整個運算過程。不同的計算公式將引出不同的分類方法。可以將多種方法總結成統一的公式:

其中、、和表示相似性係數，下角標代表類群的編碼；兩個類群p與q結合成新類群r，i表示其他任一待計算的類群；αp、αq、β和ν是四個參數，每賦給一組參數值就確定一種聚類方法（見表）。

表中nr，np，nq和ni分別表示類群n,p，q和i的分類單位個數。

分類結果的表示 生物分類的結果包含有多個分類群層層隸屬的複雜關係，需要採取比較形象的表示方法。分類結果的表示依分類的方法而定，主分量分類法可採取坐標圖和體視圖，圖論分類可畫出最小生成樹圖，分類單位較多時可採取相似性矩陣圖。最通常的表示方法是樹譜圖。依表徵分類建立的樹譜圖稱為表徵樹譜圖。圖2給出了樺木科數據的樹譜圖（距離係數）。

數量分支分類　分支分類把分類的原則確立在生物演化的譜系關係上，得到許多生物學家的重視，相應的定量分類方法也獲發展。目前已經為分類學家採用的方法有W.H.瓦格納網路，J.H.卡明和R.R.索卡爾的單系法以及基於性狀加權的合諧法等。

數量分支分類與表徵分類方法完全不同，它的數學理論基礎是組合數學中的圖論，數學家正在努力建立一套從公理開始的，嚴謹的分支分類數學理論體系。1965年卡明和索卡爾提出簡約進化假設，它為數量分支分類奠定了一條基本原則。

為了得到符合譜系關係的分類結果，需要按照演化的次序，對分類性狀賦以非負整數編碼，通常把0定為原始狀態，編碼數值的增加與生物進化方向一致。圖3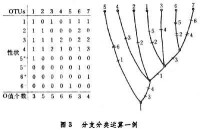中的數據是卡明和索卡爾從自己虛構的動物群體，為說明分類方法而構造的性狀編碼數據。旁邊的樹狀圖是該數據的分支分類計算結果。

按照分支譜系關係而建立的樹譜圖稱為分支樹譜圖。整個分支樹譜圖有一個共同的演化祖先，這是演化的起點，分支樹譜圖顯示出生物演化的關係。每一個演化分支的頂端都是現存的OTUs，兩個OTUs的最近共同祖先如果不屬於已知的分類單位，那就是為構造譜系圖而假設的，已經絕滅的祖先，稱為假設分類單位，簡作“HTU”，不論是分類單位抑或是假設分類單位都稱作分支單位或演化單位。如果性狀編碼每增加一個編碼值定為進化的度量單位“步”，分支樹譜圖中先後鄰接的兩個分支單位間，所有性狀進化的步數稱為該分支單位間的演化長度。按照簡約進化原則，對於一個分支分類問題，在所有可能的分支樹譜圖中符合真實演化情況的，全圖演化長度總和取最小值。追求最小演化長度成為設計分支分類運算方法的原則。單系法的運算步驟如下：

①　對每個分支單位計數性狀狀態為 0的個數。具有0數最多的分支單位意味與原始祖先最接近。

②　從數值矩陣中刪去具有0數最多的分支單位，然後找出數值矩陣中無0的性狀，若找不到無0的性狀，重新選擇下一個0數最多的分支單位給予刪除，必要時刪去兩個以上具有較多0值的分支單位，直到至少出現一個無0的性狀。

③　在分支譜系圖中作出相應於被刪去分支單位的分支。

④　找出無0值的性狀，凡此性狀從數據中都減去1，必要時重複減1，直到該性狀至少含有一個0。再將全部是0的性狀從矩陣中除去。

多次重複前面從1～4的步驟，每循環一次有部分分支單位被分支，直到全部分支單位都被分支為止。

分類的各種數學方法及其應用　數量分類學的廣泛應用，促使它的數學理論迅速發展，各種數學工具包括集合論、圖論、概率論、統計數學、線性代數、資訊理論和模糊數學都被引用進來，各種數學工具產生了不同的分類方法。方法的多樣性滿足各種應用的需要。

系統分類法 這是由幾何、代數和統計等運算組成的多種分類方法。至今已有 8種以上的方法被總結於統一的公式中（見表）。因而多種分類方法可以編寫在同一個電腦程序中，為分類工作帶來極大的方便。

系統分類法發展較早，理論和方法都比較完善，是一種比較成熟而定型的分類方法，在解決分類問題中廣為應用。

圖論分類法 組合數學中的圖論應用於分類產生了圖論分類法。圖論中的有向樹圖和賦權有向樹圖是利用數學方法描述生物演化關係的重要工具，從而圖論成為定量分支分類的數學理論基礎。有關分支分類的圖論研究發展很快。數學理論的發展，導出更完善的分支分類方法。圖論方法的另一個發展方向是利用賦權無向圖理論中的最小生成樹來表現生物分類關係。它也可用於表徵分類。

圖論分類法作為分支分類的工具廣泛應用於古生物，遺傳和進化理論的研究，70年代以後隨著分子生物學的發展，圖論分類法被應用於研究各種蛋白質和核酸等生物大分子的分類。從分子的水平上描述遺傳與進化的規律。圖論分類法很不完善，有待解決的問題很多，但是由於它的重要性，發展迅速。

主分量分類法 多元統計中主分量分析也應用於分類。在分類問題中，眾多性狀具有相關性，在性狀為坐標的多維空間中如果能找到一個方向，性狀在該方向上反映的離差變化最大，沿此方向就確定了一個向量稱為第一主分量，其次為第二、三、……主分量。這種方法猶如從多性狀的複雜事物中抓主要矛盾，利用抓主要矛盾的運算技巧，把一個多維的分類問題簡化為低維空間上的簡單問題。從而使分類問題迎刃而解。

主分量分類法發展較早，它的數學基礎是線性代數有關特徵值與特徵向量的內容，為了認識表現複雜的生物學問題它是一個十分得力的工具。圖4給出中國豬種主分量分析結果。通過分析指出，認識中國豬種的3個主要方面是豬體型大小，生殖能力和產肉脂肪率。相應於3個主分量的坐標圖中，畫出48個主要豬種的位置，對中國豬種給出十分形象的空間描述。主分量分類法不僅對生物分類，在生態學，環境科學以及農、林、醫等實際問題中都得到廣泛應用。

信息分類法 資訊理論也被用於分類，資訊理論中熵或信息量，這個概念可以描述生物類群的多樣性。較好的分類希望得到離散程度較小，傾向於清一色的類群，這就是信息分類的基本思想。

信息分類常用於生物地理學。在分子生物學，蛋白質分子中氨基酸的排列和核酸分子中核苷酸的排列都與電信編碼類似，從分子水平探索生物演化系統關係，信息分類有更廣闊前途。

模糊分類法 建立在模糊集合概念之上的分類方法稱為模糊分類法。由於許多生物表現性狀都屬於模糊概念，模糊分類更適合生物分類的需要。現在已應用於圖像識別等領域。