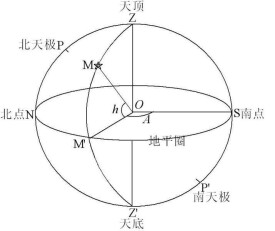
天球坐標系
天空中物體位置的坐標系
天球坐標系是天文學上用來描繪天體在天球上位置的坐標系統。有許多不同的座標系統都使用球面座標投影在天球上,類似於使用在地球表面的地理坐標系統。這些坐標系統的不同處只在用來將天空分割成兩個相等半球的大圓,也就是基面的不同。例如,地理坐標系統的基面是地球的赤道。每個坐標系統的命名都是依據其所選擇的基面。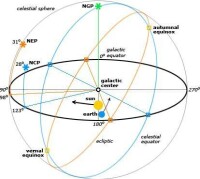

銀河、黃道與赤道坐標系統的方向,投影在天球上,顯示出銀河赤道 (黑色)、銀河北極 (NGP)、黃道 (橘色)、黃道北極 (NEP)、天球赤道 (藍色) 和天球北極 (NCP)。太陽和地球未依比例顯示,但是正確的呈現太陽環繞銀河中心的軌道方向,和地球環繞太陽的軌道方向
以天極和春分點作為天球定向基準的坐標系。
天球上各種球面正交坐標系的統稱。
坐標系統基面極坐標 地平 (也稱為Alt/Az或Az/El)地平面 天頂/天底 高度 (也稱為仰角) - 方位 - 子午圈 赤道 天球赤道 天極 赤緯 - 赤經或時角 黃道 黃道 黃極 黃緯 - 黃經 銀河 銀河平面 陰極 銀經 - 銀緯 超星系 超星系平面
在地平或高度方位系統,觀測者位於地球上,圍繞著自身的自轉軸每一恆星日 (23h56m) 相對於固定的恆星背景旋轉一周。在地平系統中,天體位置的定位主要用於計算出與沒的短暫時間,例如,太陽升起和沉沒時間的計算。過去它也用於導航,例如,確定行星位置的高度與方位,依據時間確定船隻正確的經度和緯度。許多望遠鏡也採用經緯儀的架台,然後依據時間、地理位置,利用電腦計算天體在地平上的位置 (高度和方位)。

地平坐標
赤道座標系統以地球的中心為中心並且固定住環繞我們的天空,因此它看起來與地球固定在一起,而我們在地球的表面上繞著自身的軸旋轉。赤道座標描述的天空,包括所見的太陽系,和現在所有的星圖幾乎全都用赤道座標來繪製,而古代的東方天文學家早已使用這種座標繪製星圖。
赤道系統是專業天文學家最常用的座標系統,業餘天文學家也使用赤道系統的架台在夜晚追蹤天空的運動。天體被調整好的望遠鏡或其它種類的儀器找到之後,這些天體就會使用與赤道座標匹配來標示它們的位置。
最常被選用的即和赤道系統是古老的1950分點或現代的2000分點,但也可以使用標示日期的極和赤道系統,意味著必須考量日期的需要,例如對一顆行星或太空船位置的測量。也有細分到"平均日"座標,它們採用平均值而忽略章動和包含章動的"真正日期"。
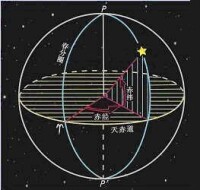
赤道坐標
黃道座標系統是一種古老的座標系統,使用在天文學和占星術上未分家前的星圖上,特別是在西方世界。
黃道系統描述的是行星環繞太陽移動的軌道,它的中心在太陽系的重心,也就是太陽的位置。它的基本平面是地球的軌道面,稱為黃道面。在行星科學中被大量使用,像是計算行星的位置和其他重要的行星軌道參數:傾角、升交點、降交點、近日點位置等等。
黃道坐標
在有關恆星動力學和星繫結構的某些理論工作中﹐常常採用一種球面坐標系──銀道坐標系
銀河系的主要部分是一個扁平的圓盤狀結構﹐它的平均平面稱為銀道面。銀道面是銀道坐標系的基本平面﹐它與天球相交的大圓稱為銀道﹐也就是銀道坐標系中的基圈。天球上與銀道相平行的小圓稱為銀緯圈。銀道的幾何極稱為銀極﹐又有南﹑北銀極之分。作為銀道坐標系的極是北銀極L ﹐過兩個銀極所作的半個大圓稱為銀經圈﹐也就是銀道坐標系中的副圈。所有的銀經圈都與銀道相垂直。銀道與天赤道在天球上相交於兩點。由北銀極向銀道面看去﹐按逆時針方向從赤道以南向北通過赤道的那一個點﹐稱為銀道對天赤道的升交點﹔另一點就是降交點。1958年以前﹐採用銀道升交點作為銀道坐標系的主點﹐過該點的銀經圈就是這一坐標系的主圈。
天體的銀經圈與銀道交於B 點﹐大圓弧B =b 就是天體在銀道坐標系中的第一坐標﹐稱為銀緯。由銀道起沿銀經圈向南北銀極分別量度銀緯b ﹐從0°~±90°﹐南銀緯取為負值。過升交點的銀經圈與天體的銀經圈所交的球面角L 或銀道上的大圓弧B = ﹐是天體在銀道坐標系中的第二坐標﹐稱為銀經。1958年以前﹐銀經由升交點起算﹐從0°~360°。量度方向是逆時針的﹐銀道坐標系也是一種左旋坐標系。
由於銀道面是銀河系的平均平面﹐需要對銀道的位置作出比較準確的測定。銀道坐標系的空間定向用銀極的赤道坐標來確定。1958年以前﹐北銀極在赤道坐標系中的坐標取為﹕
赤經 A =1240=190°
(1900.0曆元)。
赤緯 D =+28°
這樣規定的坐標系稱為舊銀道坐標系﹐系統內的銀道坐標用﹑b 表示。銀道與赤道的交角i =62°﹐稱為銀赤交角﹐升交點的赤經為1840。在1958年國際天文學聯合會第十屆大會上﹐根據新的觀測資料﹐規定北銀極赤道坐標的新值為﹕
赤經 A =1249=192°15
(1950.0曆元)。
赤緯 D =+27°24
同時規定﹐銀經不從升交點量起﹐而取銀河中心方向(人馬座)為銀經的起算點﹐該方向在舊系統內的坐標為﹕
=32769﹐ b =-140 。
量度方式仍按左旋坐標系的規定。這樣規定的坐標系稱為國際天文學聯合會銀道坐標系﹐該坐標系內的銀經﹑銀緯用﹑b 表示﹐以別於舊系統內的﹑b 。
各種天球坐標系之間的關係 第一赤道坐標系和第二赤道坐標系的關係 這兩種系統的第一坐標都是赤緯﹐它們的第二坐標﹐即時角t 和赤經α之間的關係為﹕
s =t +α﹐
式中s =F 為春分點Υ 的時角﹐即測站的地方恆星時。
地平坐標系和赤道坐標系之間的關係 可根據圖 2的球面三角P Z 用球面三角的公式來表示﹕
cosz =sin sin +cos cos cost ﹐
sinα sinz =cos sint ﹐
cosα sin =-cos sin +sin cos cost ﹐
式中 =Z 為天體的天頂距﹔ =90°-PZ 為測站的地理緯度。
赤道坐標系和黃道坐標系之間的關係 黃道坐標系在天體力學中有廣泛的用途﹐但天體的黃道坐標通常不是直接觀測量。另一方面﹐用黃道坐標表示的某些理論結果﹐也往往要先化為赤道坐標﹐然後才能實際應用。因此﹐必須建立這兩種坐標系之間的轉換關係。黃道坐標系和赤道坐標系之間的轉換﹐可根據圖3按球面三角的有關公式來完成。
赤道坐標系和銀道坐標系之間的關係 天體的銀道坐標也不是直接觀測量﹐對某些恆星天文工作﹐需要建立其同赤道坐標之間的聯繫。這種聯繫﹐可根據圖4用球面三角的有關公式來完成。銀道坐標與赤道坐標之間的轉換並不要求有很高的精度﹐有專門的換算表可用﹐這一點與其他坐標系之間的換算是不同的。
空間坐標系及其換算 在某些天文問題中﹐不僅要知道天體在天球上的二維投影位置﹐而且還必須知道它的空間位置﹐比如有關人造衛星運動的研究就是如此﹐因而需要建立空間三維坐標系﹐包括三維直角坐標系和三維球坐標系﹐後者又稱為三維極坐標系。不論哪一種空間坐標系﹐它們的原點總是與天球的中心相重合﹐這與二維球面坐標系中的原點(即主點)是不同的。
三維極坐標系統是在二維球面坐標系的基礎上增加一條向徑r構成的﹐向徑是坐標原點到所研究的天體的線距離。人造衛星的空間位置可以用它的赤經﹑赤緯和向徑唯一地加以確定﹐因相應的二維球面坐標系的不同﹐所以又有三維赤道球坐標和三維黃道球坐標等不同的球坐標系統。
三維直角坐標系又稱為空間直角坐標系。在通常情況下﹐為便於與相應的球坐標系進行坐標轉換﹐空間直角坐標系OXYZ 的OZ 軸取球面坐標系的極點所在的方向﹐OX 軸取主點所在的方向﹐OXY 平面與基圈相重合﹐而OXZ 平面與主圈相重合。這時﹐空間坐標與相應的二維球坐標或三維球坐標之間有最簡單的關係。另外﹐對應於不同的二維球面坐標系﹐也可以有不同的空間直角坐標系﹐如赤道直角坐標系﹑黃道直角坐標系等。
空間坐標系的轉換包括﹕對應於同一球面坐標系統的空間直角坐標系和空間球坐標系之間的轉換﹔不同空間直角坐標系之間的轉換﹔對應於不同的二維球面坐標系的空間直角坐標和空間球坐標之間的轉換﹔原點不同(如地心﹑日心等)的坐標轉換。
相對坐標系 在研究鄰近天體的相對位置及其運動狀態時﹐往往要使用相對坐標系﹐它又稱為微分坐標系。用相對坐標系研究的不是天體在天球上的具體位置﹐而是一個天體相對於附近另一個天體的相對位置。以赤道坐標係為例﹐兩個天體S (α﹐和S (α﹐)之間的相對關係
α=α-α=sin p sec ﹐
=-=cos p 。
稱 =sin p ﹐ =cos p 為天體S 相對於天體S 的直角坐標。這裡﹐兩天體之間的球面距離為一小量﹐﹑和 均以角秒為單位。S S P為一窄球面三角形。
銀河系統是以我們的太陽係為中心,指向銀河中心的方向為是0點的位置,而基本平面大致上與銀河盤面一致,但是有固定的標準。當然,銀河系統是用來決定星際物體在銀河中的相關位置。
經由會議決定,超星系的經度和緯度類比於銀河座標系統的銀經(l)和銀緯(b),分別標示為SGL和SGB,座標經度的起點(SGL=0)定義為銀河平面與超星系平面的交叉點。
地平緯度,也可以稱為高度角或仰角,指的是從天文地平線 (0°) 垂直向上量取到天頂 (+90°) 的角度。它還可以用負值延伸到地平線下最低點的天底 (-90°)。雖然有些地方會使用高度一詞取代仰角,但高度通常會被理解為一種直線單位的距離,像是米 (米,或是任何其他的長度單位),並不建議將它當成是一個角度的距離。
赤道座標轉地平座標
令δ為赤緯,H 為時角.
令φ為觀察者所在的地理緯度.
令a為高度角,A為方位角.
令θ是天頂 (或是天頂距,也就是仰角(Alt)90°的餘角)。
因此轉換的方程式是:
轉換方程
注意:反餘弦有兩組解,例如160° 和200°有相同的餘弦值,所以需要作個判別。如果H < 180°(或徑度量的π),則從上式得到的Az要修正為 Az = 360° - Az。
方位角
傾角
古在機制
軌道傾角變化