共找到2條詞條名為系統辨識的結果 展開
- 數學模型
- 書籍
系統辨識
數學模型
系統辨識是根據系統的輸入輸出時間函數來確定描述系統行為的數學模型。現代控制理論中的一個分支。通過辨識建立數學模型的目的是估計表徵系統行為的重要參數,建立一個能模模擬實系統行為的模型,用當前可測量的系統的輸入和輸出預測系統輸出的未來演變,以及設計控制器。對系統進行分析的主要問題是根據輸入時間函數和系統的特性來確定輸出信號。
system identification
對系統進行控制的主要問題是根據系統的特性設計控制輸入,使輸出滿足預先規定的要求。而系統辨識所研究的問題恰好是這些問題的逆問題。通常,預先給定一個模型類μ={M}(即給定一類已知結構的模型),一類輸入信號u和等價準則J=L(y,yM)(一般情況下,J是誤差函數,是過程輸出y和模型輸出yM的一個泛函);然後選擇使誤差函數J達到最小的模型,作為辨識所要求的結果。系統辨識包括兩個方面:結構辨識和參數估計。在實際的辨識過程中,隨著使用的方法不同,結構辨識和參數估計這兩個方面並不是截然分開的,而是可以交織在一起進行的。
先驗知識指關於系統運動規律、數據以及其他方面的已有知識。這些知識對選擇模型結構、設計實驗和決定辨識方法等都有重要作用。用於不同目的的模型可能會有很大差別。
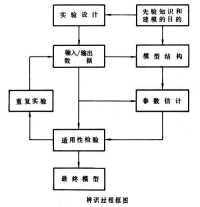
系統辨識
其次,建模的目的對於確定模型的結構和辨識方法也有重要意義。用於不同目的的模型可能會有很大的差別。在估計具有特定物理意義的參數時,主要考慮模型的參數值與真實的參數值是否一致。在建立預測模型時,只需要考慮預測誤差。在建立模擬模型時,就要根據應用的要求去決定模擬的深度,也就是決定模型結構的複雜程度。而對於設計控制系統的模型,則出於不同的控制目的可選擇不同的模型類。
辨識是從實驗數據中提取有關係統信息的過程,設計實驗的目標之一是要使所得到的數據能包含系統更多的信息。主要包括輸入信號設計,採樣區間設計,預採樣濾波器設計等。
辨識的基礎是輸入和輸出數據,而數據來源於對系統的實驗和觀測,因此辨識歸根到底是從數據中提取有關係統的信息的過程,其結果是和實驗直接聯繫在一起的。設計實驗的目標之一是要使所得到的數據能包含系統的更多的信息。為此,首先要確定用什麼準則來比較數據的好壞。這種準則可以是從辨識的可行性出發的,也可以是從某種最優性原則出發的。實驗設計要解決的問題主要是:輸入信號的設計,採樣區間的設計,預採樣濾波器的設計等(見系統辨識實驗設計)。
即選擇模型類中的數學模型M的具體表達形式。除線性系統的結構可通過輸入輸出數據進行辨識外,一般的模型結構主要通過先驗知識獲得。
知道模型的結構后,用輸入輸出數據確定模型中的未知參數。實際測量都是有誤差的,所以參數估計以統計方法為主。
造成模型不適用主要有三方面原因:模型結構選擇不當;實驗數據誤差過大或數據代表性太差;辨識演演算法存在問題。檢驗方法主要有利用先驗知識檢驗和利用數據檢驗兩類。
在提出和解決一個辨識問題時,明確最終使用模型的目的是至關重要的。它對模型類(模型結構)、輸入信號和等價準則的選擇都有很大的影響。通過辨識建立數學模型通常有四個目的。
①估計具有特定物理意義的參數 有些表徵系統行為的重要參數是難以直接測量的,例如在生理、生態、環境、經濟等系統中就常有這種情況。這就需要通過能觀測到的輸入輸出數據,用辨識的方法去估計那些參數。
系統辨識
③預測 這是辨識的一個重要應用方面,其目的是用迄今為止系統的可測量的輸入和輸出去預測系統輸出的未來的演變。例如最常見的氣象預報,洪水預報,其他如太陽黑子預報,市場價格的預測,河流污染物含量的預測等。預測模型辨識的等價準則主要是使預測誤差平方和最小。只要預測誤差小就是好的預測模型,對模型的結構及參數則很少再有其他要求。這時辨識的準則和模型應用的目的是一致的,因此可以得到較好的預測模型。
④控制 為了設計控制系統就需要知道描述系統動態特性的數學模型,建立這些模型的目的在於設計控制器。建立什麼樣的模型合適,取決於設計的方法和準備採用的控制策略。
經典的系統辨識方法的發展已經比較成熟和完善,他包括階躍響應法、脈衝響應法、頻率響應法、相關分析法、譜分析法、最小二乘法和極大似然法等。其中最小二乘法(LS)是一種經典的和最基本的,也是應用最廣泛的方法。但是,最小二乘估計是非一致的,是有偏差的,所以為了克服他的缺陷,而形成了一些以最小二乘法為基礎的系統辨識方法:廣義最小二乘法(GI S)、輔助變數法(IV)、增廣最小二乘法(EI,S)和廣義最小二乘法(GI S),以及將一般的最小二乘法與其他方法相結合的方法,有最小二乘兩步法(COR—I S)和隨機逼近演演算法等。
經典的系統辨識方法還存在著一定的不足: (1)利用最小二乘法的系統辨識法一般要求輸入信號已知,並且必須具有較豐富的變化,然而,這一點在某些動態系統中,系統的輸入常常無法保證;(2)極大似然法計算耗費大,可能得到的是損失函數的局部極小值;(3)經典的辨識方法對於某些複雜系統在一些情況下無能為力。
隨著系統的複雜化和對模型精確度要求的提高,系統辨識方法在不斷發展,特別是非線性系統辨識方法。主要有:
1、集員系統辨識法
在1979年集員辨識首先出現於Fogel 撰寫的文獻中,1982年Fogel和Huang又對其做了進一步的改進。集員辨識是假設在雜訊或雜訊功率未知但有界UBB(Unknown But Bounded)的情況下,利用數據提供的信息給參數或傳遞函數確定一個總是包含真參數或傳遞函數的成員集(例如橢球體、多面體、平行六邊體等)。不同的實際應用對象,集員成員集的定義也不同。集員辨識理論已廣泛應用到多感測器信息融合處理、軟測量技術、通訊、信號處理、魯棒控制及故障檢測等方面。
2、多層遞階系統辨識法
多層遞階方法的主要思想為:以時變參數模型的辨識方法作為基礎,在輸入輸出等價的意義下,把一大類非
線性模型化為多層線性模型,為非線性系統的建模給出了一個十分有效的途徑。
3、神經網路系統辨識法
與傳統的基於演演算法的辨識方法相比較,人工神經網路用於系統辨識具有以下優點:(1)不要求建立實際系統的辨識格式,可以省去對系統建模這一步驟;(2)可以對本質非線性系統進行辨識;(3)辨識的收斂速度僅與神經網路的本身及所採用的學習演演算法有關;(4)通過調節神經元之間的連接權即可使網路的輸出來逼近系統的輸出;(5)神經網路也是系統的一個物理實現,可以用在在線控制。
4、模糊邏輯系統辨識法
模糊邏輯理論用模糊集合理論,從系統輸入和輸出的量測值來辨識系統的模糊模型,也是系統辨識的一個新的
和有效的方法,在非線性系統辨識領域中有十分廣泛的應用。模糊邏輯辨識具有獨特的優越性:能夠有效地辨識複雜和病態結構的系統;能夠有效地辨識具有大時延、時變、多輸入單輸出的非線性複雜系統;可以辨識性能優越的人類控制器;可以得到被控對象的定性與定量相結合的模型。模糊邏輯建模方法的主要內容可分為兩個層次:一是模型結構的辨識,另一個是模型參數的估計。典型的模糊結構辨識方法有:模糊網格法、自適應模糊網格法、模糊聚類法及模糊搜索樹法等。
5、小波網路系統辨識法
小波網路是在小波分解的基礎上提出的一種前饋神經網路口,使用小波網路進行動態系統辨識,成為神經網路辨識的一種新的方法。小波分析在理論上保證了小波網路在非線性函數逼近中所具有的快速性、準確性和全局收斂性等優點。小波理論在系統辨識中,尤其在非線性系統辨識中的應用潛力越來越大,為不確定的複雜的非線性系統辨識提供了一種新的有效途徑,其具有良好的應用前景。
通過參數估計得到的模型,雖然按某種準則在選定的模型類中是最好的,但是並不一定能達到建模的目的,所以還必須進行適用性檢驗。這是辨識過程的重要一環,只有通過適用性檢驗的模型才是最終的模型。
造成模型不適用主要有三個方面的原因:模型類(模型的結構)選擇不當;實驗數據誤差過大或由於實驗條件限制,數據的代表性太差;辨識演演算法存在問題(例如沒有考慮必要的約束)。
模型是否適用與建模的目的緊密相關,所以很難得出統一的檢驗方法,而是要根據問題的性質採取不同的方法。一般來說,適用性檢驗在得到模型後進行,但也可以在辨識過程的各個階段進行。例如,考察模型的結構可辨識性本身就是一種適用性檢驗,不可辨識的模型當然是不適用的。
適用性檢驗的方法主要有兩類:利用先驗知識檢驗和利用數據檢驗。利用先驗知識是適用性檢驗的一條重要途徑。有一些模型從數據的擬合上看不出問題,但是根據對模型已有的知識卻可以斷定模型是否適用。例如辨識一個化學反應動力學模型:已經知道反應物濃度增大並不抑制反應,如果參數估計的結果反應係數是負的,就可斷定這是不合理的。又如辨識生理動力學模型:如果參數估計得到的參數值已超過生理學已知的可能範圍,這樣的模型也是不適用的。適用性檢驗的另一條途徑是,利用數據在同一模型類中或在不同的模型類中進行比較。在得到模型后常常用一組不同於辨識時用的數據去檢驗模型的精度。如果檢驗的結果有過大的誤差,則可能存在兩個問題:辨識用的數據缺乏代表性或所選的模型類不合適。在不同類的模型中進行比較所用的方法主要是統計檢驗(如F檢驗、似然比檢驗)或者是在擬合誤差的基礎上加上評價模型的懲罰項(如赤池的AIC準則)。
凡是需要通過實驗數據確定數學模型和估計參數的場合都要利用辨識技術,辨識技術已經推廣到工程和非工程的許多領域,如化學化工過程、核反應堆、電力系統、航空航天飛行器、生物醫學系統、社會經濟系統、環境系統、生態系統等。適應控制系統則是辨識與控制相結合的一個範例,也是辨識在控制系統中的應用。