布里淵區

固體的能帶理論中，各種電子態按照它們的波矢分類。在波矢空間中取某一倒易陣點為原點，作所有倒易點陣矢量的垂直平分面，這些面波矢空間劃分為一系列的區域：其中最靠近原點的一組面所圍的閉合區稱為第一布里淵區；在第一布里淵區之外，由另一組平面所包圍的波矢區叫第二布里淵區；依次類推可得第三、四、…等布里淵區。各布里淵區體積相等，都等於倒易點陣的元胞體積。周期結構中的一切波在布里淵區界面上產生布拉格反射，對於電子德布羅意波,這一反射可能使電子能量在布里淵區界面上（即倒易點陣矢量的中垂面）產生不連續變化。根據這一特點,1930年L.-N.布里淵首先提出用倒易點陣矢量的中垂面來劃分波矢空間的區域，從此被稱為布里淵區。

第一布里淵區就是倒易點陣的維格納－賽茨元胞，如果對每一倒易點陣作此元胞，它們會毫無縫隙的填滿整個波矢空間。由於完整晶體中運動的電子、聲子、磁振子、……等元激發（見固體中的元激發）的能量和狀態都是倒易點陣的周期函數，因此只需要用第一布里淵區中的波矢來描述能帶電子、點陣振動和自旋波……的狀態，並確定它們的能量（頻率）和波矢關係。限於第一布里淵區的波矢稱為簡約波矢，而第一布里淵區又叫簡約區，在文獻中不加定語的布里淵區指的往往就是它。

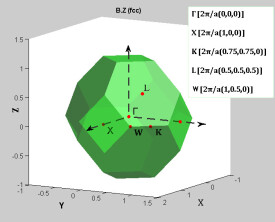
布里淵區的形狀取決於晶體所屬布喇菲點陣的類型。簡單立方、體心立方和面心立方點陣的簡約區分別為立方體，菱十二面體和截角八面體（十四面體）。它們都是對稱的多面體，並具有相應點陣的點群對稱性，這一特徵使簡約區中高對稱點的能量求解得以簡化（見晶體的對稱性）。

簡約布里淵區（Reduced Brillouin zone）：

由於晶體中的格波或者電子波的色散關係在波矢空間是周期為π/a的周期性函數（例如，E(k) = E(k+π/a)，則k和k+π/a表示相同的狀態；因此可把波矢限制在第一Brillouin區(－π/a < q < π/a ) 內，而將其他區域通過移動n/a而合併到第一Brilouin區；在考慮能帶結構時, 只需要討論第一Brilouin區就夠了。這時的第一Brillouin區也就稱為簡約布里淵區。

簡約布里淵區中的一個波矢可能對應有幾個不同的能量狀態。該區域內的波矢即稱為簡約波矢。簡約布里淵區的形狀因晶體結構而異；實際上可由晶格的倒格子的Wigner-Seitz原胞給出。金剛石結構的Si、Ge和閃鋅礦結構的Ⅲ-Ⅴ族半導體等, 都具有面心立方Bravais格子, 因此都具有體心立方的倒格子, 從而也都具有相同形狀的第一Brilouin區, 為截角八面體(即是由6個正方形和8個正六邊形構成的14面體)。

在各種周期性邊界條件的第一原理計算方法中，需要涉及到在布里淵區的積分問題，例如總能、電荷密度分佈，以及金屬體系中費米面的確定等等。如果採用普通的在布里淵區內均勻選取k點的方法，那麼為了得到精確的結果點的密度必須很大，從而導致非常大的計算量。這使得計算的效率非常低下。因此，需要尋找一種高效的積分方法，可以通過較少的點運算取得較高的精度。而這些k點被稱之為“平均值點”（Baldereschi）或者“特殊點”（Chadi, Cohen）。

1、Chadi和Cohen最早提出了這種特殊點的數學基礎。

2、考慮一個光滑函數，我們可以將其展為傅立葉級數：假設另有一個擁有體系全部對稱性（對稱性用對稱群表示）的函數，滿足條件，則 我們可以將用展開如下：其中是對稱群的階數。設，將上式的求和順序重新組合可以得到其中是距離原點第近鄰的球半徑，按升序排列，且。需要注意的是限制條件 具有球對稱性，也即高於的對稱性，所以滿足限制條件的格點集合併不一定都是等價的——或說可以通過中的操作聯繫起來的——格點。方程(3)中的函數滿足下列條件：上式中是倒格矢，是滿足條件的格點數。五個方程分別表明函數在第一布里淵區內成奇函數、具有正交性、周期性、體系對稱性和完備性。對於特殊點法而言，前兩條更為重要。注意到上面公式中的求和從1開始，因此需要對的情況進行單獨定義。

3、我們定義，則函數的平均值為：那麼該如何得到呢？注意方程(3)，如果存在這樣的特殊點，使其滿足：>那麼立刻可以得到，這樣的點被稱為“平均值點”。但是普遍的講，滿足上述條件的點並不存在。對這個問題的解決辦法就是不用單個點，而採用滿足一定條件的k點的集合，利用這些點上函數值的加權平均計算。也即：其中可以取有限值。

4、利用方程(3)左右端的兩個式子，可以得到：根據方程(7)，可以得到考慮到隨的增大迅速減小的性質，我們可以近似的得到的平均值：而將方程(9)的第二項作為可控誤差。因此，如果我們可以找到一組點，使得(1)集合中的點盡量少；(2)這些點在盡量大的情況下滿足方程(7)，則我們進行布里淵區積分的時候可以儘可能快的得到精度較高的結果。這正是特殊點方法的要點所在。反過來講，這也表明進行具體計算的時候我們需要對計算精度進行測試，也即保證所取點使得上式的第二項足夠小。

5、Chadi-Cohen方法上一節證明了點的可行性。Chadi和Cohen首先提出了一套可以得出這些特殊點的方法。

首先找出兩個特殊點——，二者分別在和的情況下滿足然後通過這兩個點構造新的點集合：且權重為。下面證明在的情況下仍然滿足方程(7)：根據和的定義，可知對於和，也即上式等價於因此可以用這種方法產生一系列點，用以計算布里淵區內的積分。如果此時的精度不夠，則利用同樣的方法繼續生成新的點集合：其中為在情況下滿足的特殊點。從而改進精度。

6、事實上，如果考慮體系的對稱性，則中的點數目可以極大的減小。也就是說，對於給定的點，可以找出其波矢群，階數為，那麼實際上按上述方法構造出來的只有個不同的點，此時各點上的權重為。更進一步，通過點群的全部對稱操作，可以將全部的點轉入第一布里淵區的不可約部分。如果點的重疊度（即第一布里淵區不可約部分中佔有同樣位置的點個數）是，則在最後的計算中，這個點的權重為

上述Chadi-Cohen方法非常巧妙，但是在具體的應用上必須首先確定23個性能比較好的點，由此構建出的點集合才擁有比較高的效率和精度。因此，對於每一個具體問題，在計算之前都必須經過相當的對稱性上的分析。對於編寫程序而言，這是一件很麻煩的事情。那麼，是否存在一種比較簡易的產生點網格的方法，同時又滿足方程(7)呢？答案是肯定的，這就是通常所說的Monkhorst和Pack方法[2]。

晶體中的格點總可以表述為，其中是實空間三個方向上的基矢。Monkhorst和Pack建議按如下方法劃分佈里淵區

將點寫為分量形式，則可得到如下表達式

其中是倒空間的基矢。與Chadi-Cohen方法相似，Monkhorst和Pack定義函數為：

>

則相應於Chadi-Cohen方法中的，我們可以計算在如方程(12)所生成的離散化的網格點的相同的量：

其中

注意到都是整數，因此可以算出：

其中第三種情況是因為是奇函數。引入限制條件： <; < 則可得：

也即在點網格上是正交的。與Chadi-Cohen方法類似，將函數用展開：

同時左乘並在布里淵區內積分，可得

因為，所以從方程(19)可得

忽略前面的常數因子，可以看到Monkhorst-Pack方法中的表達式與Chadi-Cohen方法完全一樣。現在將的表達式代入上述方程，則

因此

其中

與我們在Chadi-Cohen方法中看到的一樣，在第一布里淵區的平均值可以用近似（在Chadi-Cohen方法中是）。而且誤差（方程右邊第二項）可控，即可以通過增加點密度的方法提高精度。這是因為增大，根據上面所述的取值可知，在更大的時候仍能保證方程(7)成立。

但是根據方程(3)可得

如果值取得比較大，那麼所需計算的點數目就會非常大，如何提高Monkhorst-Pack方法的效率呢？考慮到體系的對稱性，則點的數目會大大的減少。重新寫出如下：

其中是體系所屬點群階數與點的波矢群階數的比值：。是對所有點進行對稱及平移操作后第一布里淵區中所有不重合的點數。進一步考慮不可約部分，那麼通過改變（變為，其中定義見上節）可以進一步減少。因為處於高對稱位置上的點其波矢群階數也比較高，因此相應的這些高對稱點的權重就比較小。這也是為什麼在VASP的OUTCAR文件中高對稱的點權重比較小的理論根本，也是特殊點法盡量避開高對稱點的原因所在。與Chadi-Cohen方法一樣，的大小是Monkhorst-Pack方法效率高低的重要標誌。文獻中給出了bcc以及fcc兩種格子中的：

BCC:

FCC:

可以看出，即使對於較大的值，也是比較小的，因此Monkhorst-Pack方法效率是比較高的。

應該注意的是，Monkhorst-Pack方法的關鍵一點是將三維空間的問題轉化為三個獨立的一維問題。因此，對於六角格子或者單斜格子，基矢之間不正交，上述Monkhorst-Pack方法並不適用，而必須加以修改[3]。以六角格子為例，Pack指出點網格應按下述方法生成[4]：

也即軸和軸分別設置。相應的，的大小可計算如下：

上述生成點的方法對應於VASP手冊中對於點設置的建議“對於六方體系應該將點置於原點處”。

需要強調的是，我們在以上所討論的所有對稱性均指純旋轉操作，也即點群對稱性。因此，對於同屬一種晶系而屬於不同空間群的兩種體系而言，其操作可能並不一致。

Cunningham[5]對於二維情況依照Chadi-Cohen方法分別生成了點集合。我們選擇四方格子和正方格子兩種情況進行具體的分析。

實空間和倒空間的基矢及格點坐標分別為：

選擇（或為奇數時）以及（或為奇數時）這個格子的對稱操作為，按照Chadi-Cohen方法，可以構建點如下：

每個點的權重。

將上例中的，則四方格子轉變為正方格子。兩種情況最主要的不同是布里淵區不可約部分有了變化，從上式可以看出，在正方格子下，,和重合。因此只有三個不同的點，每個點的權重為，而且。

利用特殊點計算電荷密度

將Bloch函數用Wannier函數展開，有[6]：

則在給定點的電荷密度為：

而

我們重寫如下：

其中求和號中的表明而且。因此，考慮到對稱性，又可寫為：

上式中，第一項與和無關，相當於Chadi-Cohen方法中的。而第二項中因為對所有的求和，因此可以將這一項寫為如下形式：

上式中與無關，且隨增大而遞減，相當於。因此可寫為

如果存在，滿足，則立即可以得到

但是普遍的講，這樣的並不存在。例如，在fcc格子中考慮第一、二、三近鄰，寫出：

不存在單獨的點同時滿足上述三個方程。因此，需要尋找一系列特殊的點，滿足

則。

Chadi和Cohen[6]採用、和三個點計算的值：，取得了較好的結果。而在文獻1中，他們利用和改進了計算結果：。