平面角

幾何之父歐幾里得曾定義角為在平面中兩條不平行的直線的相對斜度。普羅克魯斯認為角可能是一種特質、一種可量化的量、或是一種關係。歐德謨認為角是相對一直線的偏差，安提阿的卡布斯認為角是二條相交直線之間的空間。歐幾里得認為角是一種關係，不過他對直角、銳角或鈍角的定義都是量化的。

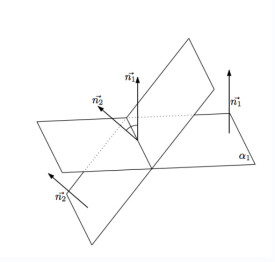
平面角是以二面角的棱上任意一點為端點，在兩個面內分別作垂直於棱的兩條射線，這兩條射線所成的角叫做二面角的平面角。

或者從二面角的棱上任一點在兩個半平面內分別作垂直於棱的射線，則這兩條射線所成的角叫做二面角的平面角。

1.二面角就是用它的平面角來度量的。一個二面角的平面角多大，我們就說個二面角是多少度的二面角。

2.二面角的平面角與點（或垂直平面）的位置無任何關係，只與二面角的張角大小有關。

角通常用三個字母表示：兩條邊上的點的字母寫在兩旁，頂點上的字母寫在中間。概述圖中的角用∠AOB表示。但若在不會產生混淆的情形下，也會直接用頂點的字母表示，例如角∠O。

在數學式中，一般會用希臘字母（α,β,γ,θ,φ, ...）表示角的大小。為避免混淆，符號π一般不用來表示角度。

常見測量單位

以角的端點為圓心做圓弧。由於圓弧的半徑和弧長成正比，而角是長度的比例，所以圓的大小不會影響角的測量。

● 弧度：用角在圓上所切出的圓弧的長度除以圓的半徑，一般記作rad。弧度是國際單位制中規定的角的度量，但卻不是中國法定計量單位，角度則是角在中國的法定計量單位。此外，弧度在數學及三角學中有廣泛的應用。

● 角度：由角在圓上所切出的圓弧的長度除以圓的周長再乘以360的結果，一般用°來標記，讀作“度”。一度可以繼續分為60“分”或3600“秒”。角度在天文學和全球定位系統中有重要應用。

● 梯度：是角在圓上所切出的圓弧的長度除以圓的周長再乘以400的結果。

其他測量單位

角度的量測可以視為弧長s和半徑r的比例，再依選用單位乘以一比例係數。

例如以上的弧度、角度和梯度，其轉換係數n分別為、360和400。

以下是一些其他的測量單位，對應不同的n值。

● 圈數或轉數（）：是指完整旋轉一圈，依應用的不同，會簡寫為cyc、rev或rot，不過在每分鐘轉速（RPM）的單位中，只用一個字母r表示。

● 直角（）：是1/4圈，是幾何原本中用的角度單位，在德文中曾用表示直角。

● 時角（）：）常用在天文學中，是圈。此系統是用在一天一個周期的循環（例如星星的相對位置），其六十進位下的子單位稱為“時間分角”及“時間秒角”，這兩個單位和角度的角分及角秒不同，前者大小為後者的十五倍。

● 米位（）：此單位是指一個單位大約等於毫弧度的角度，有許多不同的定義，其數值從0.05625度到0.06度（3.375至3.6角分），而毫弧度約為0.05729578度（3.43775角分）。在北大西洋公約組織的國家中，米位定義為圓的。其數值大約等於一個角度的弧長為一米，其半徑為一公里的角度（）。

● 角分（）：定義為一度的，是圈，會用′表示，例如等於 度，也就是3.5度，有時也會出現小數，例如度。海里曾定義為在地球的大圓上一角分的弧長。

● 角秒（）：定義為一角分的，會用″表示，例如等於度，或是3.125度。

正角和負角

以上角的定義均未考慮數值為負的角。不過在一些應用時，會將角的數值加上正負號，以標明是相對參考物不同方向的旋轉。

在二維的笛卡兒坐標系中，角一般是以x軸的正向為基準，若往y軸的正向旋轉，則其角為正角，若往y軸的負向旋轉，則其角為負角。若二維的笛卡兒坐標系也是x軸朝右，y軸朝上，則逆時針的旋轉對應正角，順時針的旋轉對應負角。

一般而言，−θ角和一圈減去θ所得的角等效。例如−45°和等效，但這隻適用在用角表示相對位置，不是旋轉概念時。旋轉−45°和旋轉315°是不同的。

在三維的幾何中，順時針及逆時針沒有絕對的定義，因此定義正角及負角時均需列出其參考的基準，一般會以一個通過角的頂點，和角所在平面垂直的向量為基準。

在導航時，導向是以北方為基準，正向表示順時針，因此導向45°對應東北方。導向沒有負值，西北方對應的導向為315°。

量測角的方法

除了量測角本身的大小外．也有其他的方式，可以量測角的大小。

坡度等於一個角的正切值，常用百分比或千分比來表示。當一個角的坡度小於5%時，其坡度近似於角以弧度表示的數值。

在有理幾何學中，一個角的大小是以伸展度（spread）來表示，伸展度定義為角對應正弦的平方，而任一角正弦的平方和該角補角正弦的平方相等。因此任一角和其補角在有理幾何學中是等同的。

● 零角角度等於0°,或一條線

● 銳角角度大於0°且小於90°，或弧度大於0且小於的角。

● 直角角度等於90°，或弧度為的角。

● 鈍角角度大於90°且小於180°，或弧度大於且小於π的角。

● 平角角度等於180°，或弧度為的角。

● 優角或反角角度大於180°且小於360°，或弧度大於且小於的角。

● 周角角度等於360°，或弧度為的角。

求二面角的大小是考試中經常出現的問題，而用三垂線法作二面角的平面角是求二面角大小的一個重要方法，許多同學在解題過程中由於沒有有效地利用三垂線定理（或逆定理）作出二面角的平面角，使得解題受阻．

我們把用三垂線定理（或逆定理）作二面角的平面角的方法稱為三垂線法，其作圖模型為：

在二面角－l－中，過平面內一點A作AO⊥平面，垂足為O，過點O作於B（過A點作AB⊥於B），連結AB（或OB），由三垂線定理（或逆定理）知（或），則∠ABO為二面角。—l—的平面角。

作圖過程中，作出了兩條垂線AO與OB（或AB），后連結AB兩點（或OB兩點），這一過程可簡記為“兩垂一連”，其中AO為“第一垂線”．“第一垂線”能否順利找到或恰當作出是用三垂線法作二面角的平面角的關鍵，在具體解題過程中要注意以下幾點：

1．善於利用圖中已有的“第一垂線”

例1 已知斜三稜柱中，，在底面ABC的射影恰為AC的中點M，又知與底面ABC所成的角為60°．

⑴求證：BC⊥平面；

⑵求二面角的大小．

剖析：注意該題的第⑴問，事實上本題已經暗示了BC就是我們要尋求的“第一垂線”．

略解2 與底面AB成的角為60°，所以又M是AC中點，所以是正三角形，作於N，點N為的中點，連結BN，由BC⊥平面則∠BNC為二面角的平面角．設正的邊長為a，所以，在中，，即 .

例2 在底面是直角梯形的四稜錐中，SA⊥面ABCD，

⑴求四稜錐S—ABCD的體積；

⑵求面SCD與面SBA所成的二面角的正切值。

剖析：由SA⊥面ABCD及不難發現，BC即為“第一垂線”，但是，本題要作二面角的平面角，還需首先作出二面角的棱．

略解2 延長BA、CD相交於點E，連結SE，則SE是所求二面角的棱，因為所以所以因為SA⊥面ABCD，得面SEB⊥面EBC，EB是交線，又所以BC⊥面SEB，故SB是CS在面SEB上的射影，所以所以∠BSC是所求二面角的平面角，因為，因為即所求二面角的正切值為．

2．藉助第三個平面，作“第一垂線”

例3 正三稜柱的底邊長為a，側棱長為，若經過對角線且與對角線平行的平面交上底面一邊於點D。

⑴確定點D的位置，並證明你的結論；

⑵求二面角的大小。

剖析：由線面平行的性質定理及三角形中位線性質，易知D是中點．二面角的放置屬於非常規位置的圖形，但是，容易發現，平面過點D且與平面垂直，這樣的平面相對於二面角的兩個平面而言，我們稱為第三個平面。過D作，由面面垂直的性質知，，即DF為我們要作的“第一垂線”。

略解2 在平面內，作於F，連DC，由三垂線定理可證∠DGF就是二面角的平面角，在正中，因為D是中點，，所以，在Rt△DFG，可求得

3．利用特殊圖形的定義、性質作“第一垂線”

例4 已知：Rt△ABC的斜邊BC在平面內，AB、AC分別與平面。成30°和45°角，求平面與△ABC所在平面所成二面角的大小。

剖析：本題中沒有相對於二面角的兩個平面的第三個平面可以藉助，但是，我們注意到AB、AC與平面所成的角均已給出，只要過A作AO⊥於O，就可以同時找到AB、AC在平面內的射影，無疑這樣得到的“第一垂線"AO有著非常特殊的位置，有利於二面角大小的計算。

解：作AO⊥於O，於D，連OB，AD，OC，由三垂線定理得：所以∠ADO是二面角A—BC—O的平面角，令在Rt△AOB中，所以在Rt△AOC中，

在Rt△AOD中，，所以所以三角形ABC與面成60°或120°的二面角。

空間圖形的位置關係是立體幾何的重要內容，解決立體幾何問題的關鍵在於三定：定性分析→定位作圖→定量計算，其中定性是定位、定量的基礎，而宣則是定位、定性的深化，在面面關係中，二面角是其中的重要概念之一，它的度量歸結為平面上角的度量，一般來說，對其平面角的定位是問題解決的先決一步，可是，從以往的教學中發現，學生往往把握不住其定位的基本思路而導致思維混亂，甚至錯誤地定其位，使問題的解決徒勞無益，本文就是針對這一點，來談一談平日教學中體會。

一、重溫二面角的平面角的定義

α、β是由ι出發的兩個平面，O是ι上任意一點，OC

α，且這就是二面角的平面角的環境背景，即∠COD是二面角的平面角，從中不難得到下列特徵：

Ⅰ、過棱上任意一點，其平面角是唯一的；

Ⅱ、其平面角所在平面與其兩個半平面均垂直；

另外，如果在OC上任取上一點A，作垂足為B，那麼

由特徵Ⅱ可知.突出ι、OC、OD、AB，這便是另一特徵；

Ⅲ、體現出一完整的垂線定理（或逆定理）的環境背景。

對以上特徵進行剖析

由於二面角的平面角是由一點和兩條射線構成，所以二面角的平面角的定位可化歸為“定點”或“定線（面）”的問題。

特徵Ⅰ表明，其平面角的定位可先在棱上取一“點”，耐人尋味的是這一點可以隨便取，但又總是不隨便取定的，它必須與問題背景相互溝通，給計算提供方便。

例1 已知正三稜錐V—ABC側棱長為a，高為b，求側面與底面所成的角的大小。

由於正三稜錐的頂點V在底面ABC上的射影H是底面的中心，所以連結CH交AB於O，且，則∠VOC為側面與底面所成二面角的平面角。正因為正三稜錐的特性，解決此問題，可以取AB的中點O為其平面角的頂點，而且使背景突出在面VOC上，給進一步定量創造得天獨厚的條件。

特徵Ⅱ指出，如果二面角的棱ι垂直某一平面γ與

α、β的交線，而交線所成的角就是的平面角。

由此可見，二面角的平面角的定位可以考慮找“垂平面”。

例2 矩形ABCD，沿對角線BD把△ABD折起，

使點A在平面BCD上的射影A′落在BC上，求二面角A—BC-—C的大小。

這是一道由平面圖形摺疊成立體圖形的問題，解決問題的關鍵在於搞清摺疊前後“變”與“不變”。結果在平面圖形中過A作交BD於O、交BC於E，則摺疊后OA、OE與BD的垂直關係不變。但OA與OE此時變成相交兩線段並確定一平面，此平面必與棱垂直。由特徵Ⅱ可知，面AOE與面ABD、面CBD的交線OA與OE所成的角，即為所求二面角的平面角。另外，A在面BCD上的射影必在OE所在的直線上，又題設射影落在BC上，所以E點就是A′，這樣的定位給下面的定量提供了優質服務。事實上，而tan∠CBD，故。在Rt△AA′O中，所以，即所求的二面。

通過對例2的定性分析、定位作圖和定量計算，特徵Ⅱ從另一角度告訴我們：要確定二面角的平面角，我們可以把構成二面角的兩個半平面“擺平”，然後，在棱上選取一適當的垂線段，即可確定其平面角。“平面圖形”與“立體圖形”相映生輝，不僅便於定性、定位，更利於定量。

特徵Ⅲ顯示，如果二面角α—ι—β的兩個半平面之一，存在垂線段AB，那麼過垂足B作ι的垂線交ι於O，連結AO，由三垂線定理可知；或者由A作ι的垂線交ι於O，連結OB，由三垂線定理逆定理可知此時，∠AOB就是二面角α—ι—β的平面角。

由此可見，地面角的平面角的定位可以找“垂線段”。

例3 在正方體中，棱長為2，E為BC的中點。求面所成的二面角的大小。

例3的環境背景表明，面構成兩個二面角，

由特徵Ⅱ可知，這兩個二面角的大小必定互補，下面，如

果思維由特徵Ⅲ監控，背景中的線段會使眼睛一亮，我們只須由作的垂線交於O，然後連結，即得面所成二面角的平面角計算可得

在中，。

故所求的二面角角為或

以上三個特徵提供的思路在解決具體總是時各具特色。

分別找“點”、“垂面”、“垂線段”。事實上，我們只要找到其中一個，另兩個就接踵而來。掌握這種關係對提高解題技能和培養空間想象力非常重要。

1、融合三個特徵對思維的監控，可有效地克服、抑制思維的

消極作用，培養思維的廣闊性和批判性。

例3 將棱長為a的正四面體的一個面與棱長為a的正四稜錐的

一個側面吻合，則吻合后的幾何呈現幾個面？

這是一道競賽題，考生答“7個面”的佔99.9%，少數應服從多數嗎？

過兩個幾何體的高線VP、VQ的垂足P、Q分別作BC的垂線，則垂足重合於O，且O為BC的中點，OP延長過A，OQ延長交ED於R。由特徵Ⅲ，∠AOR為二面角A—BC—R平面角，結合特徵Ⅰ、Ⅱ，可得VAOR為平行四邊形，所以V、A、B、E共面，同理V、A、C、D共面，所以這道題的答案應該是5個面！

2、三個特徵，雖然客觀存在，互相聯繫，但在許多同題中卻

表現得含糊而冷漠——三個“標的”均藏而不露，在這種形勢下，逼你去作，那麼作誰？

由特徵Ⅲ，有了“垂線段”便可定位。

例4 已知Rt△ABC的兩直角邊P為斜邊上一點，沿CP將此直角三角形折成直二面角A—CP—B，當時，求二面角P—AC—B的大小。

作法一：∵A—CP—B為直角二面角，

∴過B作交CP的延長線於D，則 APC。

∴過D作，垂足為E，連BE。

∴∠DEB為二面角A—CP—B的平面角。

作法二：過P點作交BC於D′，則

∴過D′作垂足為E′，邊PE′，

∴∠D′E′P為二面角P—AC—B的平面角。

再說，定位是為了定理，求角的大小往往要化歸到一個三角形中去解，有了“垂線段”就可把它化歸為解一個直角三角形。

由此可見，要作，最好考慮作“垂線段”。

綜上所述，二面角其平面角的正確而合理的定位，要在正確其定義的基礎上，掌握其三個基本特徵，並靈活運用它們考察問題的環境背景，建立良好的主觀心理空間和客觀心理空間，以不變應萬變。