共找到2條詞條名為橢圓曲線的結果 展開
- 平面上光滑的三次曲線
- 顏松遠所著書籍
橢圓曲線
平面上光滑的三次曲線
橢圓曲線是域上虧格為1的光滑射影曲線。對於特徵不等於2的域，它的仿射方程可以寫成：y^2=x^3+ax^2+bx+c。複數域上的橢圓曲線為虧格為1的黎曼面。Mordell證明了整體域上的橢圓曲線是有限生成交換群，這是著名的BSD猜想的前提條件。阿貝爾簇是橢圓曲線的高維推廣。
平面上光滑的三次曲線稱作橢圓曲線. 在一個合適的坐標系下，它的一般方程可寫作
，
這裡a,b等均為係數. 這樣的方程稱作Weierstrass方程
註：我們通常允許x,y取複數, 因此這樣的曲線實際上是複數坐標點所描繪的軌跡。但為了形象說明, 通常的圖形仍然以實數坐標來描繪。
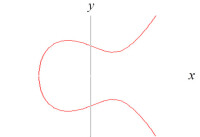
橢圓曲線在實坐標里的圖形
在合適的坐標變換下, 橢圓曲線可以寫成如下各類形式的標準方程。
(Weierstrass標準型)
(Legendre形式)
(Deuring形式)
考慮Weierstrass標準方程.我們定義
它稱為橢圓曲線的j不變數.
橢圓曲線的j不變數唯一確定橢圓曲線。換言之, 如果E,E'是兩條橢圓曲線, 那麼E和E'同構當且僅當它們有相同的j不變數.
橢圓曲線也可以退化成一些非光滑情形:
1. 帶尖點的有理曲線，比如.
尖點曲線在實空間中的圖形
結點曲線在實空間中的圖形
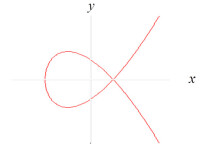
帶結點的有理曲線
3. 一條圓錐曲線和一條直線的並集.
4. 三條直線的並集.
由於我們考慮的橢圓曲線坐標點(x,y)允許取複數作為分量，所以它實際上是復二維平面內的圖形. 將x,y分別寫成實部與虛部的形式，復二維平面相當於實數域上的四維空間。
此時，橢圓曲線方程變成了兩個代數方程的公共零點集--有四個實數變數。因此橢圓曲線就變成了四維空間中的一個二維圖形。利用拓撲學或複變函數的方法，我們可以看到，這樣的圖形就是通常的環面--即虧格1閉曲面。
環面
註：環面可以通過粘合正方形的兩對對邊得到。
橢圓曲線所描繪的圖形並非橢圓。其名稱含“橢圓”二字是因為它和橢圓積分有關。
這裡sqrt是指開根運算。等式兩邊平方即得橢圓曲線方程。
橢圓積分是不能用初等函數寫出其表達式的。
一條曲線的切線和這條曲線相切的程度可以用如下方式來看：稍微擾動該切線，則該線與曲線的原切點變成了若干個相交點，這樣的交點的個數稱作切線與該曲線在切點除的相交數。相交數也可以理解為將切點看成若干個交點重合在一起。
切線在切點處的相交數至少是2. 如果該相交數至少是3，我們就說，這個切點是該曲線的拐點。
橢圓曲線上共有9個拐點。為方便討論，我們通常將其中一個拐點放到無窮遠處--以下都默認這種情形。
(1) （Bezout定理特例）兩條光滑橢圓曲線相交9個點（切點重複計算，見上）。
一條橢圓曲線和一條圓錐曲線相交6個點。
一條橢圓曲線和一條直線相交3個點。
(2) （Chaseles定理）如果有第三條光滑橢圓曲線經過兩條光滑橢圓曲線的其中8個交點，那它必定經過第九個點。
(3) 存在12條直線經過橢圓曲線的9個拐點，並且每條直線恰好經過其中三個拐點。
註：將橢圓曲線退化情形放到上述各結論中，我們能到了射影幾何中的許許多多著名定理，比如帕斯卡定理等等。
我們假設點O是橢圓曲線C的拐點，設P,Q是橢圓曲線上任何兩點. 設L是連接PQ的直線（如果, 則L就是切線）. L與橢圓曲線C相交第三個點, 記作. 設H是連接O與P*Q的直線, 那麼H與C相交另一點, 記作.
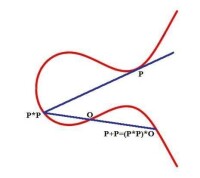
橢圓曲線加法運算（P=Q情形)
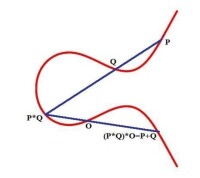
橢圓曲線的加法運算
"+"定義了橢圓曲線上點與點之間的加法運算,。這一運算滿足群的性質：
(1) 零元：
(2) 結合律：
(3) 逆元: 存在唯一的點(-P), 使得.
進一步, 我們有
(4) 交換律:.
這樣,構成了加法群。正因為橢圓曲線存在加法群結構，所以它包含了很多重要的數論信息。這是一般的曲線所沒有的特殊性質。
註：橢圓曲線和它的雅可比簇是同構的，所以它上面的“加法”結構實際上來自於它的雅可比簇的自然加法結構。
在橢圓曲線上, 我們取定拐點后, 如上方法得到一個群結構. 設P是其中一點。如果P和自身相加若干倍后等於O, 我們就說P是撓點. 假設n是最小的正整數, 使得(即n個P相加等於零元), 我們稱P是n階撓元.
橢圓曲線上有個n階撓元. 更精確地, 所有n階撓元都可以由兩個n階撓元生成, 即有如下形狀 (這裡P,Q是n階撓元, a,b取整數).
橢圓曲線的撓元包含了橢圓曲線大量的重要信息。
假設橢圓曲線C的Weierstrass定義方程的係數都是有理數。我們關心橢圓曲線上的所有的有理點構成的集合, 記作C(Q). 所謂有理點就是指(x,y)中的分量x和y都是有理數的點。
(Modell定理) C(Q)是的子群, 它是有限秩的. 換言之,
這裡表示r個整數加法群Z的直和,指有理撓點構成的子群。
(Mazur定理) 必是以下情形之一:
(1) 或,
(2), .
這裡是指同餘k下的剩餘類加法群.
註：人們至今尚未研究清楚C(Q)無撓部分的秩r，它和許多重要的難題與猜想有關，比如著名的BSD猜想。
設P,Q是橢圓曲線上的有理點，那麼很容易看到也是有理點。這就提供了一個從已知有理點構造出新的有理點的方法。
橢圓曲線的有理點問題與許多數論方程有關。
在退化情形,
(1) 著名的勾股方程就相當於求單位圓周的有理點。
(3)著名的二次剩餘問題，相當於求拋物線上的整點.
因此人們很自然會去尋求橢圓曲線上的有理點和整點。
（1）
是費馬猜想中的一個方程. 該方程由高斯和歐拉分別解決. 費馬利用以下初等變換, 將該方程歸結為橢圓曲線的有理點計算。
將上式代入費馬方程即得
因為此方程已知無非平凡解, 所以這相當於上述有理曲線僅有兩個有理點和.
（2）
由費馬利用無窮遞降法證明無平凡解。它也可以通過以下初等變換變成橢圓曲線：
,
代入原方程即得
.
它僅有三個有理點.
（3）, n是素數
假設是一組非平凡解。此時人們構造了橢圓曲線
這條橢圓曲線稱作Frey曲線。Ribet 1968年證明該曲線不能是模曲線. 而另一方面Wiles 於1995年證明Taniyama-Shimura猜想, 即任何橢圓曲線都是模曲線，這就等於證明費馬方程無非平凡解。
（同餘數問題）給定正整數n, 是否存在直角三角形，使得三條邊都是有理數, 並且面積恰好是n? 如果存在這樣的三角形, 就稱n是同餘數. 比如不是同餘數，是同餘數.
這一問題等價於求解正有理數(a,b,c)滿足:
.
令
則得
因此問題就歸結為求上述橢圓曲線的有理點.
基本信息
- 中文名
- 橢圓曲線
- 外文名
- elliptic curve
- 定義
- 平面上光滑的三次曲線稱作橢圓曲線
- 適用範圍
- 數理科學
- 模性
- 整體域上橢圓曲線的L函數等於某一個自守形式的L函數
- 解釋
- 域上虧格為1的光滑射影曲線