格拉斯曼
德國數學家、語言學家
格拉斯曼(1809～1877)
Grassmann，Hermann Gunther
格拉斯曼
格拉斯曼，H．G．（Grassmann，Hermann Günther) 1809年4月15日生於德國波美拉尼亞的斯德丁（今波蘭什切青）；1877年9月26日卒於斯德丁．數學．
格拉斯曼出生於一個知識分子家庭，父親賈斯特斯（Justus）研究過神學、數學和物理學．母親J．美登沃爾德（Medenwald）是一位牧師的女兒．在他們家的12個孩子中，格拉斯曼排行第三．他40歲才結婚，妻子M．T．納普（Knappe）是一個地主的女兒，生有11個孩子，其中盧多爾夫（Ludolf）成為物理學家，赫爾曼（Hermann）成為數學家，其他人也多有成就．
格拉斯曼最初的教育來自母親和一所私立學校．18歲時他通過了中等學校的最後考試，隨後與他的長兄古斯塔夫（Gustav）一起在柏林大學學了三年神學和古典語言文學．
1830年秋，格拉斯曼回到斯德丁，開始自學數學和物理．1832年在斯德丁得到一個大學預科助教的職位． 1834年通過斯德丁的教會代表會議主持的第一級神學考試，這年秋天到柏林的格沃貝舒里學校當副校長，1835年又被派到斯德丁新成立的奧托學校任教．他教過數學、物理、德語、拉丁語和宗教等課程．同時，在任教期間仍進行神學、數學和自然科學等方面的研究．1839年，他在斯德丁通過了第二級神學考試．次年又在柏林通過了數學、物理、化學和礦物學方面的考試，從而取得了擔任中等學校各級教學工作的資格．此後，格拉斯曼在教學上花了較大的精力，編寫了幾本中學課本．1852年，他接替父親的工作，在斯德丁大學預科做了四級教師，這是一個可以獲得教授頭銜的職位．
格拉斯曼興趣廣泛，多才多藝，早在青年時期就在多方面取得成績．1846年，他的《解析幾何》（Geometrische，Analyse）得到公眾好評，並獲得萊比錫科學協會的最高獎賞．1845年，他出版了《電動力學理論》（Neue Theorie der Elektrodynamik），書中以新的定律取代了安培關於兩個極小的電流元件相互作用的基本定律．1853年又發表文章“混色理論”（Zur Theorie der Farben－mischung）．1864年，他因物理方面的成績被選為利奧波德學會會員．另外，他還是梵文權威，也曾努力學習過哥德語、立陶宛語、古波斯語、俄語和教會斯拉夫語，並在此基礎上研究比較語言學．1860年，他開始對吠陀經典讚美詩進行深入研究，此書至今仍在廣泛應用。1876—1877年間，他又寫成讚美詩的德文譯本．他的這些成績得到學術界的好評，很快為學者們所接受，使他在1876年成了美國東方學會的成員．蒂賓根大學哲學系授予他名譽博士學位．
格拉斯曼的數學成就遠遠走在他那個時代的前面．他是一位自學成材的數學家，1832年就開始了一種新的幾何演演演算法的研究．他意識到自己工作的深遠意義，到1840年已把全部精力集中到數學方面的研究．1843年秋，他完成了名著《線性擴張論》（Die lineare Ausaenuangslehre）的第1卷，於1844年發表．可惜的是它的基本意義沒有被當時人們所領會，因為其內容實在比當時的數學水平深得多，而且敘述抽象，在文中還夾雜著哲學理論和神秘的教義．1845年以後他又寫了很多書和文章，將他的理論應用到物理及代數曲線和曲面上，但也沒有獲得人們的理解．於是他把《線性擴張論》修改加工，更名《擴張論》（Die Ausaenuang－slehre），於1862年在柏林出版．但此書還是沒有用具體明確的例子說明他的新概念，仍然十分難懂，沒有受到學術界重視．連續幾次失敗使他失望，53歲以後逐漸離開數學，專門研究梵文．
直到格拉斯曼晚年的時候，人們才注意到他的數學著作的價值．1871年，他被選為哥丁根科學院的通訊會員．這時他已年老體弱，但一直堅持工作．在他去世后，專家們努力把他的《擴張論》向數學界介紹，還有人為他寫了傳記，在他一百歲誕辰時出版了他的論著全集．
格拉斯曼在數學上的主要貢獻表現在他對多維空間的研究．多維空間產生的原因之一，是在解決代數和分析的問題時試圖利用幾何方法．當時已有用幾何方法解決純代數問題的先例．但是如果未知數多於三個，三維空間就不夠用了。為了保留有效的幾何思想方法，就需要引入抽象的n維空間概念。這種空間的點由n個坐標決定，從而把在三個變數時起作用的幾何方法應用到任意個變數的情形．
在解析幾何與綜合幾何的基礎上，G．W．萊布尼茲(Leibniz）曾設想過這種幾何分析，但他沒有深入闡述自己的觀點．格拉斯曼首次提出了多維歐幾里得空間的系統理論．1844年他在《線性擴張論》中引入歐幾里得n維空間概念，研究了點、直線、平面和兩點間的距離，並推廣到n維空間，研究了抽象幾何空間中的n階曲線，發展了萊布尼茲把代表幾何實體的符號按一定規則來處理的代數思想．
《線性擴張論》所論述的幾何分析，是一個介於解析幾何與綜合幾何的邊緣領域．幾何分析的所有體系具有共同特點，它們的基本成分是有向線段的幾何加法，並且藉助於複數的平面幾何描述．在《線性擴張論》中格拉斯曼融合坐標、向量及複數等概念於n維空間，大膽地開拓了數學的新領域．
“向量空間”概念在以前數學家的論著中是不夠明確的，格拉斯曼第一個明白地解釋了“n維向量空間”的概念，他把n維向量空間的向量和與積用純幾何方法來定義，發展了通用的向量演演演算法．
格拉斯曼與W．R．哈密頓（Hamilton）同時分別建立了超複數，格拉斯曼還引入了超複數的兩類乘法（內積和外積），從而建立了一種有n個分量的超複數幾何學，所以他是復抽象幾何學的奠基人． 由於坐標選擇帶有任意性，可能使問題複雜化．人們希望把幾何學和物理學上確實重要的部分，與由坐標的選擇額外產生的部分分開，於是便產生了張量概念．用張量來描述的物理定律和幾何定理所得到的結果，在任何坐標系下都具有不變的形式．
這是一種有n個分量的趨複數，下面用n=3的情況為例來說明他的思想．設兩個超複數α=α1e1+α2e2+α3e3，β=β1e1
格拉斯曼
格拉斯曼
格拉斯曼
間的夾角，則 (a，b分別是α，β的線向量）．對超複數的外積P，他假設[eiej]=-[ejei]=eij(1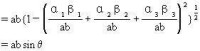
所以|P|就是一個平行四邊形的面積．如果兩個向量位於同一直線，則它們的積是0；否則它們張成一個位於某一平面並有一確定面積的平行四邊形．
P=[αβ]=（α2β3-α3β2)[e2e3]+（α3β1-α1β3)[e3e1]+（α1β2-α2β1)[e1e2]，
且有αβ=-βα．
格拉斯曼
對兩個積ab和cd相等，格拉斯曼解釋為：它們位於平行平面之中，張成的面積相同，並且從c到d和從a到b有相同的旋向．至於三個向量的積，則可構成一個有向平行六面體．他還考慮了高階乘積．1855年又對超複數給出了16種不同類型的乘積及其幾何意義．並在力學、磁學、晶體學等方面作了應用．
與格拉斯曼幾乎同時而獨立地用分析方法研究n維幾何的，還有A．凱利（Cayley）和G．黎曼（Riemann），他們都是通過與普通解析幾何作形式類比而進行的，但影響不及格拉斯曼．雖然他的n維超複數分析終究未建立起來（因為沒有發現這種分析的應用），但他的思想引導數學家進入張量理論．張量的引入，使數學家們既採用坐標又擺脫具體坐標系的影響，使推導簡化，而且能充分反映事物的屬性．它在力學、幾何學、電磁場及相對論等方面有著廣泛的應用．20世紀80年代歐美國家掀起了學習和應用張量的熱潮．中國隨著計算數學、應用數學的發展，張量理論也受到很多專家的重視． J．吉布斯（Gibbs）和O．希維賽德（Heavislde）創立向量代數，也受到格拉斯曼的很大影響．向量代數可以從格拉斯曼和哈密頓的概念中導出，吉布斯曾說過他更喜歡格拉斯曼的限制較少的概念．格拉斯曼的著作還影響著線性矩陣代數的誕生，在其著作中已有這方面知識的萌芽．1862年，格拉斯曼提出了矩陣化成三角式的方法，並論述了這種方法與射影變換之間的關係．
在代數方面，格拉斯曼的工作遠遠超過了哈密頓的四元數，他不只考慮實數有序四元數組，而且考慮實數有序n元數組．格拉斯曼還發展了一項他稱為“代數的”乘法，它遵守定律eiej=ejei，i=1，…，n，並導致了今天的多項式環．格拉斯曼和哈密頓、凱利等數學家是近世代數的先驅，他們推出了不同於普通代數的、遵守某種結構規律的代數方法，具有深遠的意義．就象羅巴切夫斯基（ЛoбaЧeBCKИй）的發現導致幾何的解放一樣，格拉斯曼的工作導致了代數的解放，打開了現代抽象代數的大門．格拉斯曼的分析研究還涉及
積分理論的積分理論．他提出了一個重要定理：如果把k視為ω類——就是說，ω可以變換成交量的極小數量——那麼，當k=2h時，ω可變換成為範式Zn+1dZ1+…+Z2ndZn，而當k=2h-1時，則可變換成P·（dZh+Zh+1dZ1+…+Z2h-1dZh-1），這裡的P是Z1…Z2h-1的函數．
格拉斯曼還研究了算術基礎，他在《算術教本》（Lehrbuchder Arithmetik，1861）中對算術基礎作了科學論證，給出自然數加法和乘法的定義，並證明了加法和乘法的基本性質，如交換律、結合律、分配律等．他的研究以（a+b)+1=a+(b+1）為依據．
由於格拉斯曼的貢獻，很多數學名詞以他的名字命名，如格拉斯曼坐標、格拉斯曼錐體、格拉斯曼平麵線性生成等等．他還首創了以坐標表示給定空間的子空間的方法，從而導致了稱為格拉斯曼代數流形的映射點．
基本信息
- 中文名
- 格拉斯曼
- 外文名
- Grassmann
- 國籍
- 德國
- 出生地
- 普魯士波美拉尼亞省的海港城市斯德丁
- 出生日期
- 1809-04
- 去世日期
- 1877-09
目錄