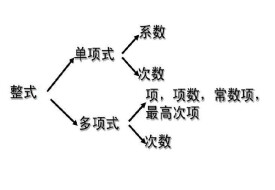
整式

單項式與多項式統稱為整式。

例題：

、、是整式。不是整式。

由數與字母的積或字母與字母的積所組成的代數式叫做單項式（monomial）。單獨一個數或一個字母也是單項式，如Q，-1，a，β等。

係數：

（1）單項式中的常數因數叫做單項式的係數（coefficient），如3x的係數是3。

（2）如果一個單項式只含有字母因數，是正數的單項式係數為1，是負數的單項式係數為-1，如係數為1。係數為-1。

（3）如果只是一個數字，係數是本身。如5的係數還是5。

次數：

一個單項式中，所有字母指數的和叫做這個單項式的次數（degree of a monomial）。例如中字母x的次數是1，字母y的次數是2，則的次數為1+2=3，又如，次數為，因為3的次數3不算入單項式的次數中。

單獨一個非零數的次數是0。

易錯混點：

（1）單項式的係數包括前面的符號，如：-a的係數是-1；

（2）單項式是由數字因數和字母因數組成的，單項式不含加減運算，含有除法運算時，分母不含字母，分子不含加減運算，如：就不是單項式，也不是單項式，因為它們都含加減運算（但第二題也不是分式，因為是一個數，所以它是多項式）；

（3）單項式的次數與多項式的次數是不同概念，要注意區分；

（4）係數是1或-1時，省略1不寫；指數是1時，1也省略不寫，在這兩個知識點上容易出現錯誤。

加減法則：

單項式加減即合併同類項，也就是合併前各同類項係數的和，字母不變。

例如：,等。

同時還要運用到去括弧法則和添括弧法則。

乘法法則：

單項式相乘，把它們的係數、相同字母分別相乘，對於只在一個單項式里含有的字母，則連同它的指數作為積的一個因式

例如：

除法法則：

同底數冪（次方）相除，底數不變，指數相減。

由有限個單項式的代數和組成的代數式叫做多項式（polynomial）。（化為最簡式，即（常數）（指數不為負數））

項：在多項式中，每個單項式叫做多項式的項，其中不含字母的項叫做常數項。一個多項式合併同類項後有幾項就叫做幾項式。多項式中的符號，看作各項的性質符號。一元N次多項式最多N+1項。

例：在多項式中，和-3是它的項，其中-3是常數項；在多項式中它的項分別是、和18，其中18是常數項，它是三項式。

次數：多項式中，次數最高的項的次數，就是這個多項式的次數，如：中，這一項的次數最高，這個多項式的次數就是，這個多項式就是八次三項式。

排列：有時為了計算需要，可以將多項式各項的位置根據加法交換律按照其中某個字母的指數大小順序來排列。

例如：把多項式 按字母x指數從大到小的順序排列，寫成 ，這叫做把多項式按字母x的降冪排列，若按x指數從小到大排列，則就是把多項式按字母x的升冪排列，寫成 ，也可以是多項式中的其他字母。

易錯混點：

（1）多項式的次數是次數最高項的次數，而不是各項次數的和，應理解透概念。

（2）看清是降冪還是升冪排列。

（3）降冪和升冪排列都是以某一個字母（未知量）來排序。

就是單項式和多項式的加減，可利用去括弧法則和合併同類項來完成。

例如，

1. 整數指數律(Laws of Indices)

同底數冪的乘法

底數是相同的冪即為同底數冪。

同底數冪相乘，底數不變，指數相加。

即，（m，n為正整數），如

冪的乘方

冪的乘方，底數不變，指數相乘。

即（m，n為正整數），如

積的乘方

積的乘方，先把積中的每一個因數分別乘方，再把所得的冪相乘。

用字母表示為：（n為正整數），如

2. 多項式乘法 (Multiplication of Polynomials)

單項式與單項式相乘

單項式與單項式相乘，把它們的係數、同底數冪分別相乘，對於只在一個單項式里含有的字母，則連同它的指數作為積的一個因式。

例如：

單項式與多項式相乘

單項式與多項式相乘，就是用單項式去乘多項式的每一項，再把所得的積相加。

例如：

多項式與多項式相乘

多項式與多項式相乘，先用一個多項式的每一項乘另一個多項式的每一項，再把所得的積相加。

例如：

乘法公式（Identities）：也叫做簡乘公式，就是把一些特殊的多項式相乘的結果加以總結，直接應用。公式中的每一個字母，一般可以表示數字，單項式，多項式，有的還可以推廣到分式，根式。

常用公式：

完全平方公式：

三數和平方公式：

平方差公式：

立方和公式：

立方差公式：

完全立方公式：

歐拉公式：

二項式定理：

和的展開式：

因式分解（Factorization）：把一個多項式化為幾個最簡整式的乘積的形式，這種變形叫做把這個多項式因式分解（也叫作分解因式）。分解因式與整式乘法為相反變形。

因式分解沒有普遍適用的法則，初中數學教材中主要介紹了提公因式法、公式法、分組分解法、十字相乘法、配方法、待定係數法、拆項法等方法。

提公因式法（Take out Common Factor）：又叫提取公因式法。

一個多項式中每一項都含有的因式叫做這個多項式的公因式。

如果多項式的各項有公因式，可以把這個公因式提取出來作為多項式的一個因式，提取公因式后的式子放在括弧里，作為另一個因式，這種因式分解的方法叫提公因式法。

例如，公因式為，因式分解結果為。

公式法(Using Identities)：逆用乘法公式將一個多項式分解因式的方法叫公式法。

因式分解常用乘法公式：

因式分解中的平方差公式：

因式分解中的完全平方公式：

因式分解中的三數完全平方公式：

十字相乘法(Cross Method)：運用十字交叉線來分解係數，把二次三項式分解因式的方法叫十字相乘法。

如果二次三項式中的常數項能分解成兩個因數的積，而且一次項係數又恰好是，那麼就可進行以下的因式分解：

完全平方式也可用此公式分解。

例如，

分組分解法(Grouping Method)：

利用分組來分解因式的方法叫分組分解法。

若是四項式，一般二二分組或一三分組。

例如，是一三分組。

同底數冪的除法

同底數冪相除，底數不變，指數相減。

（m、n是正整數且）

例如，

任何不等於零的數的零次冪為1，即

單項式除以單項式

單項式相除，把係數、同底數冪分別相除后，作為商的因式；對於只在被除式中含有的字母，則連同它的指數一起作為商的一個因式。

註：單項式除以單項式主要是通過轉化為同底數冪的除法解決的。

例如，

多項式除以單項式

多項式除以單項式，先把多項式的每一項分別除以這個單項式，再把所得的商相加。

例如，

題型

若按某個字母的指數從—的順序排列，叫做這個多項式按這個字母降冪排列。