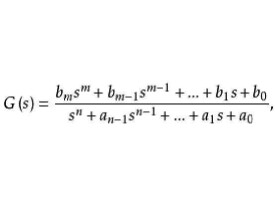單輸入單輸出系統
單輸入單輸出系統
單輸入單輸出系統(SISO)也稱為單變數系統,系統的輸入量與輸出量各為一個。經典控制理論主要就是研究這一類系統。多輸入多輸出系統(MIMO)也稱為多變數系統,系統的輸入量與輸出量多於一個。現代控制理論適用於這類系統的分析與綜合。其數學工具為建立在線性代數基礎上的狀態空間法,這種方法是在時間域內進行的,而時域分析法對控制過程來說是最直接的。
若系統只有一個輸入和一個輸出,則這個系統為 單輸入-單輸出系統或 單變數系統。有兩個以上輸入或兩個以上輸出,則為 多輸入-多輸出系統或 多變數系統。
為了導出單輸入單輸出系統的數學關係,設初始時刻,假定系統的輸出 僅由輸入 唯一確定,即給定了一個 就唯一確定了系統的輸出,稱系統初始具有 鬆弛性。
如果所討論的系統是物理系統,當系統在 時不儲有能量,則容易看出,系統輸出完全由外部輸入唯一確定,即系統初始具有鬆弛性。例如,對於電阻、電容、電感構成的電網路,在初始時刻,若電容的端電壓為零,電感中的電流也為零時,電網路的初始能量為零,即電網路初始具有鬆弛性。
如對上式進行拉氏變換,若初值為零,則其傳遞函數為
即為系統的傳遞函數。
傳遞函數分子多項式的零點,稱為系統的零點;分母多項式即為系統的特徵多項式,分母多項式的零點(特徵根)稱為系統的極點;特徵多項式的次數,稱為系統的維數(或階數)。
由系統的高階微分方程的描述也很容易得到系統的傳遞函數。
對於線性定常單輸入單輸出系統,有如下一些結論。
(1)單輸入單輸出系統 既能控又能觀的充要條件是其傳遞函數g(s)不存在零極點相消現象。
由於非奇異變換不改變系統的傳遞函數,因此,可以僅討論傳遞函數的特徵值規範型實現。於是,上述結論可以說明如下:
先討論對角線規範型的情況,這時有
式中,為系統的互不相同的特徵值。
系統對應的傳遞函數為
根據對角線規範型能控、能觀性判據,系統既能控又能觀的充要條件是 和 都不為0,這意味著傳遞函數g(s)不存在零極點相消現象,因為當傳遞函數g(s)存在零極點相消現象時,被消極點 對應的。
再討論約當規範型的情況。為討論方便,這裡具體地設定為3重特徵值,即
它對應的傳遞函數是
由約當規範型能控、能觀性判據,系統既能控又能觀的充要條件是,這同樣意味著傳遞函數g(s)不存在零極點相消現象,因為當傳遞函數g(s)存在零極點相消現象時,必有。
(2)單輸入系統狀態完全能控的充要條件是由控制到狀態的傳遞關係 不存在零極點相消現象。
對於對角線規範型(1)的情況,由控制到狀態的傳遞關係是
根據對角線規範型能控性判據,系統狀態完全能控的充要條件是,這意味著由控制到狀態的傳遞關係 不存在零極點相消現象。因為由式(3)可知,當傳遞關係 存在零極點相消現象時,被消極點 對應的。
對於約當規範型(2)的情況,由控制到狀態的傳遞關係是
由約當規範型能控性判據,系統狀態完全能控的充要條件是,這同樣意味著由控制到狀態的傳遞關係 不存在零極點相消現象。因為由式(4)可知,當 存在零極點相消現象時,必有。
(3)單輸出系統狀態完全能觀的充要條件是由狀態到輸出的傳遞關係 不存在零極點相消現象。
這一結論可由結論(2)的對偶關係得出。
(4)單輸入單輸出系統 既不能控又不能觀的充分條件是其預解矩陣 存在零極點相消現象。
該結論也可以用與上面類似的方法給以說明,這裡不再詳述。
控制理論是研究系統控制和動態一般規律的學科,動態指系統的行為隨時間而變化的現象,常用一些適當的作為時間函數的變數來描述。
早期的控制理論多是研究單輸入、單輸出的線路系統,關心的問題主要是穩定性、響應速度、頻率特性等問題。20世紀50年代末以後,注意力轉向多輸入、多輸出系統(線性的或非線性的)的研究,理論上取得很大進展,這些成果稱為現代控制理論,而將早期的理論稱為古典控制理論。現代控制理論還可用來描述一般複雜系統,為系統理論提供理論基礎。
控制理論不直接研究現實的具體系統,而是用數學方法討論幾類典型系統的模型。因此,應用控制理論的結果不受系統物理特性的局限。
控制理論是一門有廣泛應用和重大實用價值的理論。是研究在一定限制條件下如何控制系統以實現預期目標的一門理論。控制是用來影響動態系統行為的一種手段,對系統的控制是根據對其輸出的實際觀測所做出的決策再由輸入的作用來實現的,目的是使系統實現穩定和預期目標的運動。控制理論屬於技術科學範疇,可區分為基礎研究和應用研究兩個層次。在基礎研究層次中,強調採用精確的數學語言來闡述控制的特性和原理,最終從數學上建立分析和設計控制系統的理論和方法。在應用研究的層次中,著重於建立控制系統的工程化分析和設計方法,將控制規律轉化為可在計算機上實現的控制演演算法和相應的軟體,以及針對實際控制系統的具體特點採用控制理論的概念和方法解決實際問題。
控制理論的最早研究可追溯到1932年奈奎斯特(Nyquist,H.)對反饋放大器穩定性的分析。他在其著名的論文中提出了一種以系統頻率響應形式表達的判據,可用於判定反饋控制系統是否穩定,以及如何通過修正系統的特性使反饋系統由不穩定變為穩定或改善其穩定度.1940年,伯德(Bode,H.W.)進一步引入了可使頻率響應特性的運算和作圖簡化的對數增益圖和線性相位圖.1948年,埃文斯(Evans,W.R.)提出了根軌跡法,使以復變數理論為基礎的分析和設計反饋控制系統的方法更趨成熟。與此同時,維納(Wiener,N.)和柯爾莫哥洛夫(Колмогоров,А.Н.)於1940年分別提出了基於頻率域分析的信號處理的濾波和預測方法,它和建立在奈奎斯特穩定判據與埃文斯根軌跡法基礎上的控制理論一起形成了經典控制理論。1948年,維納嘗試把以工程問題為背景的經典控制理論的概念、原理和方法擴展到研究生物機理和神經系統,他的專著《控制論,或關於動物和機器中控制與通信的科學》標誌著一門獨立學科“控制論”的誕生.1954年,錢學森的專著《工程式控制制論》問世,成為控制論發展的又一個里程碑。經典控制理論的主要研究內容包括:單輸入-單輸出線性定常系統的預測、濾波和估計的原理和方法;單輸入-單輸出線性定常系統的穩定性、調節和補償的原理和方法;特殊單輸入-單輸出線性系統的快速控制的原理和實現方法等。
20世紀50年代,貝爾曼(Bellman,R.)在研究動態規劃中提出了“最優性原理——最優過程的任何最後一段都是最優的”,成為最優過程應當滿足的必要條件。緊接著,龐特里亞金(Понтрягин,Л.С.)等人提出了作為最優控制問題基本原理的“最大值原理”。最大值原理從另一角度建立了最優控制應滿足的必要條件,並從理論上完全解決了線性多變數系統的快速控制問題.20世紀60年代初,卡爾曼(Kalman,R.E.)將狀態空間方法系統地引入到控制系統的研究中,提出了揭示控制系統結構特性的兩個基本概念“能控性”和“能觀測性”。卡爾曼並和布西(Bucy,R.S.)一道,建立了基於時間域分析的新的預測、估計和濾波理論——卡爾曼濾波理論,這些概念、方法和理論的出現,標誌著控制理論進入了現代控制理論的新階段。隨著現代控制理論的發展,相繼形成了多個獨立的分支,如系統建模與系統辨識、線性系統理論、最優控制理論、魯棒控制理論、分佈參數系統理論、微分對策、適應控制以及非線性控制系統理論等。
控制理論是在重大工程問題的需求推動下形成和發展起來的。經典控制理論的形成和發展受到了通信技術和火炮技術的深刻影響,現代控制理論則是在遠程火箭技術與航天技術的推動下並受到電子計算機技術的促進而發展形成的。現今,現代控制理論的方法、概念和原理正在日益滲透到非工程系統領域,諸如社會經濟系統、生物和生態環境系統、現代管理系統以及集工程和管理為一體的更為複雜的系統。這類複雜系統的基本特徵,一方面表現為系統本身所在環境和運行機制的不完全確知性,另一方面表現在運行過程中總是包含有人的參與。對於這類複雜系統,目前已經發展了一些有效的控制方式,如分散控制方式,把計算機作為一個環節直接進入系統運行過程的控制方式,以及人的經驗和行為直接參與系統運行過程的控制方式等。但是,針對這類複雜系統的更為一般的分析、控制和綜合理論還遠未形成。