正交坐標

在數學里，一個正交坐標系定義為一組正交坐標 ，其坐標曲面都以直角相交。坐標曲面定義為坐標的等值曲面，或等值超曲面。例如，三維直角坐標是一種正交坐標，它的 x為常數，y為常數， z為常數的坐標曲面，都是互相以直角相交的平面，都互相垂直。

正交坐標時常用來解析一些出現於量子力學、流體動力學、電動力學、熱力學等等的偏微分方程。舉例而言，選擇一個恰當的的正交坐標來解析氫離子的波函數或消防水管的噴水，也許會比用直角坐標方便的多。這主要是因為恰當的正交坐標能夠與一個問題的對稱性相配合，從而促使應用分離變數法來成功的解析關於這問題的方程式。分離變數法是一種數學技巧，專門用來將一個複雜的n維問題變為n個一維問題。很多問題都可以簡化為拉普拉斯方程或亥姆霍茲方程，這些方程式可以用很多種正交坐標來分離。

在數學里，存在有各種各樣無限多的正交坐標系。應用二維直角坐標系(x,y)的共形映射方法，可以簡易的生成這些正交坐標系。一個複數的任何全純函數，其復值的導數，如果不等於零，則會造成一個共形映射。

如果可以表達為，則u與v的等值曲線以直角相交，就好似原本的x與y的等值曲線以直角相交。

三維與更高維的正交坐標系可以由一個二維正交坐標系生成，只要將二維正交坐標往一個新的坐標軸投射（形成類似圓柱坐標系的坐標系），或者將二維正交坐標繞著其對稱軸旋轉。可是，也有一些三維正交坐標系，例如橢球坐標系，則不能夠用上述方法得到。用數學術語，正交坐標的度規張量絕對沒有非對角項目。換句話說，無窮小距離的平方，可以寫為無窮小坐標位移的平方和： ；其中，n是維數，標度因子是度規張量的對角元素的平方根： ，這些標度因子可以用來計算一個正交坐標系的微分運算元。例如，梯度、拉普拉斯運算元、散度或旋度。

在數學里，笛卡兒坐標系（Cartesian坐標系），也稱直角坐標系，是一種正交坐標系。二維的直角坐標系是由兩條相互垂直、0 點重合的數軸構成的。在平面內，任何一點的坐標是根據數軸上對應的點的坐標設定的。在平面內，任何一點與坐標的對應關係，類似於數軸上點與坐標的對應關係。

採用直角坐標，幾何形狀可以用代數公式明確的表達出來。幾何形狀的每一個點的直角坐標必須遵守這代數公式。

通常兩個坐標軸只要互相垂直，其指向何方對於分析問題是沒有影響的，但習慣性地，x-軸被水平擺放，稱為橫軸，通常指向右方；y-軸被豎直擺放而稱為縱軸，通常指向上方。兩個坐標軸這樣的位置關係，稱為二維的右手坐標系，或右手系。如果把這個右手系畫在一張透明紙片上，則在平面內無論怎樣旋轉它，所得到的都叫做右手系；但如果把紙片翻轉，其背面看到的坐標系則稱為“左手系”。這和照鏡子時左右對掉的性質有關。

為了要知道坐標軸的任何一點，離原點的距離。假設，我們可以刻畫數值於坐標軸。那麼，從原點開始，往坐標軸所指的方向，每隔一個單位長度，就刻畫數值於坐標軸。這數值是 刻畫的次數，也是離原點的正值整數距離；同樣地，背著坐標軸所指的方向，我們也可以刻畫出 離原點的負值整數距離。稱 x-軸刻畫的數值為 x-坐標，又稱橫坐標，稱 y-軸刻畫的數值為 y-坐標，又稱縱坐標。

直角坐標系也可以推廣至三維空間與高維空間 (higher dimension)。

直角坐標系的 x-軸與 y-軸必須相互垂直。稱包含 y-軸的直線為 y-線。在二維空間里，當我們設定了 x-軸的位置與方向的同時，我們也設定了 y-線的方向。通常，我們選擇的取向是，正值的 x-軸橫地指向右方，正值的 y-軸縱地指向上方。這種取向稱為正值取向，標準取向，或右手取向。

右手定則是一種常用的記憶方法，專門用來辨認正值取向：將一隻半握拳的右手放在平面上，大拇指往上指，那麼，其它的手指都從 x-軸指向 y-軸。另外一種取向，採用左手定則，專門用來辨認負值取向，或左手取向：將一隻半握拳的左手放在 xy-平面上，大拇指往上指，那麼，其它的手指都從 y-軸指向 x-軸。

不論坐標軸是何種取向，將坐標系統做任何角度的旋轉，取向仍舊會保持不變。

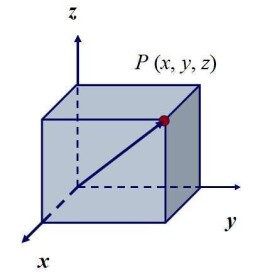
直角坐標系的 x-軸，y-軸，與 z-軸必須相互垂直。稱包含 z-軸的直線為 z-線。在三維空間里，當我們設定了 x-軸，y-軸的位置與方向的同時，我們也設定了 z-線的方向。可是，我們仍舊必須選擇，在 z-線以原點為共同點的兩條半線中，那一條半線的點的坐標是正值的，那一條是負值的？這兩種不同的坐標系統，稱為右手坐標系與左手坐標系。右手坐標系又稱為標準坐標系，或正值坐標系。

右手坐標系這名詞是由右手定則而來的。先將右手的手掌與手指伸直。然後，將中指指嚮往手掌的掌面 半空間，與食指呈直角關係。再將大拇指往上指去，與中指，食指都呈直角關係。則大拇指，食指，與中指分別表示了右手坐標系的 x-軸，y-軸，與 z-軸。同樣地，用左手也可以表示出左手坐標系。因為我們用二維畫面來展示三維物體，會造成扭曲或模稜兩可的圖形。指向下方與右方的軸，也有指向讀者的意思；而位置居於中間的軸，也有指向讀者正在看的方向的意思。平行於 xy-平面的紅色圓形曲箭，其紅色箭頭從 z-軸前面經過，表示從 x-軸往y-軸的旋轉方向。

在數學中，極坐標系是一個二維坐標系統。

該坐標系統中任意位置可由一個夾角和一段相對原點—極點的距離來表示。極坐標系的應用領域十分廣泛，包括數學、物理、工程、航海以及機器人領域。在兩點間的關係用夾角和距離很容易表示時，極坐標系便顯得尤為有用；而在平面直角坐標系中，這樣的關係就只能使用三角函數來表示。對於很多類型的曲線，極坐標方程是最簡單的表達形式，甚至對於某些曲線來說，只有極坐標方程能夠表示。

在1671年寫成，1736年出版的《流數術和無窮級數》一書中，艾薩克·牛頓第一個將極坐標系應用於表示平面上的任何一點。牛頓在書中驗證了極坐標和其他九種坐標系的轉換關係。

在1691年出版的《博學通報》一書中雅各布·伯努利正式使用定點和從定點引出的一條射線，定點稱為極點，射線稱為極軸。平面內任何一點的坐標都通過該點與定點的距離和與極軸的夾角來表示。伯努利通過極坐標系對曲線的曲率半徑進行了研究。

圓柱坐標系（cylindrical coordinate system）是一種三維坐標系統。它是二維極坐標系往 z-軸的延伸。添加的第三個坐標專門用來表示 P 點離 xy-平面的高低。按照國際標準化組織建立的約定 (ISO 31-11) ，徑向距離、方位角、高度，分別標記為。三維空間里，有許多各種各樣的坐標系。圓柱坐標系只是其中一種。圓柱坐標系與其他坐標系的變換需要用到特別的方程式。

在數學里，球坐標系（英語：Spherical coordinate system）是一種利用球坐標表示一個點 p 在三維空間的位置的三維正交坐標系。

球坐標的幾何意義：原點與點 P 之間的徑向距離r，原點到點 P 的連線與正 z-軸之間的天頂角θ，以及原點到點 P 的連線，在 xy-平面的投影線，與正 x-軸之間的方位角φ。

拋物線坐標系是一種二維正交坐標系，兩個坐標的等值曲線都是共焦的拋物線。將二維的拋物線坐標系繞著拋物線的對稱軸旋轉，則可以得到三維的拋物線坐標系。實際上，拋物線坐標可以應用在許多物理問題。例如，斯塔克效應 (Stark effect) ，物體邊緣的位勢論，以及拉普拉斯-龍格-冷次向量的保守性。

是一種三維正交坐標系。往 z-軸方向延伸二維的拋物線坐標系，則可得到拋物柱面坐標系。其坐標曲面是共焦的拋物柱面。拋物柱面坐標可以應用於許多物理問題。例如，物體邊緣的位勢論。拋物柱面坐標有一個經典的應用，這是在解析像拉普拉斯方程或亥姆霍茲方程這類的偏微分方程式。在這些方程式里，拋物柱面坐標允許分離變數法的使用。

二維雙極坐標系是一個正交坐標系。學術界上有三種常用的雙極坐標系。除了在這裡討論的坐標系以外，另外兩種是雙心坐標系與雙角坐標系。

這裡所要討論的雙極坐標系建立於阿波羅尼奧斯圓。σ的等值曲線是圓圈。τ的等值曲線也是圓圈。兩組圓圈互相垂直相交。雙極坐標系有兩個焦點，其直角坐標通常分別設定為與。所以，這兩個焦點都處於直角坐標系的 x-軸。

雙極坐標系是好幾種三維正交坐標系的原始模。往 z-軸方向延伸，則可得到雙極圓柱坐標系。繞著 x-軸旋轉，即可得到雙球坐標系。繞著 y-軸旋轉，就可得到圓環坐標系。

在數學里，雙曲坐標系是一種二維坐標系統。它可以用來表達一個點在二維平面的第一象限的位置。

橢圓坐標系是幾種三維正交坐標系的基礎。將橢圓坐標系往 z-軸方向投射，則可以得到橢圓柱坐標系。將橢圓坐標系繞著 x-軸旋轉，就可以得到長球面坐標系，而繞著 y-軸旋轉，又可以得到扁球面坐標系；在這裡，x-軸是連接兩個焦點的直軸，y-軸是在兩個焦點中間的直軸。

橢圓坐標最經典的用法是在解析像拉普拉斯方程或亥姆霍茲方程這類的偏微分方程式。在這些方程式里，橢圓坐標允許分離變數法的使用。

是一種三維正交坐標系。設定二維橢圓坐標系包含於 xz-平面；兩個焦點的直角坐標分別為與 。將橢圓坐標系繞著 z-軸旋轉，則可以得到扁球面坐標系。（假若，繞著 y-軸旋轉，則可以得到長球面坐標系。）橢圓坐標系的兩個焦點，變為一個半徑為的圓圈，包含於三維空間的 xy-平面。稱這圓圈為焦圓，又稱為參考圓。扁球面坐標系可以被視為橢球坐標系的極限案例，其兩個最大的半軸的長度相同。

當邊界條件涉及扁球面或旋轉雙曲面時，扁球面坐標時常可以用來解析偏微分方程式。例如，關於佩蘭摩擦因子(Perrin friction factors) 的計算，扁球面坐標扮演了極重要的角色。讓·佩蘭因此而榮獲 1926 年諾貝爾物理獎。佩蘭摩擦因子決定了分子的旋轉擴散 (rotational diffusion)。這程序又影響了許多科技，像蛋白質核磁共振光譜學 (protein NMR) ，的可行性。

應用這程序，我們可以推論分子的流體動力體積與形狀。扁球面坐標也時常用來解析電磁學（例如，扁球形帶電的分子的電容率），聲學（例如，聲音通過圓孔時產生的散射），流體動力學（水通過消防水帶的噴口），擴散理論（紅熱的錢幣在水裡的冷卻），等等方面的問題。

是一種三維正交坐標系。設定二維橢圓坐標系包含於 xz-平面；兩個焦點的直角坐標分別為與 。將橢圓坐標系繞著 z-軸旋轉，則可以得到長球面坐標系。（假若，繞著 y-軸旋轉，則可以得到扁球面坐標系。）橢圓坐標系的兩個焦點，包含於 z-軸。長球面坐標系可以被視為橢球坐標系的極限案例，其兩個最短的半軸的長度相同。

是一種三維正交坐標系。往 z-軸方向延伸二維的橢圓坐標系，則可得到橢圓柱坐標系；其坐標曲面是共焦的橢圓柱面與雙曲柱面。橢圓柱坐標系的兩個焦點的直角坐標分別為與，都處於直角坐標系的 x-軸。

橢圓柱坐標最經典的用途是在解析像拉普拉斯方程或亥姆霍茲方程這類的偏微分方程式。在這些方程式里，橢圓柱坐標允許分離變數法的使用。三維的波方程，假若用橢圓柱坐標來表達，則可以用分離變數法解析，形成了馬蒂厄微分方程 (Mathieu differential equation)。

是一種三維正交坐標系。設定二維橢圓坐標系包含於 xz-平面；兩個焦點的直角坐標分別為與。將雙極坐標系繞著 z-軸旋轉，則可以得到圓環坐標系。雙極坐標系的兩個焦點，變為一個半徑為 a 的圓圈，包含於圓環坐標系的 xy-平面。稱這圓圈為焦圓，又稱為參考圓。

是一種三維正交坐標系。設定二維雙極坐標系包含於 xz-平面。設定這雙極坐標系的兩個焦點 F1與 F2包含於 z-軸。將雙極坐標系繞著 z-軸旋轉，則可以得到雙球坐標系。在這二維雙極坐標系裡，坐標σ的等值曲線是圓圈。經過旋轉后，圓圈變成一個環面，而圓圈的圓心變成一個包含於 xy-平面的圓圈，稱為環心圓。稱環心圓至環面的距離為環小半徑。

是一種三維正交坐標系。它的三個坐標曲面分別為同心圓球面，錐軸為 x-軸的圓錐面，錐軸為 z-軸的圓錐面。