非線性系統理論
非線性系統理論
非線性系統理論,nonlinear systems theory,是在自動控制理論中研究非線性系統的運動規律和分析方法的一個分支學科。
一般來說,這樣的模型是由非線性微分方程和非線性差分方程給出的,對這類模型的辨別可以採用線性化,展開成特殊函數等方法。非線性系統理論的研究對象是非線性現象,它反映出非線性系統運動本質的一類現象,不能採用線性系統的理論來解釋,主要原因是非線性現象有頻率對振幅的依賴性、多值響應和跳躍諧振、分諧波振蕩、自激振蕩、頻率捕捉、非同步抑制、分岔和混沌等。
非線性系統的一個最重要的特性是不能採用疊加原理來進行分析,這就決定了在研究上的複雜性。非線性系統理論遠不如線性系統理論成熟和完整。由於數學處理上的困難,所以至今還沒有一種通用的方法可用來處理所有類型的非線性系統。
非線性系統理論的研究對象是非線性現象,它是反映非線性系統運動本質的一類現象,不能採用線性系統的理論來解釋。主要的非線性現象有頻率對振幅的依賴性、多值響應和跳躍諧振、分諧波振蕩、自激振蕩、頻率捕捉、非同步抑制、分岔和混沌等。
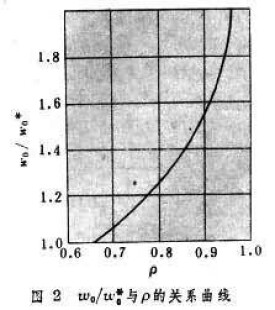
頻率對振幅的依賴性
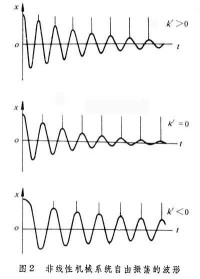
非線性系統理論
多值響應和跳躍諧振
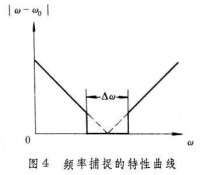
非線性系統理論
分諧波振蕩
這種非線性現象只出現在某些非線性系統的穩態振蕩中。分諧波振蕩被激發后,在一定的頻率範圍內,不管外作用函數的頻率 ω如何改變,穩態振蕩的頻率始終為 ,其中 n為某個正整數稱為分諧波振蕩的階數。分諧波振蕩的產生取決於系統的參數,並且必須在某種衝擊,如突然改變外作用函數的振幅或頻率。
自激振蕩
又稱極限環,是非線性系統中一類很重要的和得到廣泛研究的非線性現象(見相平面法)。
頻率捕捉
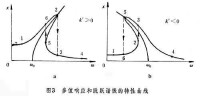
非線性系統理論
非同步抑制
又稱信號穩定。其機制是,採用使系統處於頻率為 的強迫振蕩狀態,來抑制和避免系統中可能出現的頻率為 的極限環振蕩。這裡兩個頻率 和 是互不相關的。
在很多實際系統中都能見到的,運動穩態點會隨著系統參數變動到臨界值而不斷發生分岔的一種非線性現象(見分岔理論)。
混沌
1963年氣象學家E.N.洛倫茨在研究天氣預報問題的大氣對流模型的數值實驗中首先發現的一種非線性現象。其特點是某些非線性系統在一定參數範圍內變得對初始條件非常敏感,會導致非周期的、看起來很混亂的輸出。後來,在生態系統等研究中也發現混沌現象。80年代以來,關於混沌的研究已成為一個非常活躍的領域,得到了一些嚴格的數學結果,但更多的是計算機實驗,真正的物理實驗也在日益增多。
對於非線性系統尚未建立起象線性系統的分析那樣成熟和系統的一套方法,在應用上比較有效的主要方法有四種。
等效線性化方法 主要用於分析非線性程度較低的非線性系統。其實質是把非線性問題近似地加以線性化,然後去解決已線性化的問題。描述函數法、分段線性化法、小參數法等都屬於這種方法。
直接分析方法 建立在直接處理系統的實際的或簡化后的非線性微分方程基礎上的分析方法,不管非線性程度的高低都可適用。相平面法、李雅普諾夫第二方法(見李雅普諾夫穩定性理論)等都屬於這種方法。
雙線性系統理論 對於雙線性系統這一特殊類型非線性系統建立的分析和綜合方法。
60年代以來,非線性系統理論的發展進入了一個新階段。對分岔現象和混沌現象的研究已成為非線性系統理論中很受重視的一個方向。突變理論、耗散結構理論和協同學這些也以非線性系統為研究對象的新興學科相繼出現,它們的方法和結果將對非線性系統理論乃至整個系統科學產生重要影響。此外,隨著微分幾何方法(特別是微分流形理論)引入於非線性系統的研究並得到了某些有意義的結果,非線性泛函分析、奇異攝動方法和大範圍分析等現代數學分支也已開始用於非線性系統理論的研究。

非線性系統理論
作 者:方勇純
出版社:清華大學出版社
出版時間: 2009年05月
ISBN: 9787302193036
開本: 16開
定價: 22元
《非線性系統理論》適用對象為高等院校自動化專業研究生,以及從事非線性控制系統分析與設計的工程技術人員。非線性控制是近年來控制理論界非常活躍的一個研究領域。本教材重點討論基於李雅普諾夫方法的非線性控制及其在實際系統中的具體應用,首先介紹李雅普諾夫穩定性理論,然後依次對非線性系統精確線性化、自適應控制、魯棒控制、學習控制等方法進行討論,同時應用李雅普諾夫理論對於這些控制方法進行穩定性分析。
在內容安排上,第2、3章是理論基礎。其中,第2章重點介紹書中所涉及的數學背景,主要包括用於信號分析的幾個重要定理以及少量的微分幾何基礎知識。第3章討論李雅普諾夫基本理論,給出各種穩定性的數學定義,並重點介紹李雅普諾夫穩定性理論和拉賽爾不變性原理。第4~8章是對於自適應控制等多種方法的具體介紹和理論分析,各章相互獨立,讀者可以選擇感興趣的方法進行學習。第8~10章主要介紹非線性控制方法在典型對象,如機器人系統、欠驅動吊車系統和磁懸浮系統中的具體應用。
方勇純,男,南開大學教授,博士生導師,IEEE高級會員,中國自動化學會控制理論專業委員會、智能自動化專業委員會委員。1996年和1999年分別獲得浙江大學工學學士和碩士學位。2002年12月畢業於美國克萊姆森大學(Clemson University)電機系,獲工學博士學位。2002年12月至2003年11月在美國康奈爾大學(Cornell University)機械與航天工程系進行博士后研究。主要研究方向為機器人視覺伺服,非線性控制及應用,基於原子力顯微鏡的微納米系統。2006年入選教育部“新世紀優秀人才支持計劃”,2008年獲天津青年科技獎提名獎,2009年獲“天津市優秀留學人員”榮譽稱號。
第1章 非線性系統簡介
1.1 引言
1.2 非線性系統的複雜性能
1.2.1 非線性系統的多平衡點特性
1.2.2 極限環
1.2.3 混沌
1.2.4 其他非線性現象
1.3 非線性控制的重要意義
1.4 常見的非線性系統設計與分析方法
1.4.1 相平面分析法
1.4.2 描述函數法
1.4.3 李雅普諾夫法
1.5 本書的主要內容安排
習題
參考文獻
第2章 數學預備知識
2.1 范數及其性質
2.2 函數的連續性
2.3 函數的正定性分析
2.4 信號分析基本定理
2.5 微分幾何基本知識
2.5.1 微分流形及切空間
2.5.2 李導數與李括弧運算
2.5.3 伏柔貝尼斯定理
習題
參考文獻
……
機械工業出版社圖書
| 書號: | 28801 | ISBN: | 978-7-111-28801-5 |
| 作者: | 康惠駿 編著 | 印次: | 1-1 |
| 責編: | 於蘇華 | 開本: | 16 |
| 字數: | 381千字 | 定價: | 32.0 |
| 所屬叢書: | 普通高等教育電氣工程與自動化類"十一五"規劃教材 | ||
| 裝訂: | 平 | 出版日期: | 2010-03-26 |

非線性系統理論
本書主要介紹非線性系統的基本理論和一些最新進展。內容包括:近代數學基礎、非線性系統基本理論、系統的可控性和可觀測性、局部分解、反饋線性化、解耦控制、系統的鎮定、Euler-Lagrange系統控制和哈密頓系統控制等。本書注重概念及主要理論的講述,理論聯繫實際,重點突出,反映了該領域的基本理論和最新研究成果與進展。本書可作為控制科學與工程等學科的碩士與博士研究生教材,也可作為其他相關科研領域的廣大科技工作者的參考書。
目錄前言
第1章數學基礎1
1 1集合1
1 2映射2
1 3拓撲空間4
1 4歐氏空間5
1 5微分流形8
1 6切向量和切空間11
1 7向量場的積分曲線14
1 8微分同胚的導出映射16
1 9李導數17
1 10向量場的李代數19
1 11分佈與余分佈22
1 12幾個基本定理24
1 13代數基礎28
1 13 1運算28
1 13 2代數系統29
1 14小結與評述33
第2章非線性系統基本理論37
2 1微分方程的基本概念37
2 2常微分方程的基本理論38
2 2 1自治系統常點附近的向量場39
2 2 2常點附近向量場的直化定理39
2 2 3解的存在性定理40
2 2 4解的局部唯一性定理40
2 2 5解對參數的連續依賴和
可微性定理41
2 2 6解的延拓定理41
2 2 7非自治系統的基本理論41
2 3動力系統基礎43
2 3 1動力系統43
2 3 2軌線、龐加萊映射45
2 3 3拓撲軌線等價和拓撲軌線共軛46
2 3 4線性化、雙曲性和穩定性46
2 3 5穩定流形和不穩定流形48
2 3 6中心流形49
2 3 7結構穩定性和通有性50
2 3 8分支52
2 3 9普用分支和普適開折55
2 4小結與評述60
第3章可控性、可觀測性
和局部分解62
3 1可控性62
3 2可觀測性73
3 3局部分解79
3 4小結與評述85
第4章非線性系統的線性化87
4 1坐標變換線性化87
4 2狀態反饋線性化93
4 3部分狀態反饋線性化97
4 4完全線性化101
4 5全局線性化108
4 6多變數系統的推廣111
4 7實例分析115
4 8幾個重要的數學定理119
4 9小結與評述120
第5章非線性系統的解耦控制122
5 1狀態方程無反饋解耦122
5 2狀態方程反饋解耦126
5 3靜態反饋輸入輸出解耦128
5 4動態反饋輸入輸出解耦133
5 5小結與評述141
第6章非線性系統的鎮定142
6 1通過線性化的局部穩定性和鎮定142
6 2使用Lyapunov直接方法
的局部鎮定144
6 3中心流形理論與局部鎮定147
6 4非線性系統的分段光滑鎮定151
6 5小結與評述155
第7章Euler Lagrange系統控制156
7 1Euler Lagrange系統的基本概念156
7 1 1Euler Lagrange方程156
7 1 2耗散性、無源性和內部
穩定性159
7 1 3EL系統的互聯160
7 1 4EL系統的穩定性161
7 2定點調節162
7 2 1狀態反饋控制162
7 2 2欠驅動系統的輸出反饋鎮定165
7 2 3實例分析167
7 3小結與評述169
第8章Hamilton系統控制170
8 1埠受控與埠受控耗散
Hamilton系統170
8 1 1Hamilton方程170
8 1 2埠受控Hamilton
系統170
8 1 3埠受控耗散Hamilton系統171
8 1 4實例分析——串聯RLC電路的
PCHD系統模型171
8 2PCHD系統的能量平衡
與能量成型172
8 2 1PCHD系統的能量平衡172
8 2 2PCHD系統的能量成型原理173
8 2 3通過能量平衡進行控制173
8 3互聯控制174
8 3 1子系統互聯與系統無源性174
8 3 2通過互聯控制進行能量成型175
8 4互聯和阻尼配置的無源性
控制178
8 4 1控制作為一個狀態調製源178
8 4 2互聯和阻尼配置的方法181
8 5小結與評述184
第9章Maple在非線性系統理論
中的應用186
9 1計算機代數系統Maple186
9 1 1Maple的結構與界面186
9 1 2Maple的基本功能188
9 2Maple在幾何基礎中的應用197
9 2 1李導數和李括弧197
9 2 2分佈和余分佈199
9 2 3用Maple計算李導數
和李括弧200
9 2 4實例分析203
9 3Maple在可控性和可觀測性分析
中的應用206
9 3 1用Maple分析系統可接近性206
9 3 2用Maple分析系統可觀測性209
9 3 3實例分析211
9 4Maple在精確線性化設計中的應用215
9 4 1線性化的定義及定理215
9 4 2Maple在坐標變換線性化
中的應用216
9 4 3Maple在坐標變換完全線性
化中的應用218
9 4 4Maple在狀態方程反饋精確
線性化中的應用221
9 4 5實例分析223
9 5Maple在輸入輸出解耦控制
中的應用224
9 5 1輸入輸出解耦控制224
9 5 2用Maple討論輸入輸出解耦
控制問題225
9 5 3實例分析229
9 6小結與評述232
參考文獻234