非線性電路
非線性電路
含有非線性元件的電路。這裡的非線性元件不包括獨立電源。非線性元器件在電工中得到廣泛應用。非線性電路的研究和其他學科的非線性問題的研究相互促進。非線性電路中,參數(電阻、電感、振幅、頻率等)改變到分岔值時響應會突變,出現跳躍現象。非線性電路可以出現的一種穩態響應波形,看似無規律可循,類似隨機輸出。
非線性電路
線性電路通常只有一個穩態。但有些非線性電路的穩態可以不止一個。例如,用刀開關斷開某個直流電路,當開關的刀和固定觸頭之間的距離不夠大(例如距離為d)時,刀與觸頭之間可以出現穩定的電弧,電路中有電流,這是電路的一個穩態;增加上述距離使電弧熄滅后,再使此距離減少到d,卻見不到電弧,電路中沒有電流,這是另一個穩態。電弧的非線性特性使這個電路有兩個穩態。電路處於何種穩態由起始條件決定。
在有些非線性電路里,獨立電源雖然是直流電源,電路的穩態電壓(或電流)卻可以有周期變化的分量,電路里出現了自激振蕩。音頻信號發生器的自激振蕩電路中因有放大器這一非線性元件,可產生其波形接近正弦的周期振蕩。
在含有直流獨立電源的線性電路中,穩態下的電壓、電流是不隨時間變化的直流電壓、直流電流。但在有些非線性電路里,獨立電源雖然是直流電源,電路的穩態電壓(或電流)卻可以有周期變化的分量,電路里出現了自激振蕩。例如,音頻信號發生器的自激振蕩電路中因有放大器這一非線性元件而成為非線性電路。這個電路可以產生其波形接近正弦的周期振蕩。自激振蕩可以分為兩種。軟激勵:電路接通后就能激起振蕩。硬激勵:電路接通后,一般不能激起振蕩,電路處於直流穩態。必須另外加一個幅度較大、作用時間很短的激勵,電路里才會激起振蕩。在這樣的電路中便有兩個穩態:一個是直流穩態,一個是含周期振蕩的穩態。
正弦激勵作用於非線性電路且電路有周期響應時,響應的波形一般為非正弦的,含有高次諧波分量或次諧波分量。例如,整流電路中的電流常會有高次諧波分量。也可以有頻率低於激勵頻率的次諧波分量。整流電路中的電流常會有高次諧波分量。將鐵心線圈和合適的電容器串聯接到正弦電壓源上,構成鐵磁諧振電路,其中的電流可含有頻率是電源頻率的次諧波分量,稱次諧波。
非線性電路中,參數(電阻、電感、振幅、頻率等)改變到分岔值時響應會突變,出現跳躍現象。鐵磁諧振電路中就會發生電流跳躍現象。電路的響應與電路的各種參數有關。電阻、電感、正弦電源的振幅和頻率都是參數。當某個參數有微小變化時,響應一般也有微小變化。但在非線性電路里,當參數改變到分岔值時,響應會突變,出現跳躍現象。考慮一個有合適電容值的鐵磁諧振電路,以正弦電壓源的有效值U 作為控制參數。平滑地、緩慢地改變U 時,電流有效值I一般隨之平滑地變化,圖中兩條實線表示這種變化,箭頭代表變化方向。當電壓U由0增加時,電流按曲線①變化。當U 達到分岔值U2時,電流會突然增加,以後電流沿曲線②變化。當U由大於U2的值減少到分岔值U1時,電流會突然減少。電流跳躍性變化用圖中虛線表示。平滑地改變電源的頻率,也可以看到類似的現象。
正弦激勵作用於自激振蕩電路時,若激勵頻率與自激振蕩頻率二者相差很小,響應會與激勵同步。正弦激勵作用於自激振蕩電路時,看來有兩種頻率的振蕩在電路里起作用,一個是激勵的頻率,一個是自激振蕩頻率。但當二者相差很小時,電路里只存在頻率為激勵頻率的振蕩:響應與激勵同步。這種現象稱為頻率捕捉。
20世紀20年代,荷蘭人B.范德坡爾描述電子管振蕩電路的方程,成為研究混沌現象的先聲。
非線性電路可以出現的一種穩態響應波形,看似無規律可循,類似隨機輸出。它的頻譜中有連續頻譜成分。響應對起始條件極為敏感。在兩組相差極微小的起始條件下,經過較長的時間以後兩個響應的波形差別很大。這種穩態響應是一種混沌現象。在三階(或三階以上)自治電路和二階(或二階以上)非自治電路里可以出現混沌。低階電路的混沌常作為理論研究對象。
非線性是在自然界廣泛存在的自然規律,相對於我們熟悉的線性要複雜得 多。隨著物理學研究的不斷深入,非線性問題逐漸被重視起來,現已出現了多個 分支,混沌便是其中之一。混沌現象在生活中廣泛存在,如著名的蝴蝶效應、湍 流、昆蟲繁衍等。要直觀地演示混沌現象,採用非線性電路是一個非常好的選擇。能產生混沌 現象的自治電路至少滿足以下三個條件:
1)有一個非線性元件,
2)有一個用 於耗散能量的電阻,
3)有三個存儲能量的元件。如圖 1 所示的蔡氏電路(Chua's circuit)
[3,4]是一個符合上述條件、非常簡潔的非線性電路,由華裔物理學家蔡紹 棠(Leon O. Chua)教授於 1983 年提出並實現。近年來,非線性電路的研究領 域有了長足進展,新的混沌與超混沌電路的理論設計與硬體實現等問題備受人 們關注。如 Chen 氏電路、Colpitts 振蕩電路、基於 SETMOS 的細胞神經網路 結構的蔡氏電路,都能用於研究混沌現象,並有不同的應用領域。
實驗原理
在眾多的非線性電路中,蔡氏電路因其結構簡單、現象明晰,成為教學實驗 中讓學生接觸、了解混沌現象的最佳選擇,大量基於蔡氏電路的實驗儀器[9-11]被 廣泛應用於高校實驗教學。蔡氏電路(如圖一所示)的主要元件有可調電阻 R (電 路方程中以電導 做參數,以下方程求解過程都用 G 來表示,而涉及實驗 的內容採用 R 表示) 、電容 C1 和 C2、電感 L 以及非線性負阻 Nr。它的運行狀態 可以用以下方程組來描述:
(1)其中 為 (或負阻)兩端的電壓,為(或)兩端的電壓, 為通 過 的電流,錯誤!未指定書籤。為非線性負阻的 特性函數,其表達式 錯誤!未指定書籤。為:
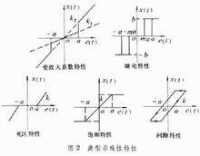
式中各參數和變數的具體意義間圖 3。從的表達式看出,分三段,且每 段都是線性的,所以我們可以將求解分三個區間來進行。由於兩側區間基本對稱,可以一併求解。
圖 1:蔡氏電路示意圖
構成一個三維的狀態空間,稱為相空間,相空間的狀態點記為
。混沌實驗儀中一般演示 點的相軌跡在 平面的二維投
T
影,可用雙蹤示波器的模式來觀察,即常說的李薩如圖形。在每個區間內,方程(1)都可以改寫成如下形式的線性方程:
&
& 其中 為三維矢量,為三階矩陣。方程(3)在 時的解即為相空間
& 的不動點 。原方程組的解即可寫為線性齊次方程 的
通解與不動點特解 的和。方程(3)的本徵值方程為,若 存在三個本 征值 ,齊次方程的解即為: 其中 為 對應的本徵向量,由初始狀態 決定。在有些情況下, 有一個實本徵值 和一對共軛的複本徵值 ,方程的解 可以寫成:
(4)
(5)
式中 是實本徵值對應的本徵向量,是共軛的複本徵值對應的本徵向量。 由初始狀態決定。綜上所述,蔡氏電路方程組的解為:
(6)
我們把實本徵向量 方向標記為 ,把 和 張成的平面記為 。齊次方 程解的獨立分量在 方向,在平面 內。方程的解隨著時間演化具有 如下性質:如果指數衰減到 0;如果沿著 Er 方向指數增長。由此可見,對於任何一條相軌跡 方向上的分量恆正或恆負,所以它始 錯誤! 、錯誤)終都無法穿越 平面(圖錯誤!未定義書籤。錯誤!未定義書籤。。如果 錯誤 未定義書籤。錯誤!未定義書籤。且 ,則 在 平面內螺旋離開不動點;若在 平面內螺 旋收縮到不動點 。這些性質在進行每個區域分析時都非常有用。非線性負阻的結構如圖 2 所示,由兩個封裝在一起的運算放大器(雙運算 放大器集成電路 )和 6 個定值電阻 、 ,精度 1%)構成,輸入電源電壓。理想的非線性負阻具有如
出
,
。
圖 2:非線性負阻的內部結構
圖 3:理想非線性負阻 I-V 特性(示意圖)
實驗內容
一、各種混沌現象的觀測 各種混沌現象的觀測 用圖 1 所示的方法,調節可調電阻 R,觀察單周期、雙周期、陣發混沌、三 周期、單吸引子、雙吸引子等相圖,並記錄各種相圖對應的 U1,U2 的信號特點。二、測量非線性負阻的 I-V特性 V 1、用如圖 4 所示的方法,用示波器驅動,分別在和 等頻率測量非線性負阻的 I-V 特性,討論不同頻率時 I-V 曲線的特點。
圖 4:外部信號掃描測量 I-V 特性電路圖
2、用圖 5 所示的方法:在電路中接入一個 的採樣電阻,非線性負阻 兩端的電壓 U1 仍在 CH1 端測量,用 端輸出的 r 兩端的電壓代替電流信號 來記錄 I-V 曲線,實驗時利用蔡氏電路自身的振蕩信號代替信號發生器的輸入。 的信號輸入另一雙蹤示波器觀察非線性電路的二位相圖,記錄電路
出現各種混沌狀態時的 I-V 曲線。
3、比較上述兩種方法得到的 I-V 曲線的異同,並討論原因。
4、分析第二種方法得到的結果,並解釋相圖和 I-V 曲線之間的關聯。
圖 5:內置信號掃描測量 I-V 特性電路圖
5、 (選做)用伏安法測量非線性負阻的 I-V 曲線,分析得到的結果。
三、元件參數測量和非線性方程的求解
1、用萬用表測量電路中的電容、電感的值。 (有興趣的同學可查閱萬用表測 電容、電感的原理。 )
2、用函數信號發生器作電源,用伏安法測量電容、電感的值,討論電流、頻率不同時,測量結果的變化。注意:實際有鐵芯電感的等效模型為一個理想電 感和一個損耗電阻的組合。
3、 (選做)用高精度的 LCR 表測量各個元件的參數。
4、用實際測得的實驗參數求解非線性方程組(1) ,找出不同條件下的不動 點,分析不動點的穩定性和解的特點。 (選做)
四、選做)C 調製(選做 設計實驗方法,實現用電容 C 的調節了得到各種混沌相圖,並討論 G 調製 和 C 調製得到的相圖的不同。
五、數值模擬 1、採用四階 Runge-Kutta 法求解方程組(1) ,畫出各種相圖。
2、用 FFT 法分析各種相圖時時域型號的頻率特性。
3、繪製 U1 隨 R 變化的分岔圖,得出單周期、雙周期等混沌狀態時的 R 值,和實驗觀察的結果進行比較。六、(探索)混沌通訊 探索)閱讀文獻,了解混沌通訊的原理和實現方法,從實驗上實現兩台混沌實驗儀
的信號同步,並進行進一步的探索研究。七、(探索)分形 探索)用計算機編程得到各種分形圖形。
上一世紀初量子力學和相對論的發現,因為提出了突破人們傳統思維的新概 念,將人類的世界觀推進到超越經典的領域,而被公認為是物理學或更確切地說 是科學的兩次革命。牛頓創立的經典力學被發現並不始終是正確的。當深入到微 觀尺度()應該取代為量子力學, ,當物體的速度接近於光速() ,則相對論是正確的。
非線性科學作為科學的一個新分支,如同量子力學和相對論一樣,也將我們 引向全新的思想,給予我們驚人的結果。非線性科學的誕生,進一步宣布了牛頓 的經典決定論的局限性。它指出,即使是通常的宏觀尺度和一般物體的運動速度,經典決定論也不適用於非線性系統的混沌軌道的行為分析。非線性科學涵蓋各種 各樣尺度的系統,涉及以任意速率運動的對象,這一事實絲毫不降低這一新學科 的創新性,恰恰相反,剛好說明它具有廣泛的應用性。從這一點來看,其實非線 性科學的誕生和發展更有資格被稱為科學的一場革命。非線性科學,目前有六個主要研究領域,即:混沌、分形、模式形成、孤立 子、元胞自動機,和複雜系統。而構築多種多樣學科的共同主題乃是所研究系統 的非線性。一個系統,如果其輸出不與其輸入成正比,則它是非線性的。例如一個介電 晶體,當其輸出光強不再與輸入光強成正比,就成為非線性介電晶體。例如彈簧,當其位移變得很大時,胡克定律就失效,彈簧變為非線性振子。又例如單擺,僅 當其角位移很小時,行為才是線性的。實際上,自然科學或社會科學中的幾乎所 有已知系統,當輸入足夠大時,都是非線性的。因此,非線性系統遠比線性系統 多得多,客觀世界本來就是非線性的,線性只是一種近似。任何系統在線性區和 非線性區的行為之間存在顯著的定性上的差別。例如單擺的振蕩周期在線性區不 依賴于振幅,但在非線性區,單擺的振蕩周期是隨振幅而變的。從數學上看,非線性系統的特徵是迭加原理不再成立。迭加原理是指描述系 統的方程的兩個解之和仍為其解。迭加原理可以通過兩種方式失效。其一,方程 本身是非線性的。其二,方程本身雖然是線性的,但邊界是未知的或運動的。對於一個非線性系統,哪怕一個小擾動,象初始條件的一個微小改變,都可 能造成系統在往後時刻行為的巨大差異。迭加原理的失效也將導致 Fourier 變換 方法不適用於非線性系統的分析。因此,系統的非線性帶來系統行為的複雜性。對於非線性系統行為的解析研究是相當困難的。更進一步,在許多情況下,對於我們所要研究的系統,方程是未知的,或甚 至可能根本不存在。從分形圖樣生長的簡單的擴散限制聚集模型,到象股票市場 那樣的複雜經濟系統,我們可以舉出無數寫不出方程的非線性系統的例子。混沌是非線性系統的最典型行為,它起源於非線性系統對於初始條件的敏感 依賴性。混沌現象早在上世紀初就已經被法國學者彭加勒所發現,後來又被許多數學家所仔細研究。而學術界近年來對於混沌的特別關注,則起始於七十年代,這是因為美國人費根保姆發現了一些象平方函數重複迭代的很大一類簡單映射 系統居然具有普適的性質。例如倍周期分叉到混沌的道路,分叉參數的漸近收斂 比值,分叉的幾何特徵具有普適標度性等等。而費根保姆工作則是受到了美國氣 象學家洛倫茲與氣象預報有關的重要然而朦朧的工作的啟示。對於混沌系統的如下兩個發現特別有意義。其一,人們發現一個決定論性系 統的行為當處於混沌狀態時似乎是隨機的。僅僅這一發現就迫使所有的實驗家要 重新考察他們的數據,以確定某些曾經歸於雜訊的隨機行為是否應該重新確定為 是由於決定論性混沌而產生的。其二,人們發現很少自由度的非線性系統,就可 能是混沌的而表現為相當複雜。這一發現給我們以這樣的啟示:許多真實系統中 所觀察到的複雜行為其實有一個簡單的起源,那就是混沌。當然,混沌僅僅是復 雜性的起源之一,還存在並非來源於混沌的更複雜的複雜性。決定論性混沌的真實系統(例如氣候)的行為具有明顯的不可預測性。這一 是由於系統對於初始條件的敏感依賴性;二是由於我們在實際中只能近似地測量 或確定系統的初始條件,因為任何測量儀器都只具有有限的解析度。這兩個根本 困難排除了對於任何混沌的真實系統作出長期預報的可能。但從另一方面看,一個被確認為決定論性混沌的系統,在看起來非常複雜的 行為中,卻蘊藏著秩序,因而進行短期預報是可能的。問題在於:如何確定複雜 現象的背後是否存在決定論性混沌的起源?又,如何對一個混沌系統的行為進行 短期預報?對於氣象或股票市場一類系統,由於不可逾越的複雜性,描寫這類系 統的完全方程組,即使是存在的,也決無辦法知道。或者,即使我們能寫出所有 相關的方程組,也不可能有足夠強大功能的計算機來求解這些方程組。但是從實 用的角度考慮,往往只需要對這類系統作一次成功的短期預報。例如,為了在股 票市場上賺錢,炒股者其實只需要能夠預測明天或下一周股票的漲跌趨勢,而不 必知道市場的整個長時間的漲落規律。又例如,如果地球岩石圈的動力學系統被 證明具有決定論性的成分,則地震的預測並非完全不可能,而與地震的中長期預 報相比較,對某一地區的地震進行短臨預報,對於人們的防震更有意義,所以,複雜系統行為的短期預測已經變成混沌的最令人感興趣的一個應用。混沌的另一個重要應用是混沌的控制。這一應用基於如下事實:有許多不穩 定周期軌道嵌入在奇怪吸引子內,我們可以根據需要通過對系統施加一個小擾動
的方法使其中之一穩定並將混沌系統驅動到這一穩定周期軌道狀態。這一技術已 經被成功地應用於各種機械的、電子的、激光的、化學的系統和心臟組織的控制 上。自然界中的大多數特殊結構是由大量相同組元自組織集結而成的。通過某種 簡單的稱之為組織的構造法就可以出現自集結過程。兩種最簡單的構造法是所謂 規則性構造法和隨機性構造法。採用規則性構造法,所有組元就排列成為周期或 准周期方式而構造成例如晶體與合金等等。採用隨機性構造法而形成的結構(或 非結構)的例子有氣體和動物毛髮的分佈等等。而在這兩種極端的構造法之間,則有自相似構造法,這將產生稱為分形的自相似結構。在一個分形中,系統的局 部與整體相似。分形通常具有分數維數。許多分形還可能是不同分數維的分形的 集合,故稱為多重分形。分形和多重分形的名詞,是上世紀八十年代由曼德勃羅 特首先提出的。現在,分形在自然界和數學系統中的廣泛存在性已被人們普遍認 識。例如:凝聚體和膠體、樹木、岩石、山脈、雲彩、星系、粗糙的表面和界面、聚合物和股票市場,無不存在分形。而耗散動力系統中的混沌就表現為相空間中 具有分形結構的奇怪吸引子。奇怪吸引子本身及其吸引域都可能是分形。混沌與 分形之間的這種聯繫至今尚未被充分理解。分形系統的最典型性質是缺少空間的特徵尺度。這一性質可以有三種等價的 表達方式:拓樸自相似性,空間的冪函數律,和標度不變性。類似的,系統中不 存在時間的特徵尺度將導致時間的冪函數律,例如,雜訊。為了解釋分形和 無特徵尺度行為在非平衡系統中的廣泛存在性,丹麥人巴克和中國學者湯超等在 1987 年提出了自組織臨界性假設,現在人們知道,自組織臨界性假設不僅適用 於沙堆,也適用於許多自然系統和社會系統。人們早就注意到河流、樹枝、葉脈、和閃電所形成的分枝之間有驚人的相似 性。這些分枝的斑圖與在雲彩和海藻類群落中所觀察到的緊緻斑圖顯然不同。大 自然是如何生成這些斑圖的?這些不同斑圖模式的形成是否存在一種簡單的原 理或普適的機制?目前還找不到對於這些問題的最終回答,但最近二十年來在這 方面的研究已經取得可喜的進展。混沌理論的成功也開啟了複雜性科學的研究之門。在七八十年代,當人們認 識了混沌之後,對於從自然系統和社會系統中獲得的各種時間序列,莫不用混沌 動力學來進行分析,檢驗其中的決定論性成分,重構其相空間,甚至建立預測模型。混沌理論的成功,打破了人們的一個心理障礙:沒有一個複雜系統因為太復 雜而不可觸摸。人類已經到了直面複雜系統,攻克複雜性難題的時代。複雜性科學所研究的論題跨越非常大的範圍,它包括人類語言、生命起源、計算機、演化生物學、經濟學、心理學、生態學、免疫學,和自旋玻璃、DNA、蜂群、地震以及各種非平衡系統的自組織等等。目前尚無複雜系統的確切定義,這表明複雜性科學尚處於一個新研究領域的萌芽階段。儘管已經發現象諸如複雜 自適應系統和對稱破缺等一般性概念可以用來相當好地描述一大類複雜系統,但 目前還缺乏可以描寫所有複雜系統的統一理論。然而有兩種簡單的思想能夠解釋 許多複雜系統的行為。其一是自組織臨界性,其二是所謂活躍行走原理。自組織 臨界性理論斷言:許多大的動力學系統存在一種趨勢,它會驅動自身到一種沒有 特徵空間尺度和特徵時間尺度的臨界狀態。而活躍行走原理則描述了複雜系統中 的單元是如何通過與所共享的位形的相互作用而與其環境和在彼此之間溝通。活 躍行走原理已經被成功地應用於諸如介電擊穿模式、玻璃中的離子輸運和螞蟻在 食物搜尋時的合作等等非常不同的問題的研究。
以上所概要的非線性動力學系統的物理或科學包含有序和無序的相互影響,也涉及簡單和複雜的交錯。但從數學和處理方法上看,產生所有那些迷人的結果 的原因乃是系統的非線性。客觀世界本來就是非線性的、複雜的。非線性物理就 是一門以非線性系統的普遍規律及客觀世界的複雜性本身為研究對象的學科,它 在上一世紀八十和九十年代蓬勃發展,也將成為新世紀物理學研究的最前沿。
電路靜電放電(ESD)是從事硬體設計和生產的工程師都必須掌握的知識。很多開發人員往往會遇到這樣的情形:實驗室中開發的產品,測試完全通過,但客戶使用一段時間后,即會出現異常現象,故障率也不是很高。一般情況下,這些問題大多由於浪涌衝擊、ESD衝擊等原因造成。在電子產品的裝配和製造過程中,超過的半導體晶元的損壞歸於ESD。隨著微電子技術的廣泛應用及電磁環境越來越複雜,人們對靜電放電的電磁場效應如電磁干擾(EMI)及電磁兼容性(EMC)問題越來越重視。
電路設計工程師一般通過一定數量的瞬間電壓抑制器(TVS)器件增加保護。如固狀器件(二極體)、金屬氧化物變阻器(MOV)、可控硅整流器、其他可變電壓的材料(新聚合物器件)、氣體電子管和簡單的火花隙。隨著新一代高速電路的出現,器件的工作頻率已經從幾kHz上升到GHz,對用於ESD保護的高容量無源器件的要求也越來越高。例如,TVS必須迅速響應到來的浪涌電壓,當浪涌電壓在達到(或更高)峰值時,TVS器件的觸發或調整電壓(與輸入線平行)必須足夠低以便作為一個有效的電壓分配器。安森美半導體的NUC2401是一款帶集成低電容ESD保護功能的共模濾波器,能提供高速USB 2.0信號必要的帶寬、恰當的共模衰減及敏感的內部電路ESD保護,保持了信號的完整性。Vishay公司VBUS054B-HS3是一種單晶元ESD解決方案,線路電容間的差別非常小,可保護雙高速USB埠,以防瞬態電壓信號。還可對略低於接地電平的負瞬態進行鉗位,同時在略高於5V工作電壓範圍對正瞬態進行鉗位。