共找到3條詞條名為三角函數的結果 展開
- GNZ48第三套原創公演
- 數學中屬於初等函數中的超越函數的函數
- GNZ48演唱歌曲
三角函數
數學中屬於初等函數中的超越函數的函數
三角函數是基本初等函數之一,是以角度(數學上最常用弧度制,下同)為自變數,角度對應任意角終邊與單位圓交點坐標或其比值為因變數的函數。也可以等價地用與單位圓有關的各種線段的長度來定義。三角函數在研究三角形和圓等幾何形狀的性質時有重要作用,也是研究周期性現象的基礎數學工具。在數學分析中,三角函數也被定義為無窮級數或特定微分方程的解,允許它們的取值擴展到任意實數值,甚至是複數值。
常見的三角函數包括正弦函數、餘弦函數和正切函數。在航海學、測繪學、工程學等其他學科中,還會用到如餘切函數、正割函數、餘割函數、正矢函數、余矢函數、半正矢函數、半余矢函數等其他的三角函數。不同的三角函數之間的關係可以通過幾何直觀或者計算得出,稱為三角恆等式。
三角函數一般用於計算三角形中未知長度的邊和未知的角度,在導航、工程學以及物理學方面都有廣泛的用途。另外,以三角函數為模版,可以定義一類相似的函數,叫做雙曲函數。常見的雙曲函數也被稱為雙曲正弦函數、雙曲餘弦函數等等。三角函數(也叫做圓函數)是角的函數;它們在研究三角形和建模周期現象和許多其他應用中是很重要的。三角函數通常定義為包含這個角的直角三角形的兩個邊的比率,也可以等價的定義為單位圓上的各種線段的長度。更現代的定義把它們表達為無窮級數或特定微分方程的解,允許它們擴展到任意正數和負數值,甚至是複數值。
起源
公元五世紀到十二世紀,印度數學家對三角學作出了較大的貢獻。儘管當時三角學仍然還是天文學的一個計算工具,是一個附屬品,但是三角學的內容卻由於印度數學家的努力而大大的豐富了。
三角學中”正弦”和”餘弦”的概念就是由印度數學家首先引進的,他們還造出了比托勒密更精確的正弦表。
我們已知道,托勒密和希帕克造出的弦表是圓的全弦表,它是把圓弧同弧所夾的弦對應起來的。印度數學家不同,他們把半弦(AC)與全弦所對弧的一半(AD)相對應,即將AC與∠AOC對應,這樣,他們造出的就不再是”全弦表”,而是”正弦表”了。
印度人稱連結弧(AB)的兩端的弦(AB)為”吉瓦(jiba)”,是弓弦的意思;稱AB的一半(AC) 為”阿爾哈吉瓦”。後來”吉瓦”這個詞譯成阿拉伯文時被誤解為”彎曲”、”凹處”,阿拉伯語是 ”dschaib”。十二世紀,阿拉伯文被轉譯成拉丁文,這個字被意譯成了”sinus”。
古希臘歷史
早期對於三角函數的研究可以追溯到古代。古希臘三角術的奠基人是公元前2世紀的喜帕恰斯。他按照古巴比倫人的做法,將圓周分為360等份(即圓周的弧度為360度,與現代的弧度制不同)。對於給定的弧度,他給出了對應的弦的長度數值,這個記法和現代的正弦函數是等價的。喜帕恰斯實際上給出了最早的三角函數數值表。然而古希臘的三角學基本是球面三角學。這與古希臘人研究的主體是天文學有關。梅涅勞斯在他的著作《球面學》中使用了正弦來描述球面的梅涅勞斯定理。古希臘三角學與其天文學的應用在埃及的托勒密時代達到了高峰,托勒密在《數學彙編》(Syntaxis Mathematica)中計算了36度角和72度角的正弦值,還給出了計算和角公式和半形公式的方法。托勒密還給出了所有0到180度的所有整數和半整數弧度對應的正弦值。
古希臘文化傳播到古印度后,古印度人對三角術進行了進一步的研究。公元5世紀末的數學家阿耶波多提出用弧對應的弦長的一半來對應半弧的正弦,這個做法被後來的古印度數學家使用,和現代的正弦定義一致了。阿耶波多的計算中也使用了餘弦和正割。他在計算弦長時使用了不同的單位,重新計算了0到90度中間隔三又四分之三度(3.75°)的三角函數值表。然而古印度的數學與當時的中國一樣,停留在計算方面,缺乏系統的定義和演繹的證明。阿拉伯人也採用了古印度人的正弦定義,但他們的三角學是直接繼承於古希臘。阿拉伯天文學家引入了正切和餘切、正割和餘割的概念,並計算了間隔10分(10′)的正弦和正切數值表。到了公元14世紀,阿拉伯人將三角計算重新以算術方式代數化(古希臘人採用的是建立在幾何上的推導方式)的努力為後來三角學從天文學中獨立出來,成為了有更廣泛應用的學科奠定了基礎。
阿拉伯歷史
進入15世紀后,阿拉伯數學文化開始傳入歐洲。隨著歐洲商業的興盛,航行、曆法測定和地理測繪中出現了對三角學的需求。在翻譯阿拉伯數學著作的同時,歐洲數學家開始製作更詳細精確的三角函數值表。哥白尼的學生喬治·約阿希姆·瑞提克斯製作了間隔10秒(10″)的正弦表,有9位精確值。瑞提克斯還改變了正弦的定義,原來稱弧對應的弦長是正弦,瑞提克斯則將角度對應的弦長稱為正弦。16世紀后,數學家開始將古希臘有關球面三角的結果和定理轉化為平面三角定理。弗朗索瓦·韋達給出了托勒密的不少結果對應的平面三角形式。他還嘗試計算了多倍角正弦的表達方式。
18世紀開始,隨著解析幾何等分析學工具的引進,數學家們開始對三角函數進行分析學上的研究。牛頓在1669年的《分析學》一書中給出了正弦和餘弦函數的無窮級數表示。Collins將牛頓的結果告訴了詹姆斯·格列高里,後者進一步給出了正切等三角函數的無窮級數。萊布尼茲在1673年左右也獨立得到了這一結果。歐拉的《無窮小量分析引論》(Introductio in Analysin Infinitorum,1748年)對建立三角函數的分析處理做了最主要的貢獻,他定義三角函數為無窮級數,並表述了歐拉公式,還有使用接近現代的簡寫sin.、cos.、tang.、cot.、sec.和cosec.。
弦表的發明
根據認識,弦表的製作似應該是由一系列不同的角出發,去作一系列直角三角形,然後一一量出AC,A’C’,A’’C’’…之間的距離。然而,第一張弦表製作者希臘文學家希帕克 (Hipparchus,約前180~前125)不是這樣作,他採用的是在同一個固定的圓內,去計算給定度數的圓弧AB所對應的弦AB的長。這就是說,希帕克是靠計算,而不是靠工具量出弦長來製表的,這正是他的卓越之處。希帕克的原著早已失傳,我們所知關於希帕克在三角學上的成就,是從公元二世紀希臘著名天文學家托勒密的遺著《天文集》中得到的。雖然托勒密說他的這些成就出自希帕克,但事實上不少是他自己的創造。
據托勒密書中記載,為了度量圓弧與弦長,他們採用了巴比倫人的60進位法。把圓周360等分,把它的半徑60等分,在圓周和半徑的每一等分中再等分60份,每一小份又等分為60份,這樣就得出了托勒密所謂的第一小份和第二小份。很久以後,羅馬人把它們分別取名為”partes minutae primae”和”partes minutae secundae”;後來,這兩個名字演變為”minute”和”second”,成為角和時間的度量上”分”和”秒”這兩個單位的起源。
建立了半徑與圓周的度量單位以後,希帕克和托勒密先著手計算一些特殊圓弧所對應的弦長。比如 60°弧(1/6圓周長)所對的弦長,正好是內接正六邊形的邊長,它與半徑相等,因此得出60°弧對應的弦值是60個半徑單位(半徑長的1/60為一個單位);用同樣的方法,可以算出120°弧、90°弧以及72°弧所對應的弦值。有了這些弧所對應的弦值,接著就利用所稱的”托勒密定理”,來推算兩條已知所對弦長的弧的”和”與”差”所對的弦長,以及由一條弧所對的弦長來計算這條弧的一半所對的弦長。正是基於這樣一種幾何上的推算。他們終於造出了世界上第一張弦表。
傳入中國
三角學輸入中國,開始於明崇禎4年(公元1631年),這年鄧玉函、湯若望和徐光啟合編《大測》,作為曆書的一部份呈獻給朝廷,這是我國第一部編譯的三角學。在《大測》中,首先將sine譯為”正半弦”,簡稱”正弦”,這就成了“正弦”一詞的由來。
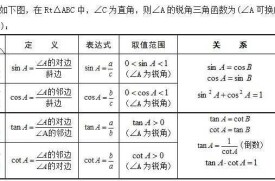
直角三角形三角函數定義
在直角三角形中,當平面上的三點A、B、C的連線,AB、AC、BC,構成一個直角三角形,其中∠ACB為直角。對∠BAC而言,對邊(opposite)a=BC、斜邊(hypotenuse)c=AB、鄰邊(adjacent)b=AC,則存在以下關係:
| 基本函數 | 英文 | 縮寫 | 表達式 | 語言描述 | 三角形 |
| 正弦函數 | sine | sin | a/c | ∠A的對邊比斜邊 | |
| 餘弦函數 | cosine | cos | b/c | ∠A的鄰邊比斜邊 | |
| 正切函數 | tangent | tan | a/b | ∠A的對邊比鄰邊 | |
| 餘切函數 | cotangent | cot | b/a | ∠A的鄰邊比對邊 | |
| 正割函數 | secant | sec | c/b | ∠A的斜邊比鄰邊 | |
| 餘割函數 | cosecant | csc | c/a | ∠A的斜邊比對邊 |
註:正切函數、餘切函數曾被寫作tg、ctg,現已不用這種寫法。
基本三角函數關係的速記方法
六邊形
如右圖,六邊形的六個角分別代表六種三角函數,存在如下關係:
1)對角相乘乘積為1,即sinθ·cscθ=1; cosθ·secθ=1; tanθ·cotθ=1。
2)六邊形任意相鄰的三個頂點代表的三角函數,處於中間位置的函數值等於與它相鄰兩個函數值的乘積,如:sinθ=cosθ·tanθ;tanθ=sinθ·secθ...
3)陰影部分的三角形,處於上方兩個頂點的平方之和等於下頂點的平方值。
變化規律
正弦值在 隨角度增大(減小)而增大(減小),在 隨角度增大(減小)而減小(增大);
餘弦值在 隨角度增大(減小)而增大(減小),在 隨角度增大(減小)而減小(增大);
正切值在 隨角度增大(減小)而增大(減小);
餘切值在 隨角度增大(減小)而減小(增大)。
註:以上其他情況可類推,參考第五項:幾何性質。
除了上述六個常見的函數,還有一些不常見的三角函數。
任意角三角函數定義
在平面直角坐標系xOy中設∠β的始邊為x軸的正半軸,設點P(x,y)為∠β的終邊上不與原點O重合的任意一點,設r=OP,令∠β=∠α
單位圓定義
三角函數
六個三角函數也可以依據半徑為1中心為原點的單位圓來定義。單位圓定義在實際計算上沒有大的價值;實際上對多數角它都依賴於直角三角形。但是單位圓定義的確允許三角函數對所有正數和負數輻角都有定義,而不只是對於在 0 和 π/2弧度之間的角。它也提供了一個圖像,把所有重要的三角函數都包含了。根據勾股定理,單位圓的方程是:對於圓上的任意點(x,y),x²+y²=1。
圖像中給出了用弧度度量的一些常見的角:逆時針方向的度量是正角,而順時針的度量是負角。設一個過原點的線,同x軸正半部分得到一個角θ,並與單位圓相交。這個交點的x和y坐標分別等於cosθ和sinθ。圖像中的三角形確保了這個公式;半徑等於斜邊且長度為1,所以有 sinθ=y/1 和 cosθ=x/1。單位圓可以被視為是通過改變鄰邊和對邊的長度,但保持斜邊等於 1的一種查看無限個三角形的方式。
對於大於 2π 或小於等於2π 的角度,可直接繼續繞單位圓旋轉。在這種方式下,正弦和餘弦變成了周期為 2π的周期函數:對於任何角度θ和任何整數k。
周期函數的最小正周期叫做這個函數的“基本周期”。正弦、餘弦、正割或餘割的基本周期是全圓,也就是 2π弧度或 360°;正切或餘切的基本周期是半圓,也就是 π 弧度或 180°。上面只有正弦和餘弦是直接使用單位圓定義的。
在正切函數的圖像中,在角kπ 附近變化緩慢,而在接近角 (k+ 1/2)π 的時候變化迅速。正切函數的圖像在 θ = (k+ 1/2)π 有垂直漸近線。這是因為在 θ 從左側接近 (k+ 1/2)π 的時候函數接近正無窮,而從右側接近 (k+ 1/2)π 的時候函數接近負無窮。
三角函數
另一方面,所有基本三角函數都可依據中心為O的單位圓來定義,類似於歷史上使用的幾何定義。特別 是,對於這個圓的弦AB,這裡的 θ 是對向角的一半,sinθ是AC(半弦),這是印度的阿耶波多介入的定義。cosθ是水平距離OC,versinθ=1-cosθ是CD。tanθ是通過A的切線的線段AE的長度,所以這個函數才叫正切。cotθ是另一個切線段AF。 secθ=OE和 cscθ=OF是割線(與圓相交於兩點)的線段,所以可以看作OA沿著 A 的切線分別向水平和垂直軸的投影。DE是 exsecθ= secθ-1(正割在圓外的部分)。通過這些構造,容易看出正割和正切函數在 θ 接近 π/2的時候發散,而餘割和餘切在 θ 接近零的時候發散。
依據單位圓定義,可以做三個有向線段(向量)來表示正弦、餘弦、正切的值。圓O是一個單位圓,P是α的終邊與單位圓上的交點,M點是P在x軸的投影,A(1,0)是圓O與x軸正半軸的交點,過A點做過圓O的切線。
那麼向量MP對應的就是α的正弦值,向量OM對應的就是餘弦值。OP的延長線(或反向延長線)與過A點的切線的交點為T,則向量AT對應的就是正切值。向量的起止點不能顛倒,因為其方向是有意義的。
藉助線三角函數線,我們可以觀察到第二象限角α的正弦值為正,餘弦值為負,正切值為負。
級數定義
只使用幾何和極限的性質,可以證明正弦的導數是餘弦,餘弦的導數是負的正弦。(在微積分中,所有角度都以弧度來度量)。我們可以接著使用泰勒級數的理論來證明下列恆等式對於所有實數x都成立。
這些恆等式經常被用做正弦和餘弦函數的定義。它們經常被用做三角函數的嚴格處理和應用的起點(比如,在傅里葉級數中),因為無窮級數的理論可從實數系的基礎上發展而來,不需要任何幾何方面的考慮。這樣,這些函數的可微性和連續性便可以單獨從級數定義來確立。
“三角學”,英文Trigonometry。現代三角學一詞最初見於希臘文。最先使用Trigonometry這個詞的是皮蒂斯楚斯( Bartholomeo Pitiscus,1516-1613),他在1595年出版一本著作《三角學:解三角學的簡明處理》,創造了這個新詞。它是由τριγωυου(三角形)及μετρει υ(測量)兩字構成的,原意為三角形的測量,或者說解三角形。古希臘文里沒有這個字,原因是當時三角學還沒有形成一門獨立的科學,而是依附於天文學。因此解三角形構成了古代三角學的實用基礎。
早期的解三角形是因天文觀測的需要而引起的。還在很早的時候,由於墾殖和畜牧的需要,人們就開始作長途遷移;後來,貿易的發展和求知的慾望,又推動他們去長途旅行。在當時,這種遷移和旅行是一種冒險的行動。人們穿越無邊無際、荒無人煙的草地和原始森林,或者經水路沿著海岸線作長途航行,無論是那種方式,都首先要明確方向。那時,人們白天拿太陽作路標,夜裡則以星星為指路燈。太陽和星星給長期跋山涉水的商隊指出了正確的道路,也給那些沿著遙遠的異域海岸航行的人指出了正確的道路。
就這樣,最初的以太陽和星星為目標的天文觀測,以及為這種觀測服務的原始的三角測量就應運而生了。因此可以說,三角學是緊密地同天文學相聯繫而邁出自己發展史的第一步的。
三角學問題的提出:三角學理論的基礎,是對三角形各元素之間相依關係的認識。一般認為,這一認識最早是由希臘天文學家獲得的。當時,希臘天文學家為了正確地測量天體的位置。研究天體的運行軌道,力求把天文學發展成為一門以精確的觀測和正確的計算為基礎之具有定量分析的科學。他們給自己提出的第一個任務是解直角三角形,因為進行天文觀測時,人與星球以及大地的位置關係,通常是以直角三角形邊角之間的關係反映出來的。在很早以前,希臘天文學家從天文觀測的經驗中獲得了這樣一個認識:星球距地面的高度是可以通過人觀測星球時所採用的角度來反映的;角度(∠ABC)越大,星球距地面(AC)就越高。然而,星球的高度與人觀測的角度之間在數量上究竟怎麼樣呢?能不能把各種不同的角度所反映的星球的高度都一一算出來呢?這就是天文學向數學提出的第一個課題-製造弦表。所謂弦表,就是在保持AB不變的情況下可以供查閱的表,AC的長度與∠ABC的大小之間的對應關係。
三角函數
獨立三角學的產生:雖然後期的阿拉伯數學家已經開始對三角學進行專門的整理和研究,他們的工作也可以算作是使三角學從天文學中獨立出來的表現,但是嚴格地說,他們並沒有創立起一門獨立的三角學。真正把三角學作為數學的一個獨立學科加以系統敘述的,是德國數學家雷基奧蒙坦納斯。
雷基奧蒙坦納斯是十五世紀最有聲望的德國數學家約翰·謬勒的筆名。他生於哥尼斯堡,年輕時就積極從事歐洲文藝復興時期作品的收集和翻譯工作,並熱心出版古希臘和阿拉伯著作。因此對阿拉伯數學家們在三角方面的工作比較了解。
1464年,他以雷基奧蒙坦納斯的名字發表了《論各種三角形》。在書中,他把以往散見在各種書上的三角學知識,系統地綜合了起來,成了三角學在數學上的一個分支,
現代三角學的確認:直到十八世紀,所有的三角量:正弦、餘弦、正切、餘切、正割和餘割,都始終被認為是已知圓內與同一條弧有關的某些線段,即三角學是以幾何的面貌表現出來的,這也可以說是三角學的古典面貌。三角學的現代特徵,是把三角量看作為函數,即看作為是一種與角相對應的函數值。這方面的工作是由歐拉作出的。1748年,歐拉發表著名的《無窮小分析引論》一書,指出:”三角函數是一種函數線與圓半徑的比值”。具體地說,任意一個角的三角函數,都可以認為是以這個角的頂點為圓心,以某定長為半徑作圓,由角的一邊與圓周的交點P向另一邊作垂線PM后,所得的線段OP、OM、MP(即函數線)相互之間所取的比值,sinα=MP/OP,cosα=OM/OP,tanα= MP/OM等。若令半徑為單位長,那麼所有的六個三角函數又可大為簡化。
歐拉的這個定義使三角學從靜態地只是研究三角形解法的狹隘天地中解脫了出來,使它有可能去反映運動和變化的過程,從而使三角學成為一門具有現代特徵的分析性學科。正如歐拉所說,引進三角函數以後,原來意義下的正弦等三角量,都可以脫離幾何圖形去進行自由的運算。一切三角關係式也將很容易地從三角函數的定義出發直接得出。這樣,就使得從希帕克起許多數學家為之奮鬥而得出的三角關係式,有了堅實的理論依據,而且大大地豐富了。嚴格地說,這時才是三角學的真正確立。
在三角函數中,有一些特殊角,例如30°、45°、60°,這些角的三角函數值為簡單單項式,計算中可以直接求出具體的值。
這些函數的值參見下表格:
| 角度 | 0° | 15° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° |
| 弧度 | π/12 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 3π/2 | |
| sin值 | [(√6)-(√2)]/4 | 1/2 | (√2)/2 | (√3)/2 | 1 | (√3)/2 | (√2)/2 | 1/2 | -1 | ||
| cos值 | 1 | [(√6)+(√2)]/4 | (√3)/2 | (√2)/2 | 1/2 | -1/2 | -(√2)/2 | -(√3)/2 | -1 | ||
| tan值 | 2-√3 | (√3)/3 | 1 | √3 | ∅ | -√3 | -1 | -(√3)/3 | ∅ | ||
| cot值 | ∅ | 2+√3 | √3 | 1 | √3)/3 | -(√3)/3 | -1 | -√3 | ∅ |
| 函數 | 對稱軸 | 對稱中心 |
|---|---|---|
y=sin x 正弦函數 | x=kπ+π/2(k∈Z) | (kπ,0)(k∈Z) |
y=cos x 餘弦函數 | x=kπ(k∈Z) | (kπ+π/2,0)(k∈Z) |
y=tan x 正切函數 | 無 | (kπ/2,0)(k∈Z) |
y=cot x 餘切函數 | 無 | (kπ/2,0)(k∈Z) |
y=sec x 正割函數 | x=kπ(k∈Z) | (kπ+π/2,0)(k∈Z) |
y=csc x 餘割函數 | x=kπ+π/2(k∈Z) | (kπ,0)(k∈Z) |
最小正周期
如果一個函數f(x)的所有周期中存在一個最小的正數,那麼這個最小的正數就叫做f(x)的最小正周期(minimal positive period)。例如,正弦函數的最小正周期是2π。
正數函數
對於正弦函數y=sin x,自變數x只要並且至少增加到x+2π時,函數值才能重複取得。正弦函數和餘弦函數的最小正周期是2π。
公式內容
| 三角函數十組誘導公式 | |
| 公式一 | 公式二 |
sin(2kπ+α)=sin α cos(2kπ+α)=cos α tan(2kπ+α)=tan α cot(2kπ+α)=cot α sec(2kπ+α)=sec α csc(2kπ+α)=csc α | sin(π+α)=-sin α cos(π+α)=-cos α tan(π+α)=tan α cot(π+α)=cot α sec(π+α)=-sec α csc(π+α)=-csc α |
| 公式三 | 公式四 |
sin(-α)=-sin α cos(-α)=cos α tan(-α)=-tan α cot(-α)=-cot α sec(-α)=sec α csc(-α)=-csc α | sin(π-α)=sin α cos(π-α)=-cos α tan(π-α)=-tan α cot(π-α)=-cot α sec(π-α)=-sec α csc(π-α)=csc α |
| 公式五 | 公式六 |
sin(α-π)=-sin α cos(α-π)=-cos α tan(α-π)=tan α cot(α-π)=cot α sec(α-π)=-sec α csc(α-π)=-csc α | sin(2π-α)=-sin α cos(2π-α)=cos α tan(2π-α)=-tan α cot(2π-α)=-cot α sec(2π-α)=sec α csc(2π-α)=-csc α |
| 公式七 | 公式八 |
sin(π/2+α)=cosα cos(π/2+α)=−sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sec(π/2+α)=-cscα csc(π/2+α)=secα | sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sec(π/2-α)=cscα csc(π/2-α)=secα |
| 公式九 | 公式十 |
sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sec(3π/2+α)=cscα csc(3π/2+α)=-secα | sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα sec(3π/2-α)=-cscα csc(3π/2-α)=-secα |
推導方法
定名法則
90°的奇數倍+α的三角函數,其絕對值與α三角函數的絕對值互為余函數。90°的偶數倍+α的三角函數與α的三角函數絕對值相同。也就是“奇余偶同,奇變偶不變”。
定號法則
將α看做銳角(注意是“看做”),按所得的角的象限,取三角函數的符號。也就是“象限定號,符號看象限”(或為“奇變偶不變,符號看象限”)。
在Kπ/2中如果K為偶數時函數名不變,若為奇數時函數名變為相反的函數名。正負號看原函數中α所在象限的正負號。關於正負號有個口訣;一全正,二正弦,三兩切,四餘弦,即第一象限全部為正,第二象限角,正弦為正,第三象限,正切和餘切為正,第四象限,餘弦為正。或簡寫為“ASTC”,即“all”“sin”“tan+cot”“cos”依次為正。還可簡記為:sin上cos右tan/cot對角,即sin的正值都在x軸上方,cos的正值都在y軸右方,tan/cot 的正值斜著。
比如:90°+α。定名:90°是90°的奇數倍,所以應取余函數;定號:將α看做銳角,那麼90°+α是第二象限角,第二象限角的正弦為正,餘弦為負。所以sin(90°+α)=cosα , cos(90°+α)=-sinα 這個非常神奇,屢試不爽~
還有一個口訣“縱變橫不變,符號看象限”,例如:sin(90°+α),90°的終邊在縱軸上,所以函數名變為相反的函數名,即cos,所以sin(90°+α)=cosα。
兩角和與差
取直角坐標系,作單位圓;取一點A,連接OA,與X軸的夾角為α; 取一點B,連接OB,與X軸的夾角為β, 則OA與OB的夾角即為α-β
∵A(cosα,sinα),B (cosβ,sinβ),O(0,0)
∴OA=(cosα,sinα),OB=(cosβ,sinβ)(向量)
∴OA·OB=|OA| |OB| cos (α-β) =cos α cos β + sin α sin β
∵|OA| = |OB| = 1
∴cos(α-β)=cosαcosβ+sinαsinβ
取β=-β,可得cos(α+β)=cosαcosβ-sinαsinβ
以上內容來自:
和差化積
積化和差
三倍角公式
sin(3α) = 3sinα-4sinα = 4sinα·sin(60°+α)sin(60°-α)
cos(3α) = 4cosα-3cosα = 4cosα·cos(60°+α)cos(60°-α)
tan(3α) = (3tanα-tanα)/(1-3tan²α) = tanαtan(π/3+α)tan(π/3-α)
cot(3α)=(cotα-3cotα)/(3cotα-1)
n倍角公式
根據棣莫弗公式(cosθ+isinθ)^n=cosnθ+isinnθ
將左邊用二項式定理展開分別整理實部和虛部可以得到下面兩組公式
sin(nα)=ncosα·sinα-C(n,3)cosα·sinα+C(n,5)cosα·sinα-…
cos(nα)=cosα-C(n,2)cosα·sinα+C(n,4)cosα·sinα
半形公式
公式:
(其中φ滿足 , )
sina=[2tan(a/2)]/[1+tan²(a/2)]
cosa=[1-tan²(a/2)]/[1+tan²(a/2)]
tana=[2tan(a/2)]/[1-tan²(a/2)]
降冪公式
sin²α=[1-cos(2α)]/2
cos²α=[1+cos(2α)]/2
tan²α=[1-cos(2α)]/[1+cos(2α)]
三角和
sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγ
cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγ
tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)÷(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)
冪級數
它們的各項都是正整數冪的冪函數, 其中c0,c1,c2,...cn...及a都是常數, 這種級數稱為冪級數。
泰勒展開式又叫冪級數展開法
實用冪級數:
e = 1+x+x/2!+x/3!+…+x/n!+…,x∈R
sin x = x-x/3!+x/5!-…+(-1)x/(2k-1)!+…, x∈R
cos x = 1-x/2!+x/4!-…+(-1)x/(2k)!+…, x∈R
arcsin x = x + x/(2×3) + (1×3)x/(2×4×5) + (1×3×5)x/(2×4×6×7)…+(2k-1)!!×x/(2k!!×(2k+1))+…, x∈(-1,1)(!!表示雙階乘)
arccos x = π/2 -[x + x/(2×3) + (1×3)x/(2×4×5) + (1×3×5)x/(2×4×6×7)……], x∈(-1,1)
arctan x = x - x/3 + x/5 -…, x∈(-∞,1)
sinh x = x+x/3!+x^/5!+…+x/(2k-1)!+…, x∈R
cosh x = 1+x/2!+x^/4!+…+x/(2k)!+…, x∈R
arcsinh x =x - x/(2×3) + (1×3)x/(2×4×5) -(1×3×5)x/(2×4×6×7)…, x∈(-1,1)
arctanh x = x + x/3 + x/5 + …, x∈(-1,1)
在解初等三角函數時,只需記住公式便可輕鬆作答,在競賽中,往往會用到與圖像結合的方法求三角函數值、三角函數不等式、面積等等。
傅里葉級數
傅里葉級數
傅里葉級數又稱三角級數
f(x)=a0/2+∑(n=0..∞) (ancosnx+bnsinnx)
a0=1/π∫(π..-π) (f(x))dx
an=1/π∫(π..-π) (f(x)cosnx)dx
bn=1/π∫(π..-π) (f(x)sinnx)dx
定義域和值域
sin(x),cos(x)的定義域為R,值域為[-1,1]。
tan(x)的定義域為x不等於π/2+kπ(k∈Z),值域為R。
cot(x)的定義域為x不等於kπ(k∈Z),值域為R。
y=a·sin(x)+b·cos(x)+c 的值域為 [ c-√(a²;+b²;) , c+√(a²;+b²;)]
周期T=2π/ω
函數圖象畫法
以y=sinx的圖像為例,得到y=Asin(ωx+φ)的圖像:
方法一:
y=sinx→【左移(φ>0)/右移(φ<0) ∣∣∣φ∣個單位】 →y=sin(x+φ)→【縱坐標不變,橫坐標伸縮到原來的(1/ω)】→y=sin(ωx+φ)→【縱坐標變為原來的A倍(伸長[A>1] / 縮短[0
方法二:
y=sinx→【縱坐標不變,橫坐標伸縮到原來的(1/ω)】→y=sinωx→【左移(φ>0)/右移(φ<0)∣φ∣/ω 個單位】→y=sin(ωx+φ) →【縱坐標變為原來的A倍(伸長[A>1] / 縮短[0
導數
三角函數圖象
| y=sinx | y'=cosx |
| y=cosx | y'=-sinx |
| y=tanx | y'=1/cos²x =sec²x |
| y=cotx | y'= -1/sin²x= - csc²x |
| y=secx | y'=secxtanx |
| y=cscx | y'=-cscxcotx |
| y=arcsinx | y'=1/√(1-x²) |
| y=arccosx | y'= -1/√(1-x²) |
| y=arctanx | y'=1/(1+x²) |
| y=arccotx | y'= -1/(1+x²) |
倍半形規律
如果角a的餘弦值為1/2,那麼a/2的餘弦值為√3/2.
三角函數的反函數
三角函數的反函數,是多值函數。它們是反正弦arcsin x,反餘弦arccos x,反正切arctan x,反餘切arccot x等,各自表示其正弦、餘弦、正切、餘切、正割、餘割為x的角。為限制反三角函數為單值函數,將反正弦函數的值y限在y=-π/2≤y≤π/2,將y為反正弦函數的主值,記為y=arcsin x;相應地,反餘弦函數y=arccos x的主值限在0≤y≤π;反正切函數y=arctan x的主值限在-π/2
反三角函數實際上並不能叫做函數,因為它並不滿足一個自變數對應一個函數值的要求,其圖像與其原函數關於函數y=x對稱。其概念首先由歐拉提出,並且首先使用了arc+函數名的形式表示反三角函數,而不是f-1(x).
反三角函數主要是三個:
y=arcsin(x),定義域[-1,1],值域[-π/2,π/2],圖象用紅色線條;
y=arccos(x),定義域[-1,1],值域[0,π],圖象用藍色線條;
y=arctan(x),定義域(-∞,+∞),值域(-π/2,π/2),圖象用綠色線條;
sinarcsin(x)=x,定義域[-1,1],值域 [-π/2,π/2]
證明方法如下:設arcsin(x)=y,則sin(y)=x ,將這兩個式子代入上式即可得
其他幾個用類似方法可得。
高等代數中三角函數的指數表示(由泰勒級數易得):
泰勒展開有無窮級數,e=exp(z)=1+z/1!+z/2!+z/3!+z/4!+…+z/n!+… ≦
此時三角函數定義域已推廣至整個複數集。
·三角函數作為微分方程的解:
對於微分方程組 y=-y'';y=y'''',有通解Q,可證明
Q=Asinx+Bcosx,因此也可以從此出發定義三角函數。
補充:由相應的指數表示我們可以定義一種類似的函數--雙曲函數,其擁有很多與三角函數的類似的性質,二者相映成趣。
(1)對於z為實數y來說,複數域內正餘弦函數的性質與通常所說的正餘弦函數性質是一樣的。
(2)複數域內正餘弦函數在z平面是解析的。
(3)在複數域內不能再斷言|sinz|≦1,|cosz|≦1。
(4)sinz、cosz分別為奇函數,偶函數,且以2π為周期。
複數三角函數:
sin(a+bi)=sinacosbi+sinbicosa
=sinachb+ishbcosa
cos(a-bi)=cosacosbi+sinbisina
=cosachb+ishbsina
tan(a+bi)=sin(a+bi)/cos(a+bi)
cot(a+bi)=cos(a+bi)/sin(a+bi)
sec(a+bi)=1/cos(a+bi)
csc(a+bi)=1/sin(a+bi)
解釋
正、餘弦定理
三角函數,正如其名稱那樣,在三角學中是十分重要的,主要是因為正弦定理與餘弦定理。
同時在解決物理中的力學問題時也很重要,主要在於力與力之間的轉換,並列出平衡方程。
正弦定理
對於邊長為a,b和c而相應角為A,B和C的三角形,有:
sinA / a = sinB / b = sinC/c
也可表示為:
a/sinA=b/sinB=c/sinC=2R
變形:a=2RsinA,b=2RsinB,c=2RsinC
其中R是三角形的外接圓半徑。
它可以通過把三角形分為兩個直角三角形並使用上述正弦的定義來證明。在這個定理中出現的公共數 (sinA)/a是通過A,B和C三點的圓的直徑的倒數。正弦定理用於在一個三角形中(1)已知兩個角和一個邊求未知邊和角(2)已知兩邊及其一邊的對角求其他角和邊的問題。這是三角測量中常見情況。
三角函數正弦定理可用於求得三角形的面積:
S=1/2absinC=1/2bcsinA=1/2acsinB
餘弦定理
對於邊長為a、b、c而相應角為A、B、C的三角形,有:
a² = b² + c²- 2bc·cosA
b² = a² + c² - 2ac·cosB
c² = a² + b² - 2ab·cosC
也可表示為:
cosC=(a² +b² -c²)/ 2ab
cosB=(a² +c² -b²)/ 2ac
cosA=(c² +b² -a²)/ 2bc
這個定理也可以通過把三角形分為兩個直角三角形來證明。餘弦定理用於在一個三角形的兩個邊和一個角已知時確定未知的數據。
如果這個角不是兩條邊的夾角,那麼三角形可能不是唯一的(邊-邊-角)。要小心餘弦定理的這種歧義情況。
延伸定理:第一餘弦定理(任意三角形射影定理)
設△ABC的三邊是a、b、c,它們所對的角分別是A、B、C,則有
a=b·cos C+c·cos B, b=c·cos A+a·cos C, c=a·cos B+b·cos A
對於邊長為a,b和c而相應角為A,B和C的三角形,有:
廣義射影定理
三角形中任意一邊等於其他兩邊以及對應角餘弦的交叉乘積的和,即a=c cosB + b cosC
三角恆等式
對於任意非直角三角形中,如三角形ABC,總有tanA+tanB+tanC=tanAtanBtanC
證明:
已知(A+B)=(π-C)
所以tan(A+B)=tan(π-C)
則(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)
整理可得
tanA+tanB+tanC=tanAtanBtanC
類似地,我們同樣也可以求證:當α+β+γ=nπ(n∈Z)時,總有tanα+tanβ+tanγ=tanαtanβtanγ。
正弦函數
主詞條:正弦函數。
格式:sin(θ)。
作用:在直角三角形中,將大小為θ(單位為弧度)的角對邊長度比斜邊長度的比值求出,函數值為上述比的比值,也是csc(θ)的倒數。
函數圖像:波形曲線。
值域:-1~1。
餘弦函數
主詞條:餘弦函數。
格式:cos(θ)。
作用:在直角三角形中,將大小為(單位為弧度)的角鄰邊長度比斜邊長度的比值求出,函數值為上述比的比值,也是sec(θ)的倒數。
函數圖像:波形曲線。
值域:-1~1。
正切函數
主詞條:正切函數。
格式:tan(θ)。
正切函數圖像
作用:在直角三角形中,將大小為θ(單位為弧度)的角對邊長度比鄰邊長度的比值求出,函數值為上述比的比值,也是cot(θ)的倒數。
函數圖像:右圖平面直角坐標系反映。
值域:-∞~∞。
主詞條:餘切函數。
格式:cot(θ)。
餘切函數圖像
作用:在直角三角形中,將大小為θ(單位為弧度)的角鄰邊長度比對邊長度的比值求出,函數值為上述比的比值,也是tan(θ)的倒數。
函數圖像:右圖平面直角坐標系反映。
值域:-∞~∞。
主詞條:正割函數。
格式:sec(θ)。
正割函數圖像
作用:在直角三角形中,將斜邊長度比大小為θ(單位為弧度)的角鄰邊長度的比值求出,函數值為上述比的比值,也是cos(θ)的倒數。
函數圖像:右圖平面直角坐標系反映。
值域:≥1或≤-1。
餘割函數
主詞條:餘割函數。
餘割函數圖像
格式:csc(θ)。
作用:在直角三角形中,將斜邊長度比大小為θ(單位為弧度)的角對邊長度的比值求出,函數值為上述比的比值,也是sin(θ)的倒數。
函數圖像:右圖平面直角坐標系反映。
值域:≥1或≤-1。
正矢函數
主詞條:正矢函數。
格式:versin(θ)。
作用:在直角三角形中,求出1-cos(θ)(括弧中填的是大小為θ(單位為弧度)的角的大小),函數值為1-cos(θ)。
值域:0~2。
余矢函數
主詞條:余矢函數。
格式:coversin(θ)。
作用:在直角三角形中,求出1-sin(θ)(括弧中填的是大小為θ(單位為弧度)的角的大小),函數值為1-sin(θ)。
值域:0~2。
半正矢函數
主詞條:半正矢函數。
格式:haversin(θ)。
作用:在直角三角形中,求出[1-cos(θ)]÷2(括弧中填的是大小為θ(單位為弧度)的角的大小),函數值為[1-sin(θ)]÷2。
值域:0~1。
半余矢函數
主詞條:半余矢函數。
格式:hacoversin(θ)。
作用:在直角三角形中,求出[1-sin(θ)]÷2(括弧中填的是大小為θ(單位為弧度)的角的大小),函數值為[1-sin(θ)]÷2。
值域:0~1。
外正割函數
主詞條:外正割函數。
格式:exsec(θ)。
作用:在直角三角形中,求出sec(θ)-1(括弧中填的是大小為θ(單位為弧度)的角的大小),函數值為sec(θ)-1。
外餘割函數
主詞條:外餘割函數。
格式:excsc(θ)。
作用:在直角三角形中,求出csc(θ)-1(括弧中填的是大小為θ(單位為弧度)的角的大小),函數值為csc(θ)-1。
三角函數是函數,象限符號坐標註。函數圖像單位圓,周期奇偶增減現。
同角關係很重要,化簡證明都需要。正六邊形頂點處,從上到下弦切割;
中心記上數字一,連結頂點三角形。向下三角平方和,倒數關係是對角,
頂點任意一函數,等於後面兩根除。誘導公式就是好,負化正後大化小,
變成銳角好查表,化簡證明少不了。二的一半整數倍,奇數化余偶不變,
將其後者視銳角,符號原來函數判。兩角和的餘弦值,化為單角好求值,
餘弦積減正弦積,換角變形眾公式。和差化積須同名,互餘角度變名稱。
計算證明角先行,注意結構函數名,保持基本量不變,繁難向著簡易變。
逆反原則作指導,升冪降次和差積。條件等式的證明,方程思想指路明。
萬能公式不一般,化為有理式居先。公式順用和逆用,變形運用加巧用;
一加餘弦想餘弦,一減餘弦想正弦,冪升一次角減半,升冪降次它為范;
三角函數反函數,實質就是求角度,先求三角函數值,再判角取值範圍;
利用直角三角形,形象直觀好換名,簡單三角的方程,化為最簡求解集。
目錄