多複變函數論
多複變函數論
數學中研究多個復變數的全純函數的性質和結構的分支學科,有時也稱多複分析。
目錄
它形成較晚,但發展迅速。它雖然有著經典的單複變函數的淵源,但由於其特有的困難和複雜性,在研究的重點和方法上,都和單複變函數論(見複變函數論)有顯著的區別。因為多復變全純函數的性質在很大程度上由定義區域的幾何和拓撲性質所制約,因此,其研究的重點經歷了一個由局部性質到整體性質的逐步的轉移。它廣泛地使用著微分幾何學、代數幾何、李群、拓撲學、微分方程等相鄰學科中的概念和方法,不斷地開闢前進的道路,更新和拓展研究的內容和領域。如果說各學科的相互滲透和影響日益廣泛是近代數學的特徵,那麼對多複變函數論而言,這一特點尤為顯著。
歷史發展 多複變函數論的研究,早在單複變函數論的(G.F.)B.黎曼和K.(T.W.)外爾斯特拉斯時代就已經零散地開始了。但真正標誌著多複變函數論這一學科創立的,是19世紀末和20世紀初(J.-)H.龐加萊、P.庫辛、F.M.哈托格斯等人的工作。他們的研究揭示了多復變全純函數本質上的獨特性。在這當中,庫辛提出的關於全純函數整體性質的兩個以他命名的問題以及E.E.列維提出的擬凸域和全純域是否等價的問題,更有著深遠的影響,長時間成為多複變函數論發展的一個推動因素。20世紀30年代以前,雖然出現過K.萊因哈特關於解析自同構群、S.伯格曼關於核函數和度量等重要工作,但整個說來,多複變函數論處於相對沉寂的時期。從30年代開始,多復變的研究迎來了初步繁榮。這一時期中陸續出現了H.嘉當關於全純自同構的惟一性定理、有界域全純自同構群的李群性質以及全純域與全純凸的等價性的嘉當-蘇倫定理等突出成果。特別是從1936年開始,日本數學家岡潔對庫辛問題、列維問題、逼近問題等多復變的中心問題進行了長期、系統而富有成效的研究,終於在50年代對上述諸問題給出了解答。他的這一系列工作對以後年代的多復變的發展有著重大的影響。50年代以後,和近代數學的綜合化、抽象化的總潮流相一致,在多複變函數論中用拓撲方法和幾何方法研究全純函數的整體性質的趨勢變得越來越明顯。由J.勒雷引進拓撲學的層及其上同調的概念被迅速而成功地用於多復變。這一概念和H.嘉當早先關於全純函數理想論的研究以及岡潔的思想結合,導致了凝聚解析層理論的建立。與此同時,復空間和施泰因流形的概念也應運而生。H.嘉當和J.P.塞爾系統地應用凝聚層理論建立了施泰因流形的基本定理。此後不久,H.格勞爾特解決了複流形的列維問題,他和R.雷默特、施泰因等人還大大發展了復空間的理論。整個50年代無疑是多復變發展的黃金時代。
另一方面,近代微分幾何與複分析的相互溶合也在不斷加快步伐。1913年,(C.H.)H.外爾的黎曼曲面理論導致了複流形概念的建立。É.(-J.)嘉當的外微分式與拓撲的結合產生了G.- W.德·拉姆的上同調理論。以此為基礎,W.V.D.霍奇將黎曼曲面上的調和函數理論推廣到高維的緊緻複流形,證明了緊複流形的基本定理──霍奇定理。40年代以後,與微分幾何中的博赫納技巧相結合,霍奇理論又由小平邦彥所發展和完善。60年代,博赫納-小平邦彥方法又進而推廣到非緊的帶邊界的複流形,發展成為近代多複分析的一個有力工具:扺問題的L2估計。
多複變函數論中具有重要意義的第三方面進展是C.L.西格爾在年間建立的多複變函數的自守函數論。50年代以後,由於A.賽爾伯格、R.朗蘭茲、И.М.蓋爾范德等人的工作,揭示了它與代數數論、李群的無窮維表示、代數幾何等眾多學科的內在聯繫,而日益成為目前極為活躍而且引人注目的近代數學領域之一。
多復變數的全純函數 以Cn表示n維復歐氏空間,其中的點,每一zi是一複數。設Ω是Cn中的一個開集,復值函數ƒ(z)稱為在Ω上是全純的,如果下列條件滿足:對於Ω中的任何點,ƒ(z)在z0附近可以表為下述形式的收斂冪級數:
。
從形式上看,多復變全純函數是單復變全純函數的推廣。事實上兩者的基本性質確有許多相似之處。例如:
① 對每個分量滿足柯西-黎曼方程,即
,
。
③ 極大模原理 設ƒ是在區域Ω上定義的全純函數,如果在某一內點α,對於所有的成立,那麼ƒ(z)恆為常數。
當然,構成多復變數全純函數研究內容的主要不是這些共同的性質,而是它的獨特性質。這方面,下述兩個問題具有特別的重要性,它們都導致了長期而且大量的研究:
① 解析開拓 F.M.哈托格斯發現,設Ω是中一個域,K是Ω中緊集,Ω-K連通,那麼任何在Ω-K全純的函數都可以開拓到整個Ω,成為Ω上的全純函數。這種性質是單復變全純函數所決不具有的。與這種哈托格斯現象有關的研究構成了多複變函數論的基本內容之一。
② 零點的局部性狀 單復變中全純函數的零點是孤立的。多復變全純函數的零點,即使以最簡單的例子來看也已經不再是孤立的。有限個全純函數的公共零點的集合稱為解析集。解析集的結構及多復變全純函數在其零點附近的性狀較之單復變的相應情況要複雜得多。討論這一理論的基礎是外爾斯特拉斯預備定理。記Cn的原點為O,以θn表示所有在O的某一鄰域全純的函數組成的環。則外爾斯特拉斯預備定理斷言:任何一個非零元,都存在一組坐標以O為原點,使並且ƒ等於θn中一個可逆元與一個示性多項式的乘積,這裡的示性多項式形狀為:
式中
。
這一定理的作用在於在一定程度上將全純函數的問題化歸多項式的問題。從它出發可以證明,θn是諾特環(即其中的任何理想都具有限基)。不僅如此,著名的對多項式環而言的希爾伯特零點定理對環θn也成立,由此可以獲得對解析集局部結構的較清晰的了解。利用這些結果,如果把θn看成Cn上全純函數的芽生成的層,岡潔證明了多複變函數論中具基本重要性的定理之一:θn是凝聚層。
全純域與列維問題 如果Ω是複平面C 中的一個域,掍是另一個包含Ω而較大的域,那麼總是存在在Ω中全純而不能全純開拓到掍的函數(只要任取在掍中而不在Ω的一點α,考慮函數即可)。這種現象在多複變函數中不再成立。
哈托格斯發現,Cn中有些域Ω具有這樣的性質:總是存在一個包含它的更大的域掍,使任何在Ω中全純的函數都可以全純開拓到掍中去。由此,自然提出這樣的問題:如何刻畫那些不具備以上開拓性質的域?這一問題的精確提法就是全純域的概念。域Ω嶅Cn稱為全純域,如果不存在更大的包含Ω的域掍,使任何Ω上的全純函數都可以全純開拓到掍上。
全純域的刻畫在多複變函數論的歷史發展中長時期處於主導的地位。這方面的第一個重要結果是H.嘉當和蘇倫給出的:Ω是全純域的充分必要條件是,對於Ω中的任何緊子集K,集合上的全純函數也是Ω中的緊子集。這種性質稱為全純凸性。嘉當-蘇倫定理是用全純凸來刻畫全純域,但更自然的是能給出域的幾何刻畫。進一步的研究表明,域的全純性和它的某種凸性有關,在這點上,通常的歐氏空間中的凸域具有一定的借鑒作用。歐氏空間Rn中的凸域(一域稱為凸的,如果連接其中任何兩點的線段也整個在該域之中),其充要條件是該域上存在一個二階連續可微的函數u,滿足:當x→域的邊界時,u(x)→;並且對任何實數有。以此為背景,哈托格斯與列維引進了擬凸域的概念。為了說明這一概念,稱定義於Ω上的二階連續可微的函數u(z)是窮竭的,如果當 z→邊界時,是多重次調和的,如果對於任何複數它在Ω中任意點都滿足。於是有定義:具有窮竭的多重次調和函數的域,稱為擬凸域。
根據嘉當-蘇倫定理,不難證明全純域是擬凸域。困難的、長期未決的是其反面:擬凸域是否一定是全純域?這就是所謂列維問題。列維問題的肯定性解答當n=2時由岡潔最先給出(1942),其一般情況分別由岡潔、伯格曼和F.諾蓋獨立證明(1953~1954)。列維問題的解決引出了大量的,至今仍很活躍的推廣性研究。其中,最具重要性的是格勞爾特的工作。它涉及的是對複流形而言的列維問題。全純域在複流形中的類似概念稱為施泰因流形。簡單地說,施泰因流形是這樣的複流形:它是全純凸的,它上面具有足夠多的全純函數以致可以區別不同的點,並給出每一點的局部坐標。於是,對複流形而言的列維問題就變成了:什麼樣的複流形是施泰因流形?格勞爾特對此的回答(1958)是:容許光滑的、窮竭的強多次調和函數存在的複流形是施泰因流形。
解決列維問題的另一種方法是扺運算元的L2估計,它在60年代中期得到了迅速的發展。事實上,包括列維問題在內的許多函數論問題,如下面要提到的庫辛問題與龍格型定理及復向量叢上的嘉當定理等,都可以化歸為扺問題:證明一般的(即可能是非齊次的)柯西-黎曼方程扺(滿足條件扺)解的存在性與正則性。從一般的柯西-黎曼方程,自然地得出由微分形式的希爾伯特空間到微分形式的希爾伯特空間的微分運算元,即扺運算元。它及它的共軛運算元扺都是線性的稠定的閉運算元。1950年,D.C.斯潘塞在企圖將霍奇理論推廣到開流形時,首先提出了著名的扺-紐曼問題:證明方程的解的存在性與正則性。這是研究扺問題十分有效的手段。因為若加上條件扺,在知道了這個方程的解φ以後,就可以將扺問題的解表示成u=扺φ。通過一系列先驗估計,J.J.科恩從1963年開始,對於幾類重要的擬凸流形,特別是強擬凸流形,徹底解決了扺-紐曼問題。1965年,L.赫爾曼德爾在微分形式的希爾伯特空間引入權函數來直接研究扺問題,取得了很大成功。權函數的引入避開了扺-紐曼問題中處理解的邊界正則性的難點,使得對於一般的施泰因流形直接得到了內部存在性與正則性。因此在某種意義上,它比 扺-紐曼問題更適於多複變函數論的應用。同時,扺運算元理論的發展,不僅為複流形,特別是施泰因流形的研究提供了強有力的工具,而且促進了擬微分運算元理論的誕生及超定微分方程等分支的發展。
庫辛問題與龍格型定理 推動多複變函數論發展的內在邏輯之一是尋求單複變函數論中的哪些基本事實可以推廣到多復變中來。還在多復變發展的早期,法國數學家庫辛就提出了單復變中兩個經典定理(外爾斯特拉斯定理和米塔-列夫勒定理)如何推廣的問題,這就是庫辛問題。單復變中的外爾斯特拉斯定理是說,對C中域Ω而言,永遠存在這樣的全純函數,它以指定的點集(當然假定是離散的)為自己的零點集,並且重數等於指定的重數。米塔-列夫勒定理說,對C中域Ω而言,永遠存在這樣的亞純函數,它以指定的點集為自己的極點集,並且重數等於指定的重數。為了說明庫辛問題,先解釋什麼是多復變的亞純函數。定義於區域中的復值函數如果它在任何點的局部都可以表為兩個全純函數之商並且分母不恆為零,這樣的函數稱為亞純函數。庫辛第一問題:{Uα}是區域Ω的一組開集覆蓋,對每一α,有一定義於Uα的亞純函數ƒα滿足,當時,ƒα-ƒβ是Uα∩Uβ上的全純函數(換言之,ƒα和ƒβ在定義域相交的部分有相同的極點)。是否存在整個定義於Ω的亞純函數ƒ,使對每一α,在Uα上是全純的?庫辛第二問題:設{Uα}是域Ω的開集覆蓋。如果對每一Uα,有一定義於其中的全純函數ƒα滿足,如,是上不取零值的全純函數(即ƒα和ƒβ在定義域相交的部分有相同的零點)。是否存在一個整體定義於Ω的全純函數ƒ,使對每一α,ƒ/ƒα在Uα上為一不取零值的全純函數?對庫辛問題的解決作出最主要貢獻的是岡潔。它們的解決一方面與全純域的理論有關,一方面與層及層的上同調理論有關。岡潔對庫辛問題的解答如下:如果Ω是全純域,庫辛第一問題是永遠可解的。但即使是全純域,庫辛第二問題並不一定永遠可解,它的可解性還依賴於一定的拓撲條件。其可解的一個充分必要條件是,它在連續函數的範疇內可解,即如果能找到一個定義於Ω的連續函數g,使對每一α,在Uα上為一不取零值的連續函數。上述對庫辛問題的解答揭示了一個在多復變研究中具有指導性的哲理:許多涉及全純性範疇的問題的可解性常常依賴於連續性範疇的相應問題的可解性,雖然這並不是業已證明的原理,但卻是經常有效的。
龍格型定理研究的是全純函數的逼近。單復變中最簡單的龍格定理如下:如K是複平面C中一個有界閉集,ƒ是一定義於K的某鄰域的全純函數,那麼ƒ一定可以用多項式一致逼近。注意到多項式可以一致逼近任意整函數,而整函數就是定義於C的全體全純函數。因此多復變中的龍格定理的正確提法應該是:如果Ω是全純域,K是Ω中的有界閉集,並且凬Ω中全純函數g}如果ƒ 是定義於K 的某鄰域的全純函數,那麼ƒ一定可以用定義於Ω的全純函數一致逼近。這種類型的龍格定理是由A.韋伊及岡潔證明的。
複流形和復向量叢 正如單復變全純函數的研究必然導致黎曼曲面的概念一樣,在多復變中複流形的引進同樣是不可避免的。粗略地說,複流形是這樣的拓撲空間,其每點的局部和Cn中的開集相同。精確地說,滿足以下條件的拓撲空間M稱為n維複流形:M是一個豪斯多夫拓撲空間。{Uk}是M的一族開集覆蓋。對每一k,存在Uk與Cn中某開集Ωk的一個雙方一一的連續映射φk,滿足:①M的每一點都至少屬於一個Uk,②如果,則映射 是全純的。在這種定義下,可以將M中的Uk和Cn中的Ωk等同起來,而將Ωk中點的坐標稱為Uk中相應點的局部坐標,於是條件②表明,不同局部坐標之間的關係是全純的。由此可推知,定義於M上的復值函數如果對某一局部坐標是全純的,那麼對任何其他局部坐標也都是全純的。因此,複流形上全純函數的定義是有意義的。
複流形按其是否緊緻,分為緊複流形和非緊複流形兩大類。相對地說,緊複流形的研究成果要豐富得多。複流形的各方面:幾何、拓撲、函數論及其相互關係都各有獨自而又相互交叉的研究,構成了近年來蓬勃興起的新分支大範圍分析(見大範圍變分法)的重要內容之一。
在多複變函數論中研究得最深入的非緊複流形是施泰因流形。設有複流形M,滿足條件:①全純凸性,即對於M中的任何緊子集K,集合
也是M中的緊子集;②它有足夠多的全純函數,即對於M中任何二個不同的點x1、x2都存在M上的全純函數ƒ,使ƒ(x1)≠ƒ(x2);③對於任何x∈M,都存在M上的全純函數ƒ1,ƒ2,…,ƒn,使ƒ1,ƒ2,…,ƒn可作為x附近的局部坐標。這時M稱為施泰因流形。施泰因流形的函數論刻畫是格勞爾特給出的,而其幾何特徵則是由E.畢曉普、R.納拉西姆漢給出的:若複流形是施泰因流形則它可嵌入某一CN中成為後者的閉子複流形。
幾何上最簡單而常見的複流形是被稱為凱勒流形的一類。凱勒流形,簡單地說,滿足以下條件:對流形上的任何一點,可以選擇這樣的局部坐標z1,z2,…,zn,在此局部坐標下其度量可表為,。換言之,凱勒流形上的度量如果和歐氏空間Cn的度量比較起來,兩者的密合是二階的。對緊緻凱勒流形的幾何和拓撲性質人們已經進行了大量的研究。主題之一是,利用它的幾何性質(由曲率表徵)來獲取其拓撲信息(由同調群表徵)。這方面的基本結果,所謂消沒定理,是小平邦彥得到的。例如,其中一個典型結果是,緊緻凱勒流形M,如果其凱勒度量下的里奇曲率為正,則對任何正整數q,都有,這裡是M上取值於(0,q)形式芽層的上同調群。
在複流形的研究中,以流形的切空間為背景發展起來的復向量叢的概念是一個重要的概念。複流形M上的一個復向量叢,直觀地說,就是M上每一點都“粘附”上一個有限維的復向量空間,這種“粘附”滿足以下規則:對任何x∈M,以Kx表示在x點粘附的復向量空間(稱為x上的纖維)。因為M是複流形,x可以有不同的局部坐標領域U和V,x∈U∩V。U 的局部坐標和V的局部坐標之間的關係是全純的。Kx中同一向量的坐標在U和V下有不同的表示,這兩個表示之間的關係由一個m×M矩陣(m=Kx的維數)給出,這個矩陣稱為聯接函數。如果聯接函數對局部坐標來說是全純的,並且其行列式在U∩V中恆不為零。這樣所得到的M連同其各點的纖維組成的總空間E 稱為M上的復向量叢。各點纖維Kx的維數稱為此向量叢的秩。不難證明,復向量叢本身也是一個複流形。如果復向量叢的秩為1,這樣的叢稱為複線叢。
對於複流形M上的復向量叢K,可以考慮取值於K的無窮次可微的(p,q)微分形式。這種形式就局部來說可以寫成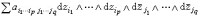 ,其中(x)是屬於x的纖維Kx中的向量,並且當x變動時是x的無窮次可微函數。通過它,可以定義M上的取值於向量叢K的同調群H(p,q)(M,K)。
,其中(x)是屬於x的纖維Kx中的向量,並且當x變動時是x的無窮次可微函數。通過它,可以定義M上的取值於向量叢K的同調群H(p,q)(M,K)。
多複變函數論
對於緊緻複流形上的復向量叢,基本的結果是霍奇定理,該定理斷言:上同調群H(p,q)(M,K)是有限維的,並且其維數等於取值於K的(p,q)調和形式的線性無關數。這個定理由於將流形上的分析結構與拓撲結構聯繫起來,而成為複流形理論的基石之一。
關於緊複流形的另一重要結果是小平邦彥的嵌入定理。它斷言,緊複流形如果具有一正的線叢,那麼它就可以嵌入復射影空間而成為代數流形,即由有限個多項式零點所組成。
層及以層為係數的上同調群 層和以層為係數的上同調群的概念最早是法國數學家勒雷由於拓撲的需要而引進的,後由於韋伊、H.嘉當、J.P.塞爾等人的改進,成了近代多複分析及代數幾何的基本工具。它是研究全純函數的局部性質過渡到整體性質的有力方法。也是迄今為止處理比複流形更廣的對象──復空間的最有效方法。所謂復空間就是其每點p的局部和 Cn(p)中某開集的一個解析集相同的集合。精確地說,一個豪斯多夫拓撲空間M說是復空間,如果有M的一族開集覆蓋{Uk},對每個k,存在中某開集Ωk的一個解析集Vk及一一連續映射,使得在時,映射是全純映射,即在 Vk的某個領域Ω中存在全純映射 ,使是Fk對Vk的限制。
如果將施泰因流形的定義中複流形M改成復空間M,那就可以照搬過來得到施泰因空間的概念。設M是一個復空間,任取一點x∈M。兩個在x局部全純的函數如果在x的一個更小的鄰域上恆同的話,則稱兩者屬於同一個全純函數的芽。因此,任一定義於M的某開集的全純函數在它的定義域的每一點都惟一確定了一個芽。將M上所有這些局部全純函數的芽合在一起,賦以適當的拓撲,所組成的拓撲空間就稱為M上全純函數的芽層。同樣,可以仿此定義M上光滑函數、連續函數、常數函數等的芽層。若M是複流形,則還可定義(p,q)微分形式等的芽層。概而言之,M上某類函數的芽層在一點的芽就是由所有在該點的局部有定義的該類函數所組成。設U是M的一個開集,F是M上某類函數的芽層。在U的每一點取F在該點的一個芽,所有這些如果可以連續地接成一片,就稱為U上層F的一個截面。事實上,層F在U上的一個截面就是一個在U上定義的該類函數。以層為係數的上同調群就是通過截面來定義的。
任取復空間M的一個開集覆蓋 u={Ui},令,仍是M的一個開集。現設 F是M上的一個層,對每一個,取層Fƒ=()稱為一個k維上鏈。所有k維上鏈組成一個線性空間。在k-1維上鏈和k維上鏈之間可以自然地定義一個映射δ:ƒ→δƒ,
多複變函數論
。
應該指出,這樣定義的上同調群Hk(u,F)依賴於開覆蓋u。但是通過一定的極限手續或對覆蓋中的開集加以適當的規格化,可以使所得上同調群僅與M有關而與具體的開覆蓋 u無關,這樣得到的上同調群就可以合理地稱作M上以層F為係數的上同調群Hk(M,F)。
大體說來,Hk(M,F)是將層F的局部截面“拼接”成整體截面的可能性的一種度量。
以層論為基礎,結合H.嘉當、岡潔等關於全純函數理想論的研究,發展成為疑聚解析層的概念。利用疑聚解析層的理論,H.嘉當、塞爾將全純域的基本理論系統地推廣到施泰因空間上,而得到施泰因空間的基本定理──嘉當定理A與B。前者說,施泰因空間上的任何凝聚解析層在每一點都可由有限個整體截面生成。後者說,對於施泰因空間M上的任何凝聚解析層F,上同調。事實上,嘉當定理 B還可用來定義施泰因空間,即若對復空間M上的任何凝聚解析層F,上同調,那麼M稱為施泰因空間。
黎曼-羅赫定理及其推廣 黎曼-羅赫定理是黎曼曲面理論的基本定理。概括地說,它是研究在閉黎曼曲面上有多少線性無關的亞純函數 (在給定的零點和極點上,其重數滿足一定條件)?所謂閉黎曼曲面,就是緊緻的一維複流形。拓撲上,它相當於球面上連接了若干個柄。柄的個數g是曲面的拓撲不變數,稱為虧格。在閉黎曼面M上取定有限個點αi, 對每一αi附以非零整數ni(ni>0表示ni重零點,ni<0表示|ni|重極點),作形式和D=∑niαi稱為除子,d(D)=∑ni稱為除子D的階數。每個亞純函數ƒ自然具有惟一的除子,記以(ƒ),不僅如此,每一亞純微分ω(亞純微分是M上局部可以表為φ(z)dz的微分式,其中z是局部坐標,φ(z)是z 的亞純函數)也有惟一確定的除子(ω)。利用這一概念,黎曼-羅赫定理可表述為:對於任意給定的除子D,M上存在多少個線性無關的亞純函數ƒ,使ƒ的除子(ƒ)滿足(ƒ)+D≥0?這一線性無關數如果記作l(D),同時記i(D)為M上線性無關的亞純微分ω 的個數,它們滿足(ω)-D ≤0,那麼,著名的黎曼-羅赫定理(1865)可以表為:l(D)-i(D)=d(D)-g+1。例如,取D=0,因而d(D)=0,此時黎曼-羅赫定理給出:M上線性無關的全純微分的個數等於其虧格數。
鑒於黎曼-羅赫定理將復結構與拓撲結構溝通起來的深刻性,如何推廣這一定理到高維的緊複流形自然成為數學家們長期追求的目標。模仿式的推廣是行不通的,例如高維情況下“除子”如何定義就是問題。解決的辦法只能是對黎曼-羅赫定理給以新的說法,使在新說法中出現的各個量可以推廣到高維複流形上去。而這一切只是在層及上同調概念引進並應用於複分析以後才有可能。途徑是這樣的:對M上任何給定的除子D,可以聯繫一個複線叢λ(D)。這一線叢又決定了它的全純截面的芽層。於是,l(D)等於取值於λ(D)的全純截面芽層的0維同調群的維數dimH0(M,λ(D)),i(D)等於dimH1(M,λ(D),d(D)等於線叢λ(D)的陳數(一種表徵拓撲性質的示性數)X(λ(D)),而2(1-g)等於M本身的陳數с(M)。這樣,黎曼-羅赫定理就可以改述成:
塞爾首先注意到這樣的改述。對一般的緊複流形M,設K是M上的復向量叢,以Hq(M,E)表M上取值於K的全純截面芽層的q維上同調群,令。塞爾提出(1953),能否將ⅹ(M,K)用M的陳類及復向叢K的陳類的多項式加以表達?第二年,F.希策布魯赫成功地作到了這一點。他所得到的公式即稱為希策布魯赫-黎曼-羅赫公式。以M上的全純線叢L為例,所得的公式為
式中Tdj是一些與M無關的普適的多項式,稱為托德多項式。
希策布魯赫-黎曼-羅赫公式曾引起了一系列新的研究和推廣。到目前為止,最重要的推廣是阿蒂亞-辛格的指數定理(1962)。M.F.阿蒂亞、I.M.辛格從緊黎曼流形上向量叢間橢圓微分運算元的“指數”的角度,得到了更一般的公式,它是以希策布魯赫-黎曼-羅赫公式為其特例。不僅如此,它還同時統一了其他幾個著名的經典定理,因而被譽為近代數學的重大成就之一。
齊性域與對稱域 Cn中的有界連通開集稱為有界域。單復變的黎曼映射定理說,C 中邊界多於一點的單連通域都全純等價於單位圓|z|<1。多復變的相應問題要遠為複雜,至今離問題的解決還很遠。目前,多復變中對一般有界域的全純分類幾乎沒有什麼結果。研究集中在性質較好的一類:有界齊性域。
設Ω為Cn中的有界域。Ω到自身的雙方一一的全純映射稱為Ω的解析自同構。全體解析自同構在映射的乘法下組成一個群,記作Aut(Ω)。關於Aut(Ω)的結構,第一個基本的結果屬於H.嘉當(1935):Aut(Ω)的包含單位元的連通分支是一個實李群。如果Ω中任何兩點,都存在一個解析自同構將其中一點變成另一點,則Ω稱為齊性的。因為單位圓是齊性的,再加上黎曼映射定理,所以C中任何有界單連通域都是齊性域。多復變中情況就沒有這麼簡單。設Ω是有界齊性域。任意固定其中一點,Aut(Ω)中保持該點不動的解析自同構組成Aut(Ω)的一個子群,記作K。於是,。這樣,就將有界齊性域和李群對其閉子群的商空間聯繫了起來。有界齊性域的研究因而化歸李群的研究。研究李群的代數工具是李代數。李代數就其實質來說,是李群的單參數子群的無窮小生成元。同時,因為Aut(Ω)/K具有齊性的復結構,這就對有界齊性域的李代數賦予了特殊的限制。由此出發,皮亞捷茨基-沙皮羅證明了:任何有界齊性域均解析等價於他所定義的西格爾域。鑒於西格爾域的實現相當明確,這一結果無疑是有界齊性域分類問題的重要進展。
在有界齊性域中研究得最為深入的是對稱域。所謂“對稱”是由單位圓的下述性質抽象出來的:對於|z|<1,存在解析自同構 g:z→-z。這一映射只以O為不動點,且將通過Ο的所有測地線都反轉了過來。有界齊性域Ω,如果對任意的,都存在g∈Aut(Ω),滿足:①,且z是g的惟一不動點;②g2=1,則Ω稱為對稱域。顯然,對稱域是有界齊性域中與單位圓更相近似者。將對稱域在解析等價意義下加以分類,是É.嘉當的重大貢獻(1936)。他利用他首創的黎曼對稱空間的理論,給出了對稱域分類的完整結果:任何對稱域都是一些既約對稱域的拓撲積。而既約對稱域共四大類,外加兩個例外域(其復維數分別是16和27)。前四大類對稱域中國數學家華羅庚稱之為典型域。如果用矩陣實現,它們是:
。
。
。
多復變的自守函數 設Ω是Cn中的有界域。Ω的全體解析自同構組成群Aut(Ω)。Aut(Ω)的子群Γ稱為不連續的,如果對於Ω中的任何點x,都存在一個領域U,使得Γ中僅有有限個元素σ,使σ(U )和U 相交。所謂自守函數就是相對於某個不連續子群Γ而言的。相對Γ的自守函數,指的是定義於Ω的亞純函數,它在Γ下不變,即對任何x∈Ω和任何。在自守函數的研究中,一個主要的概念是基本域。如果Γ是一個不連續子群,那麼Ω在 Γ的作用下分成一個個互不相交的“軌道”Γx。以這些軌道為元素組成的空間Ω/Γ稱為Γ的基本域。基本域具有自然的拓撲結構,一般是一復空間。自守函數因為在Γ下不變,它自然可以看成基本域上的亞純函數。早在19世紀末,龐加萊就提出了一套如何構造自守函數的有效方法。他用無窮級數首先構造自守形式,再由自守形式的商求得自守函數。這種級數後人稱之為龐加萊級數。所得自守形式,是定義於Ω上的全純函數ƒ,滿足對任何σ∈Γ,有。這裡jσ(z)稱為自守因子,是Ω上的亞純函數,其特徵性質為:對於任何σ,τ∈Γ有:。顯然,對應於同一自守因子的兩自守形式之商自然是一個自守函數。自守函數論中最常用的自守因子是以下形式:,其中是映射σ的函數行列式。自守函數論的中心問題是研究自守函數組成的域的代數結構。20世紀中葉以前,這方面的主要貢獻屬於西格爾。在基本域緊緻的情況下,西格爾證明了:任一自守函數都可以寫成自守形式之商;任意n+1個自守函數都是代數相關的;可以選擇n+1個自守函數ƒ0,ƒ1,…,ƒn,使任何自守函數都能表成它們的有理函數。此外,西格爾依據他對二次型的解析理論的出色研究,構造了一大批具有重要意義的基本域的例子(緊緻的和非緊緻的)。這些例子都與代數群的算術子群密切相關。50年代以後,自守函數研究的重點轉向基本域非緊但體積有限的情況。這方面,隨著賽爾伯格“求跡公式”的提出,蓋爾范德、朗蘭茲等人揭示了自守函數與李群的無窮維表示、代數數論等的內在聯繫,引起了大量的深入研究。時至今日,這一領域正處於近代數學的眾多分支:複分析、代數幾何、代數群、代數數論、李群等的交匯點,其重要性正與日俱增。